3. 通信中的概率-1
3.1 通信系统中离散随机事件的建模
离散随机变量表示通信系统中发生的一种行为,其结果并非绝对确定。例如,二进制信息源下一步产生的值可能是两个输出之一:二进制1或二进制0。 尽管我们知道两种取值均可能出现,但并不确定二进制信息源的输出中具体会产生哪一种取值。
因此,我们将二进制信息源可能产生的输出值建模为随机变量。之所以称该随机变量为离散随机变量,是因为它从有限的选项中产生单一可能的输出值。
为了用数学方法描述该离散随机变量,假设定义X,使其存在一组不同的实数x_{i} ,且该变量能产生这些值中的每一个,且各自具有具体的发生概率:

其中P(X=x_{i})表示随机变量产生输出值x_{i}的概率。根据全概率法则[1],我们有
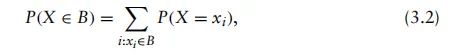
集合B由一组值xi组成。离散随机变量的一种特定形式是整数值随机变量,其输出值为整数xi=i;即,
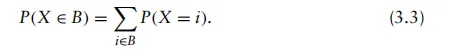
由于随机变量X的每个输出具有不同的出现概率,我们通常将特定离散输出xi由X生成的概率定义为

式中,pX(xi)称为概率质量函数(PMF)。 注意,PMF的取值受以下约束
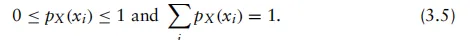
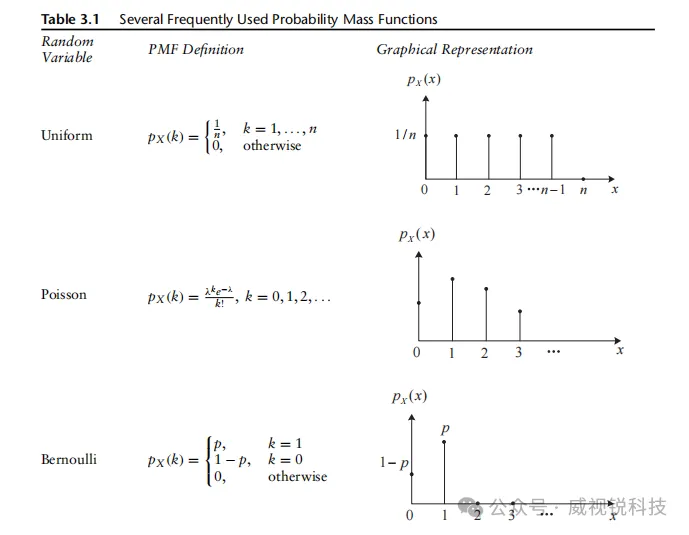
表3.1列举了几种常用的PMF,包括均匀分布、泊松分布和伯努利分布。特别地,伯努利随机变量用于生成二进制信息源的随机输出,而泊松随机变量常用于建模计算机网络中路由数据包的延迟。
现探讨如何利用这些离散随机变量来模拟通信系统的实际组成部分;即二进制信息源。该工具需包含一个关键特性,即随机数生成器(RNG)产生的1与0的比例。在代码3.1的MATLAB脚本中,实现了一个二进制RNG,该脚本生成三个向量。向量b1包含一和零的数量均等,而向量b2和b3分别产生一和零比例为60/40和20/80。注意,MATLAB中的均匀随机数生成器函数rand用于生成介于零和一之间的随机值,随后将其四舍五入至最接近的整数,即一或零。

通过操作输出值及rand命令,将其四舍五入为零或一,并偏置所有值使其更接近一端或另一端,我们可以生成具有不同比例一和零的二进制随机值,如图3.1所示。利用stem命令,可以可视化图3.1(a)、图3.1(c)和图3.1(e)中显示的实际二进制值。尽管这为我们对这些二进制随机数生成器的行为提供了总体观察,但很难区分向量中一和零的具体比例。因此,利用直方图和一组非常长的随机生成值序列,我们可以对这些比例进行准确刻画,如图3.1(b)、图3.1(d)和图3.1(f)所示。请注意,直方图准确地反映了输出向量中一和零的比例分布。一个重要的注意事项:由于我们的刻画依赖于对随机现象的观测,您需要观察大量数据才能准确地对其进行刻画。
3.1.1 期望
由于我们无法确切获知构成通信系统及其环境的这些随机现象的输出值,因此必须采用数学方式刻画这些随机变量的统计行为。刻画随机变量的一种方法是其期望值或均值,该值可通过下列表达式定量计算
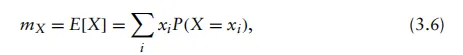
其中,每个取值按照其发生概率加权求和。因此,利用概率质量函数的定义,我们可以将式(3.6)改写为

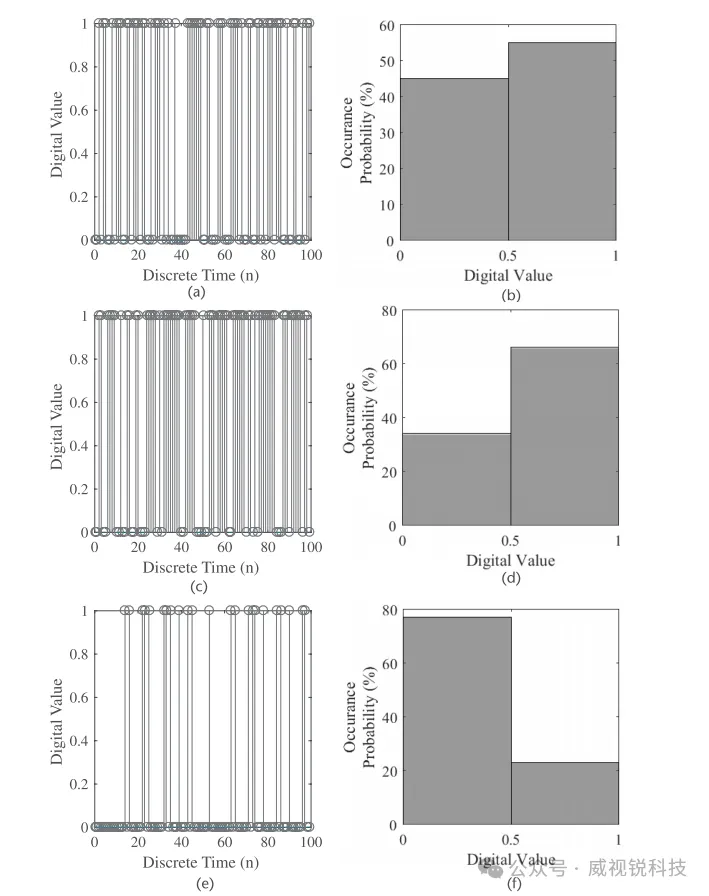
图3.1三个二进制传输的干图和直方图,它们分别具有不同的1和0出现概率。(a) 二进制信号(1占50%,0占50%),(b) 直方图(1占50%,0占50%),(c) 二进制信号(1占60%,0占40%),(d) 直方图(1占60%,0占40%),(e) 二进制信号(1占20%,0占80%),(f) 直方图(1占20%,0占80%)
假设我们有一个随机变量X和一个实值函数g(x),它将其映射为一个新的随机变量Z,即Z=g(X)。 由于X实际上是将样本空间中的点映射到一组实数,因此在求解随机变量Z时,实际上是在对一个映射进行映射;因此,为了计算随机变量Z的期望值,即E[Z],可以采用以下表达式:
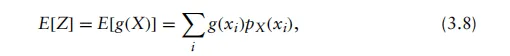
这称为随机变量函数的期望。(3.8)的一个最重要方面是, Z的期望可以利用 X的概率质量函数(PMF)求解,无需确定Z的概率质量函数。表3.2列出了与期望算符相关的若干重要性质。

3.2 二进制通信信道与条件概率
在数字通信系统中,我们可以将接收机的操作视为在观测到接收端的随机变量Y后,尝试猜测由特定发射机发送的传输值X,该传输值可被建模为随机变量。因此,我们需要某种判决规则来确定 X的原始传输值。如图3.2所示,X可输出值0或1,而Y则在接收机处被观测。注意,观测值Y可能被误判为非传输值;即X=Y。
为了描述和理解该随机传输环境,我们可以采用条件概率的定义,其数学表达式为
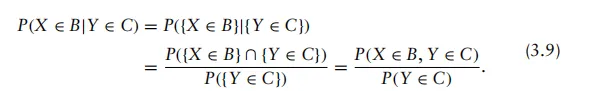
此外,条件概率质量函数(PMF)也可用于数学描述该随机现象:

其后可表达为
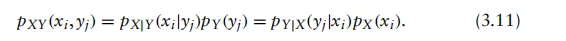
一个可用于刻画由条件概率和/或条件概率质量函数描述的现象的重要数学工具是全概率法则。例如,设Y为任意随机变量,取A={Y∈C},其中C⊂R。 因此,我们可以定义
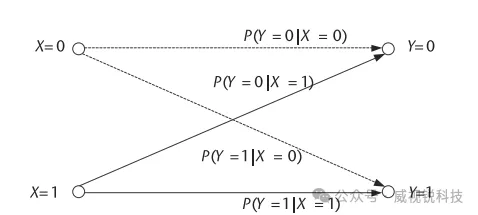

图3.2二进制信道示例,其中随机变量X生成的传输值被接收机以随机变量Y的形式观测
全概率法则表示为
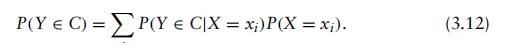
类似地,如果Y是一个离散随机变量,取不同的值yi,并设 、C= {yi},则可得、出以下全概率法则:

回到图3.2所示的二元通信信道模型,假设我们希望根据截获的接收信号观测值来判定传输值。在此情况下,我们采用最大后验概率(MAP)判决规则,即在观测到Y=j时,MAP规则指出应判定X=1,当且仅当
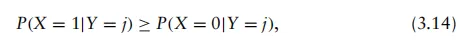
并据此决定X=0,否则。换言之,MAP规则在观测到Y=j的条件下,若X=1的后验概率大于X=0的后验概率,则判决为X=1。 此外,我们可以观察到
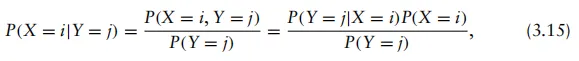
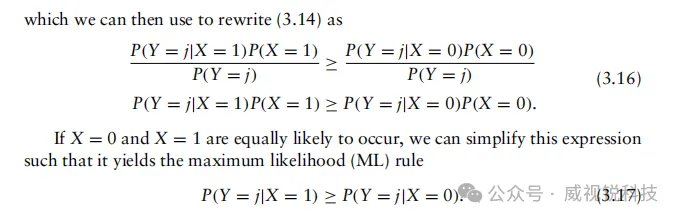

此外,在一般情况下,我们可以重新排列(3.16),使其得出似然比,即:
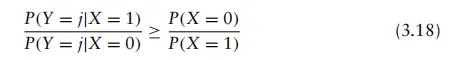
其中右侧称为阈值,因为它不依赖于j。
基于该数学表达式,现通过计算机仿真对同一示例进行分析。使用如下MATLAB脚本,我们可以模拟一个二进制信道,生成L个二进制值,其中值为1的概率为prob4,剩余为0。 此外,假设所用二进制信道非对称,即1值翻转为0值的概率与0值翻转为1值的概率不同。请注意,位值翻转被视为信道产生的误差。因此,我们定义传输的1值被正确接收为1值的概率为prob11,传输的0值被正确接收为0值的概率为prob00。
评估任何数字通信系统性能的基础度量之一是比特误码概率,或称位误差率(BER)。BER表征接收的位错误相对于传输的总位数的比例。针对不同应用,会考虑不同的BER值。
可接受,而其他则被视为不可容忍。例如,对于典型的无线数据传输应用,误码率10−5被视为传输中可接受的误差量。
在上述涉及二进制信道的MATLAB示例中,我们希望对BER值进行表征,以验证其是否符合我们定义的参数。图3.3展示了整体传输的BER,以及仅针对1值和0值传输的BER。 请注意,仅针对1值的BER对应概率prob11的补集,针对0值的BER同样对应概率prob00的补集。请记住,为了获得误码率的准确统计评估,需要生成大量二进制值。
文章来源:威视锐科技