特性
本文涵盖以下主题:
实现算术函数的并行与串行方法比较
基础串行乘法与加法的构建模块
采用串行逻辑的整数多项式实现方案
可变多项式阶数与数据位宽
测试平台示例
简介
在先前的文章中,我探讨了运用霍纳法则和定点逻辑来减少多项式计算所需时钟周期的优势。本文将介绍一种截然不同的方法——采用串行逻辑替代并行逻辑,虽然需要更多时钟周期,但能显著减少面积占用并可能获得更高时钟频率。在多数现代设计中,速度和功耗比面积更受关注,但在特定场景下串行逻辑仍具考量价值。另请注意,本设计采用全精度整数运算,而非首篇文章中的定点运算。
霍纳法则
与前文相同,本文仍采用霍纳法则来减少所需乘法运算次数。假设我们有以下形式的n 阶 多项式
f(x) =anxn + an-1xn-1 + … +a1x + a0.
直接计算该形式需要总共 n(n+1)/2 次乘法和 n 次加法,使得计算复杂度达到O(n2).。
霍纳法则指出,我们可以将其因式分解并改写为:
f(x) =(((anx + an-1)x + an-2)x + an-3)x + … )x +a0.
使用这种形式可将所需操作减少至n 次乘法和n 次加法。计算复杂度现在降至O(n) ,使得高阶多项式更易处理。
由于多项式是乘法与加法的组合,本设计中的两个主要构建模块正是这两种运算的串行版本。最基础简单的模块是加法器。
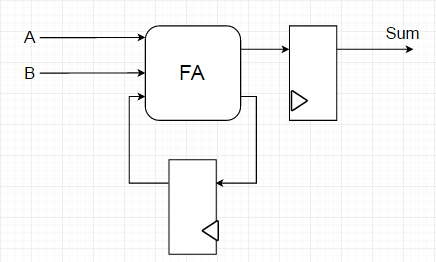
图 1 .串行加法器示意图。
串行加法器本质上是一个全加器,其进位端带有反馈触发器,输出端也配有触发器。因此,若A为M 位、B为N 位,则完整加法运算需消耗max(M,N) 个时钟周期。

图 2 .4位串行乘法器示例。
该图展示了串行/并行乘法器的4位实例。其中一个输入为并行信号并存储在寄存器中,另一个则是按位串行提供的单比特信号。与门生成部分积,这些部分积与前级输出共同输入加法器。每个加法器的进位输出通过触发器反馈至其进位输入端。运算时从第0位开始向左推进,对部分积与进位构成的列求和,结果位锁存至输出触发器。对于位宽为M 的被乘数和位宽为N 的乘数,完整乘法需M+N 个时钟周期。
本设计中额外添加了处理负数的逻辑电路。若被乘数为负,则先取其正值,最终结果再取反。这确保结果总能正确进行符号扩展。
乘法器与加法器组合成更高层的乘加模块,用于实现Ax+B运算。需额外配置触发器来延迟B输入,使其在正确时刻到达加法器。
顶层设计中,串行多项式模块包含若干乘加模块(数量等于多项式阶数)、输入输出移位寄存器,以及控制数据流的状态机。图3展示了三阶多项式数据通路的简化视图,省略了部分控制信号。注意粗线代表总线,普通线代表单比特信号。
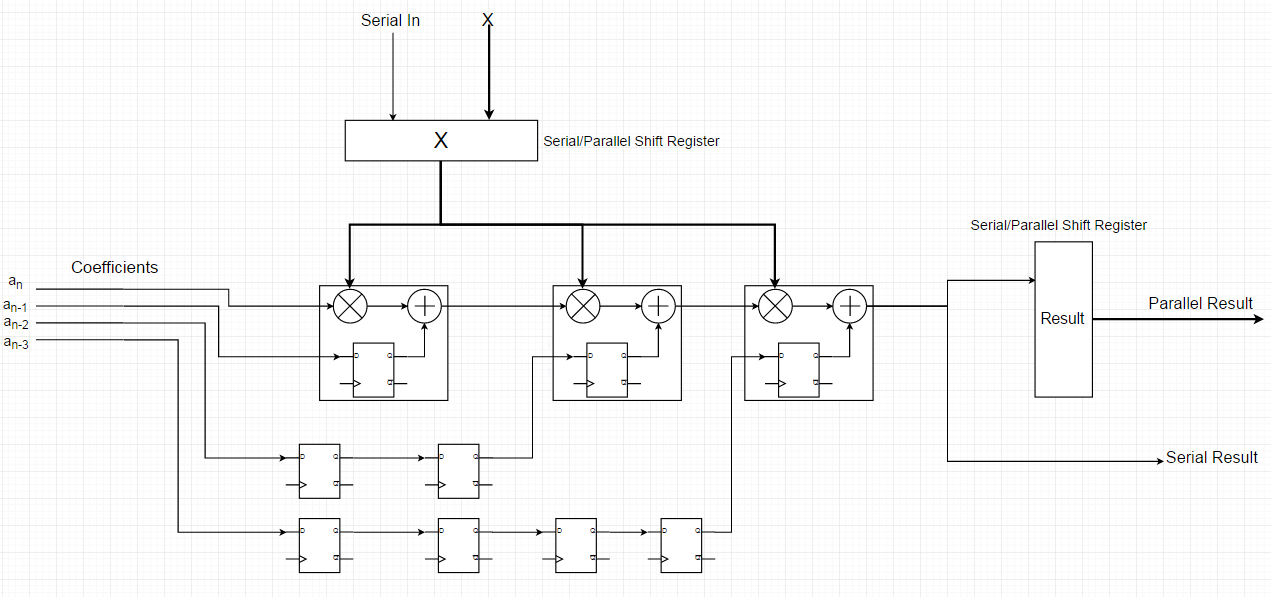
图 3 .串行多项式模块的顶层视图。
该多项式模块有两个通用参数:输入数据宽度和所实现多项式的阶数。
输入移位寄存器有两种加载选项,可通过s_p信号切换。若s_p为高电平,X寄存器将通过shift_X端口串行加载。当s_p为低电平时,X将在下一个时钟上升沿并行加载。
coeffs 向量为每个系数包含一个位,其中coeffs(0) 是an的串行线,coeffs(1) 是an-1的串行线,以此类推。从 an-2开始,每个系数在输入与加法器之间增加两个触发器,后续每个系数再额外增加两个。这延迟了信号,使其在正确时间到达对应模块。这些触发器由主时钟信号的反相版本驱动,以最大化后续阶段的建立和保持时间。
输出端结果可从shift_out端口或并行结果端口获取。每个端口都有对应的标志信号,用于向外部主机提示计算完成。当shift_out持有结果的LSB时Valid信号置位,并保持高电平直至计算结束。当完整结果载入输出移位寄存器时Done信号置位,并在下次计算开始时撤销。
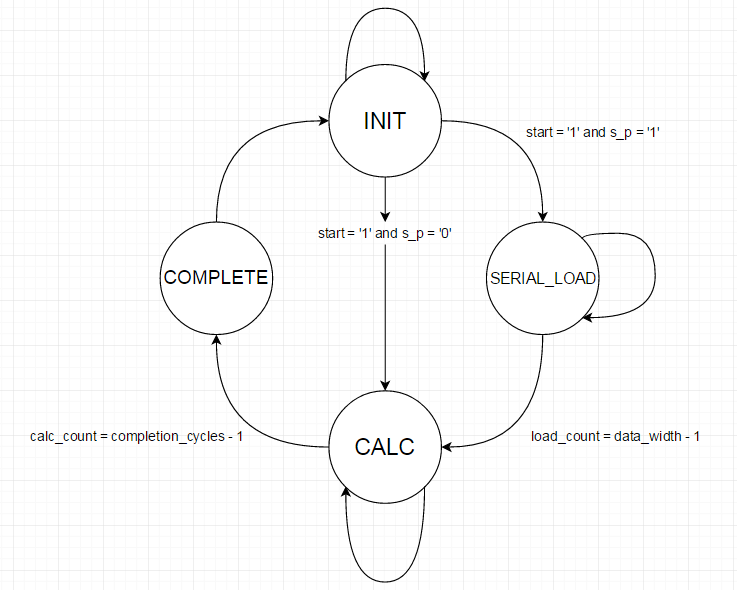
图 4 .状态机示意图。
上述状态机用于控制计算流程。在INIT状态,X输入总线上的数据被锁存到寄存器。若使用串行模式,则锁存shift_X上的数据。所有其他控制信号均设置为初始条件。
当start信号变高后,状态机可转入SERIAL_LOAD状态或CALC状态。若选择串行模式,则进入SERIAL_LOAD状态——此时数学运算部分禁用,X的剩余位被移入输入移位寄存器。当该过程完成,或INIT状态选择了并行模式时,状态转为CALC。
CALC状态是数学运算开始的阶段。链式结构中的首个乘加模块被启用,同时输入移位寄存器被禁用。在此状态下,时钟周期被计数并用于启用乘加模块和输出寄存器。由于乘加操作需要两个时钟周期,链中下一个模块会在前一个模块启用后两个时钟周期被激活,直至所有模块均启用完毕。经过2*多项式阶数次时钟周期后,计算结果的首位(最低有效位)得以生成。此时输出移位寄存器被激活,最终结果开始逐位移入。
下方时序图展示了四阶多项式配合四位数据宽度时,各阶段结果可用的时间节点。注意当某阶段最后一位计算完成后(阶段1,周期10-11),后续所有位均为结果的符号扩展。
图 5.计算过程时序图。
再经过 (poly_order+1)*data_width 次时钟周期后,最终结果的最高有效位完成计算并移入输出寄存器。随后输出寄存器被禁用,状态转为完成(COMPLETE)。
在完成((COMPLETE))状态下,结束标志位被置位,状态机返回初始状态以开启新计算。
至此应当明确,该方法比传统并行方式需要更多时钟周期。由此产生合理疑问:若此方法速度明显更慢,为何仍有人采用?答案在于资源占用。下表对比了Quartus对串行与并行拓扑结构下乘加模块的综合结果。并行版本采用Altera库中的IP核实现,针对Cyclone V SoC进行默认优化。
表 1 .自适应逻辑模块(ALM)资源占用情况。
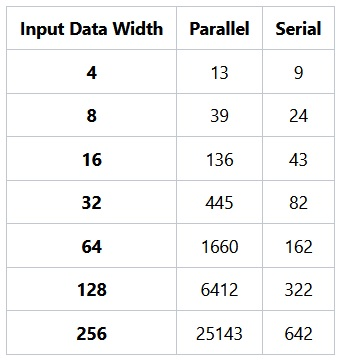
虽然低数据位宽时并行与串行资源占用相近,但并行方案成本随位宽呈二次方增长。不过由于多数FPGA芯片内置硬件乘法器,通常无需使用逻辑元件构建乘法器。
串行实现方案随数据位宽线性增长。但这仅适用于对延迟不敏感的场景。并行乘加最低延迟为一个时钟周期,而此串行方法的最低延迟为乘积位宽加一个周期。例如,一个32位串行乘加运算需要65个时钟周期。
串行方法是一种有趣但小众的解决方案。在通过串行协议从外部主机接收数据的情况下,这种方法可能很有用。这种情况下,数据可以随到随处理,而无需等待整个传输完成。其他以面积为主要考量且不关心延迟的场景,也可以考虑采用串行方法。
仿真与测试
本设计在ModelSim中进行了仿真。示例测试平台包含四组随机选择的系数值。前三组使用并行加载模式,最后一组采用串行加载模式。
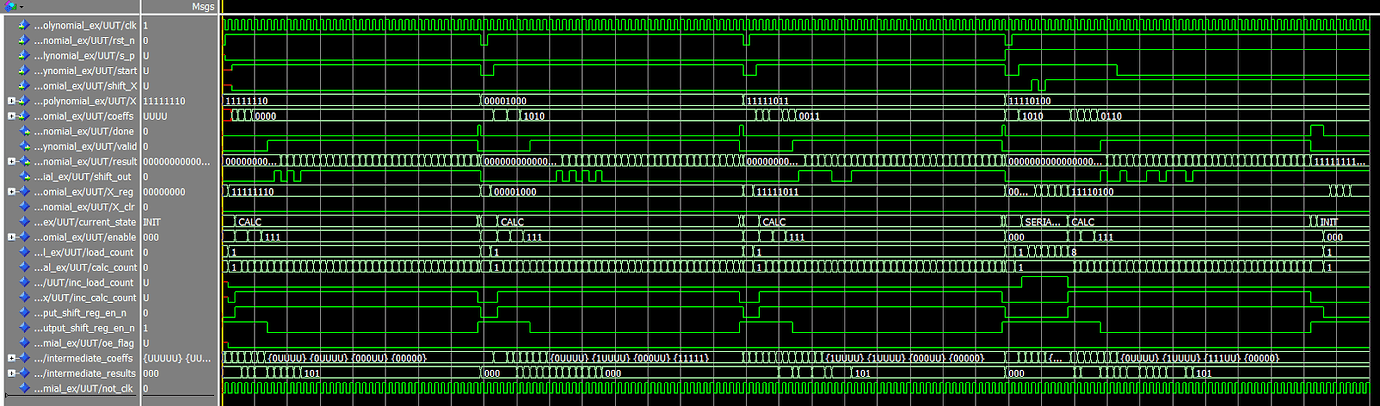
图 6 .仿真屏幕截图。
当资源缩减至关重要而延迟不成问题时,串行算术是一个可行的选择。因此虽然适用场景有限,但仍是一个值得了解的替代方案。由于多项式在工程领域无处不在,这是用串行构建模块创建高级函数的一个良好起点示例。
该概念的潜在扩展可包括应用于浮点数或定点数。整个多项式设计也可能被改进为全流水线结构,以更高效地处理连续计算。
该.zip文件包含项目所有VHDL源文件,包括顶层测试平台和仿真用.do文件。
Serial Polynomial_v1.1.zip (13.0 KB)