4.6 最优检测
检测理论,又称信号检测理论,用于区分信号与噪声[2]。 基于该理论,我们能够说明改变判决阈值如何影响区分两种或多种情况的能力,常揭示系统对特定任务、目的或目标的适应性。
4.6.1 信号向量框架
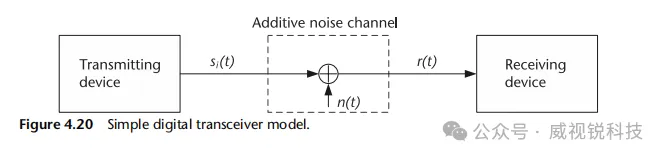
我们假设如图4.20所示的一个简单数字收发器模型。如前所述,接收机只能观测到被噪声信号n(t)损坏的si(t),即r(t)。噪声信号n(t)通常表示所有噪声源的综合为单一变量。因此,检测问题可归纳如下:给定0≤t≤T区间内的截获信号r(t),判断哪一个si(t),i=1, 2, ...., M,存在于该截获信号中。
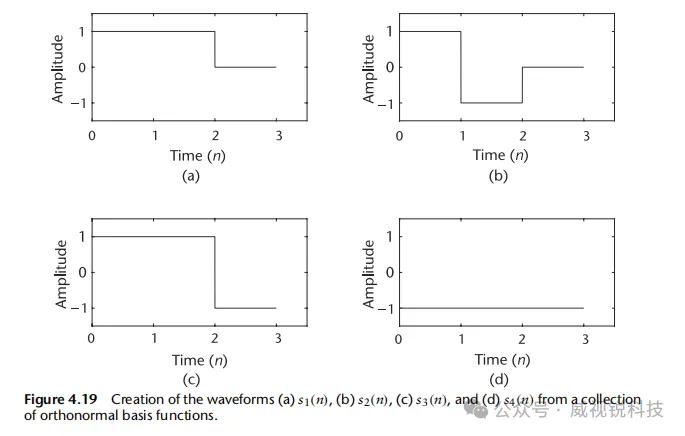
假设我们将波形si(t)、噪声n(t)和截获信号r(t)分解为施加于一组正交归一基函数上的权重集合,即:
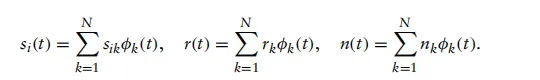
鉴于所有这些信号波形均使用相同的正交归一基函数,我们可以将波形模型表达式r(t)=si(t)+n(t)重写为
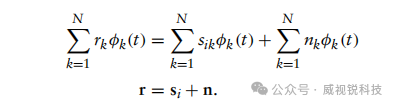
由于r由确定性波形si与概率信号n的组合构成,我们现将注意力转向对n的数学刻画。鉴于噪声信号n(t)假设为高斯随机变量,需确定该随机变量的特性如何转化为信号。
向量表示。我们知道噪声向量元素nk等于

它是噪声信号波形在标准正交基函数φk(t)上的投影。由于噪声信号n(t)是高斯随机变量,且积分过程为线性运算,因此nk也是高斯随机变量。因此,噪声信号向量n是高斯向量。现着手确定噪声向量n的统计特性,以便应用于信号波形检测。
首先,我们计算这些向量元素的均值。由期望的定义可得
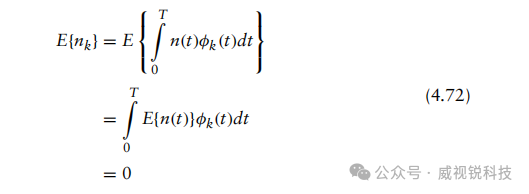
由于E{n(t)}=0,这意味着噪声信号向量的均值为E{n}=0。

求解E{nknl}得到
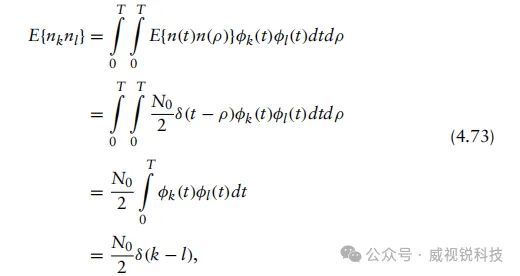
两个正交归一函数φk(t)与φl(t)乘积的积分结果是一个德尔塔函数,因为仅当k=l时,这两个函数才会相互投影。因此,该结果的矩阵等价形式为

鉴于(4.74)中获得的高斯随机变量的向量表示,我们需要定义该表示的联合概率密度函数,以刻画该向量的各个元素。基于噪声元素相互独立的假设,我们可以将联合概率密度函数表示为各元素概率密度函数的乘积,从而得到

4.6.2 判决规则
依据(4.76)式中推导的联合概率密度函数,我们现在可以为接收机制定一条规则,用于判定在信道噪声存在的情况下所截获的信号波形。假设我们为接收机定义如下判据:
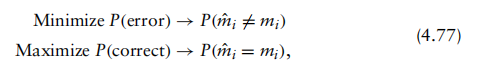
其中误差概率为P(e)=P(误差),正确接收概率为P(c)=P(正确),且P(e)=1−P(c)是这两个概率间的互补关系。然后,利用全概率法则,整体正确判决概率为
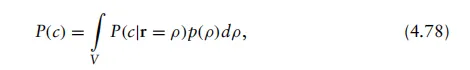
where P(c|r=ρ) ≥0 and p(ρ) ≥0. 因此可以观察到,当P(c)达到最大值时,P(c|r=ρ)也必然达到最大值。
为了最大化P(c|r=ρ),接收机应采用以下判决规则:
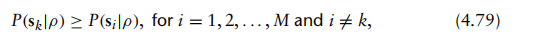
其中i=1, 2,...,M且i≠k。 注意,对于此判决规则,我们假设sk存在于ρ中,即

采用由概率密度函数与概率组成的混合型贝叶斯定理,即
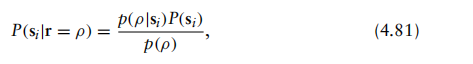
我们希望将该判决规则转化为接收机能够应用的表达形式。具体而言,回顾本节前面我们欲最大化的量P(c|r=ρ)。 通过采用混合贝叶斯定理的表达式,最优探测器可以重写为
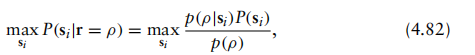
对于i=1, 2,...,M。 由于p(ρ)不依赖于si,故可简化最优探测器表达式为
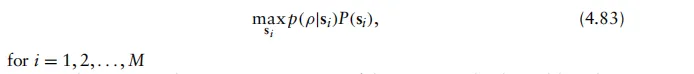
基于(4.83)的结果,可依据该表达式推导出两类探测器。第一类探测器称为MAP探测器,其表达式为
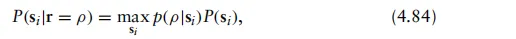
对于i=1, 2,...,M。然而,若P(si)=M1,表明P(si)不依赖于si,则可将P(si)项从最优探测器表达式中省略,从而得到第二类探测器,称为最大似然(ML)探测器:

对于i=1, 2,...,M。 在下一节中,我们将基于数据传输通过加性高斯白噪声信道时的最优判决规则,数学推导最大似然探测器。
4.6.3 加性高斯白噪声信道中的最大似然检测
最大似然检测是一种常用的统计方法,用于将统计模型拟合于数据,并识别模型参数。一般而言,对于固定数据集和潜在概率模型,最大似然方法选择能够使观测数据的分布概率最大化的模型参数值(即最大化似然函数的参数)。
假设一段数据传输正在通过加性高斯白噪声信道进行,在被接收机截获之前。回顾该场景的传输模型表示为

其中si是由发射机发送的第i个信号波形,n是加性高斯白噪声信道引入的数据传输噪声,r是被接收机截获的信号波形。鉴于si是确定性量,而n是一个刚通过联合概率密度函数描述的随机量,现需对r进行描述,该描述可由n的描述结合si的确定性特性推导而得。
假设我们考虑接收向量中某单个元素的条件概率,即在假定信号波形si已被传输的条件下,接收向量r=ρ中第k个元素的条件概率:
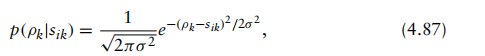
其中噪声向量的第k个元素为nk=ρk−sik。 由于假设加性高斯白噪声向量元素相互无关(即独立),因此该条件概率表达式可以改写为
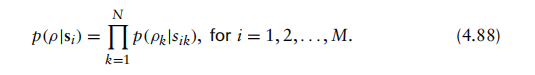
因此,该多个基本概率密度函数的乘积最终导出以下表达式:
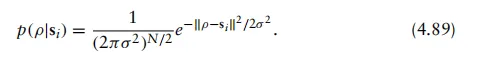
请注意,我们现在得到的条件概率表达式完全由si,ρ及其相应元素表示。利用该表达式,我们可以继续数学推导最大似然探测器。
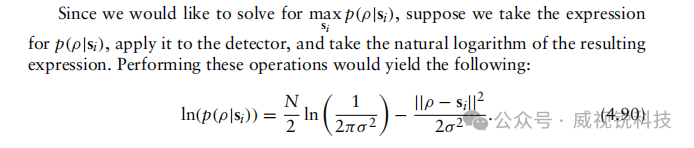
注意,采用自然对数是为了去除表达式中的指数基,使最优判决规则的表达式线性化。此外,因自然对数为单调函数(即若x2 ≥ x1则ln(x2) ≥ ln(x1)),判决规则中使用不等式依然有效。
通过求解此线性判决规则,并结合自然对数的单调性,我们可以推导出以下结论:
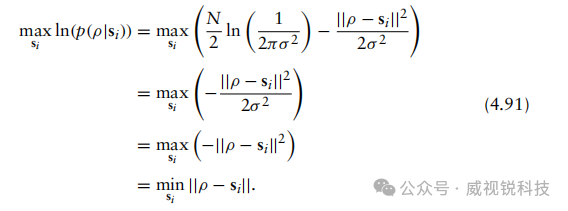
鉴于我们关注的是使判决规则取得最大值的选取si,故可将该判决规则重写为
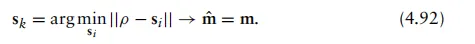
值得注意的是,采用向量表示法处理这些判决规则的一个优势在于,整个情形均可用距离加以诠释。具体而言,量||ρ − si||实际上表示两个向量ho和si的向量首端之间的距离,且这两个向量的尾端均位于原点。因此,最大似然探测器相当于最小距离探测器。