本文涵盖以下主题:
基于霍纳法则在FPGA中实现多项式运算
采用定点数格式的分数运算
与外部处理器的接口设计
可扩展的多项式阶数与数据位宽
基于MATLAB的测试平台与验证
在处理器上计算高阶多项式可能极其耗时。例如,未经优化时10阶多项式需要65次乘法和10次加法。假设每次运算仅需1个时钟周期(实际往往更长),处理器至少需要75个周期才能完成计算。本设计采用两种方法缩短计算时间:时钟周期数仅需多项式阶数加2,即每个输入对应1个周期。首先,霍纳法则能以更少的乘法次数完成多项式计算。其次,采用定点数而非浮点数也能减少乘法运算所需时间。
霍纳法则
本设计的核心是霍纳法则——一种高效简洁的多项式计算算法。假设存在如下形式的n阶多项式
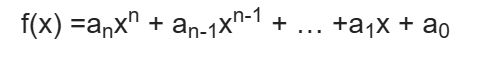
直接计算该式需要进行 n(n +1)/2 次乘法和 n 次加法 ,时间复杂度为 O(n2) 。
霍纳法则通过因式分解将多项式改写为:
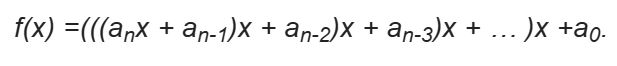
使用此形式可将所需操作次数减少至 n 次乘法 和 n 次加法。计算复杂度现在降至 O(n) ,使得高阶多项式更易处理。
在此应用中,多项式输入和系数以定点格式表示。定点数本质上是一个普通二进制整数,在此情况下被解释为小数。将采用Qm.n 表示法,其中m为整数位数(不包括符号位),n为小数位数。最终数据宽度为m+n+1位。请注意,某些情况下会将符号位计入 m ,使总宽度变为 m+n 位。只要保持一致性,两种约定均可使用。本文遵循第一种约定。还需注意这些参数在多项式VHDL代码中可作为泛型使用。例如,Q3.4数字为8位宽,包含1位符号位、3位有符号整数部分和4位小数部分。但在许多情况下,m 为0,除符号位外所有位都分配给小数部分。
与浮点数不同,定点数的小数点是隐含的,需要设计者在计算过程中自行跟踪小数点位置。定点数的动态范围[-(2m), 2m - 2-n]也远小于浮点数。优势在于它不需要特殊硬件,因为数字是常规整数,计算速度更快。数字分辨率2-n在整个动态范围内保持恒定。
由于定点数是整数,其算术运算与任何二进制补码数基本相同。需要注意的是,在进行Q数加减时,用户必须保持小数点对齐。可通过移位小数位差或直接在HDL中指定正确位来实现对齐。进行加减运算时还需注意溢出问题。在某些情况下,如果系统整体增益能使数值保持在允许范围内,可以允许溢出。若中间计算会使数值回绕至正确结果,也可允许溢出。
Qm1.n1 数与Qm2.n2 数相乘将得到Q(m1 + m2).(n1 + n2) 数。注意两个最高有效位始终相同,因为它们分别是符号位及其一位扩展。乘法运算同样可能发生溢出,但由于一个或两个操作数通常会被归一化为0到1之间的幅度,因此这通常不是问题。
多项式
霍纳法则已证明,多项式可以通过形如 a1x + a0的一阶多项式分段计算* 。因此该设计最基本的构建模块是乘法器和加法器。这些组件的VHDL代码可在adder.vhd和mult.vhd中找到。
乘法器直接使用VHDL内置的有符号乘法函数,并带有寄存器输出。这样,如果FPGA内置乘法器模块,就应该能利用它们。加法器采用无寄存器输出的先行进位架构。
这两个构建模块被组合成一个更高层次的模块,在mult_add.vhd中执行单次乘加运算。该单元实现函数 a1x + a0,其中 ai 和 x 都是Qm.n格式的数值,用于霍纳法则的每个阶段。因此n 阶多项式需要n 个该模块的实例。
假设系数、输入x或两者都被归一化为0到1之间的幅度,这样乘法结果可以存回相同数据大小,因为整数位不会溢出。在本应用中,乘法结果会被直接截断,取符号位、小数点左侧最近的 m 位和小数点后前 n 位 。
这是整数和小数长度首次发挥作用的地方,因为需要在正确位置截断结果以保持正确格式。单独的乘法器和加法器只处理整数,不关心小数点位置。

图 1. 多项式RTL视图。
在多项式层级,乘加模块级联排列,使一个模块的结果输入到下一个模块。上图图1展示了一个三阶多项式模块的RTL视图。该层级还为x和每个系数添加了寄存器。这样可以使用单一总线连接所有输入。内部信号在每个时钟上升沿移位,将输入载入各自的寄存器。数据必须按x、 an, an-1, …, a0的顺序排列。最终结果将在n+2 个时钟周期加上加法器传播延迟后有效。*
以上就是多项式模块的内部工作原理。不过,这个设计最初的构想是将其作为主控微处理器的协处理器使用。当应用于片上系统(SoC)时,该设计能充分发挥优势——处理器和FPGA架构可通过内存映射寄存器共享数据。但本指南旨在提供通用方案,应适用于您现有的任何硬件设备。
外部MCU本可采用并行接口直接连接多项式模块,但这会占用大量引脚。串行接口可能更实用,因为几乎所有MCU都内置了该接口。本示例采用基于此文档实现的SPI从机接口。顶层测试平台也整合了此文档中的SPI主机模块。虽然SPI是常见串行接口中最快的,但任何串行接口都会造成显著瓶颈——尤其在高阶多项式和大数据位宽场景下。若需快速获取结果,这就成了问题。建议用户根据需求开发定制接口(如前文所述的内存映射方案),并与多项式模块结合使用。
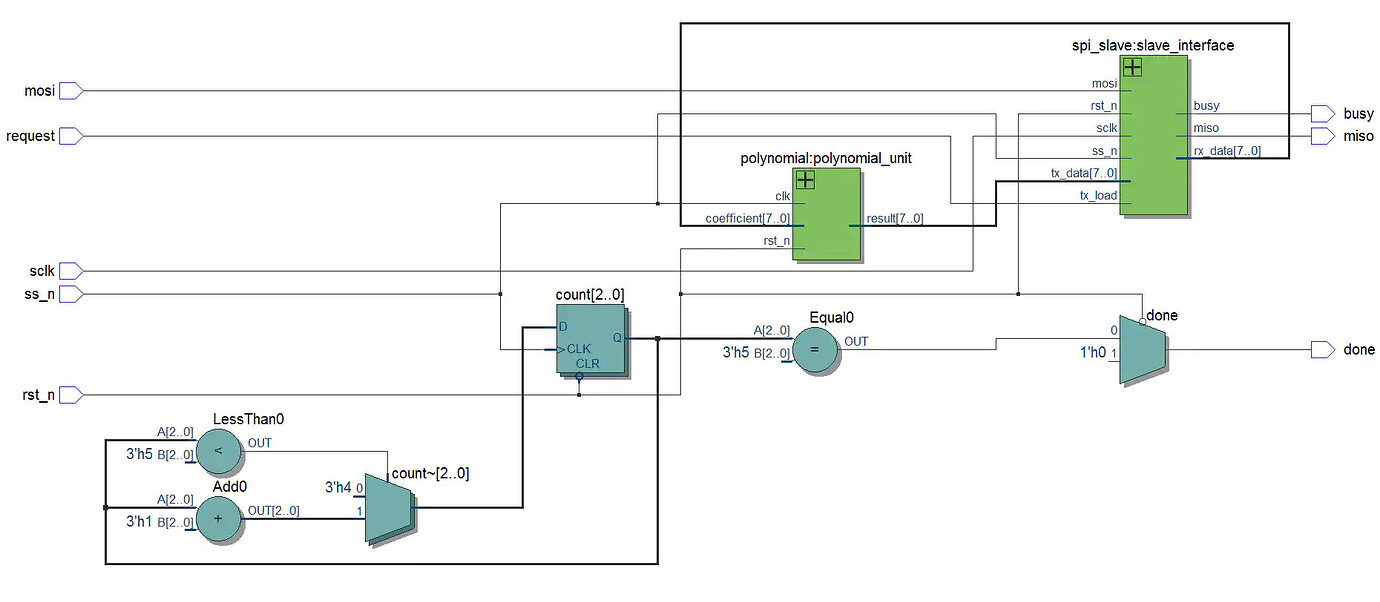
图 2. 顶层RTL视图
图2展示了包含SPI接口的顶层设计。该SPI接口将片选信号作为多项式单元的时钟,在事务完成时锁存数据,从而实现数据实时处理。计数器记录事务数量,最终计算完成后通过置位"done"输出信号通知主机。主机随后在下次SPI事务开始时触发"request"信号线,结果将在该事务期间被锁存并返回主机。从机将在同一事务中等待下一个x值以启动新计算。注意本应用仅使用SPI模式3。
本设计采用ModelSim Altera Starter Edition v10.4b进行仿真。测试数据通过Matlab的fi函数生成。Matlab脚本运行相同算法并输出预期结果用于比对。首次仿真仅测试多项式单元。测试数据采用Q7.24数据格式的七阶多项式,因此数值范围在-128至128-2-24之间。但为避免溢出,实际选用数值范围调整为-64至 64-2-24。

图 3. ModelSim中的多项式模块仿真。
第二次仿真整合了SPI接口,并使用更常见的Q0.15数据格式计算三阶多项式。
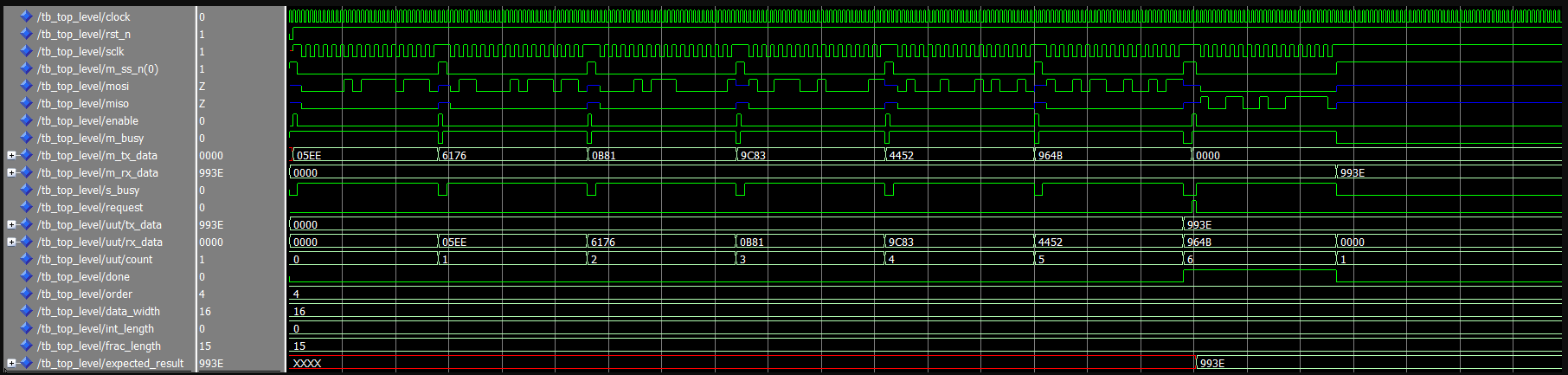
图 4 。 ModelSim中的顶层设计仿真
下载包中包含Matlab脚本与测试平台文件。需注意根据Matlab采用的舍入方法不同,仿真结果可能存在微小差异。本应用采用的直接截断方式等效于Matlab的"Floor"舍入法。
该设计实现了霍纳法则,支持可变阶数、数据位宽及整数/小数长度的定点数多项式运算。用户可随时将现有乘法器/加法器组件替换为其他硅片供应商的IP核。示例中采用SPI接口与主控微处理器通信,但这并非最优方案,建议用户根据应用需求设计专用通信接口。
下载文件
Polynomial.zip (17.2 KB)
该压缩包包含所有VHDL文件、2个测试平台、2个仿真DO文件及Matlab仿真脚本。
文章来源:Digikey