4. 频谱分析
4.4 快速傅里叶变换

4.4.1 Danielson-Lanczos引理
Danielson和Lanczos描述了一种利用DFT的周期性来减少计算需求的方法,即减少计算DFT所需的复乘子的数量。
考虑下面的表达式,它将输入波形分成两个包含偶数和奇数样本的序列。对每个序列分别进行点DFT处理,并对其求和。注意,它仍然对离散值进行运算。

Danielson-Lanczos引理可以推广到8点DFT,如图4.39所示,不需要使用三角函数来计算,而是使用了旋转因子
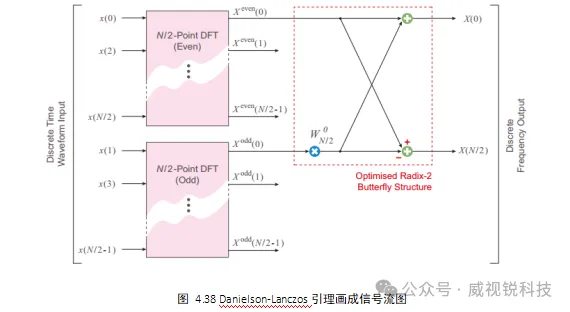
4.4.2 时间抽取
当我们把一个离散的波形分成两个序列,比如奇数和偶数采样时,我们实际上是在对波形进行抽取。Danielson-Lanczos引理可用于在时间上递归抽取,这样我们就可以使用四个2点DFT,而不是上一节中的两个4点DFT。
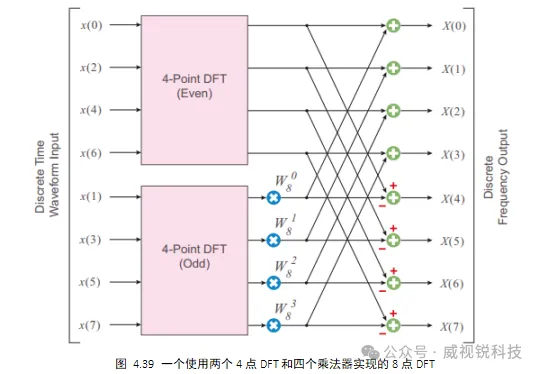
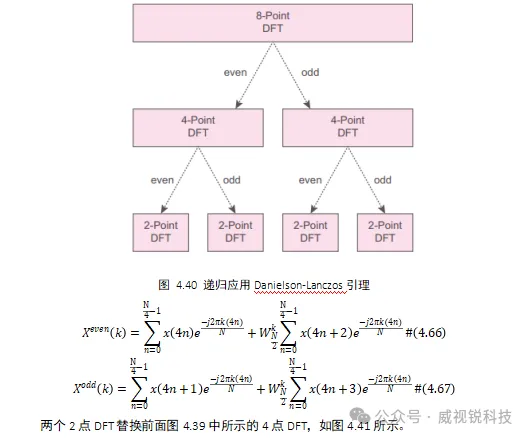
用一个简单的蝴蝶结构来代替2点DFT,8点FFT的最终架构如图4.42所示。

4.4.3 FFT示例
对4.3.2中的示例使用8点FFT的示例图如图4.43所示。
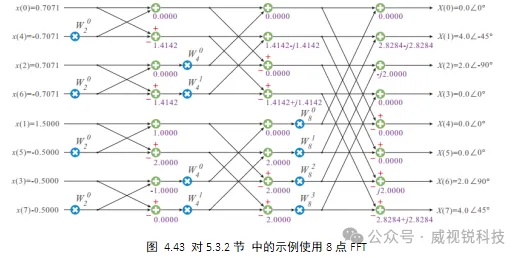
最初,8点DFT需要64个复杂乘法器才能成功操作。上面的设计只需要8个复乘法器。FFT实时抽取方法是一种非常有效的方法,可以在现代计算机系统中实时使用。
4.5 短时傅里叶变换
FFT非常高效且计算复杂度低,使我们能够在现代计算系统上实现实时性能。可以在一段时间内连续执行FFT操作,可以将一个离散的波形分成大小相等的小段,并使用FFT来获得每个段的频率表示。这个过程被称为短时傅里叶变换(STFT)。图4.44给出了一个简单的例子。
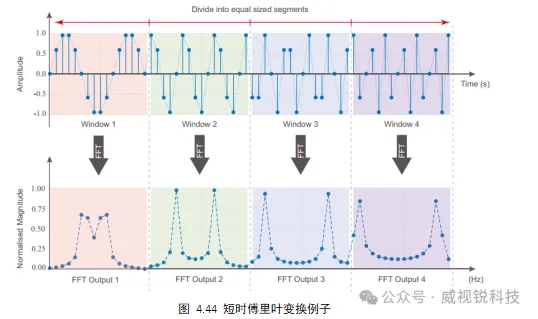
STFT可用于探索离散波形的频谱如何随时间变化。例如,我们可以绘制每个FFT输出作为时间的函数,这被称为频谱图或瀑布图。
4.5.1 Chirp信号的STFT
Chirp信号是一种频率随时间增加或减少的波形,如图4.45所示。

将该Chirp信号分为8个大小相等的片段,并对每个片段应用Hamming窗,再用256点FFT来获得每个片段的频率表示。绘制FFT输出频率随时间的变化图,可以看出频率响应的增加,如图4.46中的二维和三维图所示。
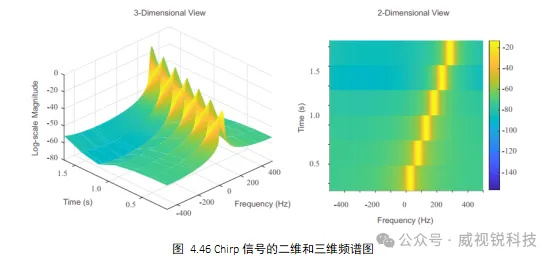
4.5.2 时频分辨率

文章来源:威视锐科技