2. 第二章——信号与系统-2
2.6 软件定义无线电的数字信号处理技术
数字信号处理(DSP)始终处于数学复杂性、计算性能和日益增长的移动性前沿,影响着通信、医学成像、雷达、娱乐乃至科学探索等领域。然而,所有这些领域均依赖于将模拟信息转换为数字表示,并通过某些机制处理这些数据的理念。为此,工程师和科学家依赖包括C语言和Verilog在内的通用工具与语言,这些工具和语言能够以高效且程序化的方式操作数字信息。无论使用何种语言,许多重要的数字信号处理软件问题均与硬件密切相关,例如截断误差、位模式以及处理器的计算速度与效率[14]。 目前,我们将主要忽略这些问题,着重讨论信号处理的算法问题,并介绍常用算法。
2.6.1 离散卷积
卷积是一种将两个信号组合成第三个信号的数学工具,是所有数字信号处理(DSP)的基础。利用冲激分解策略,系统通过称为冲激响应的信号进行描述。卷积的重要性在于它关联了三个关键的信号:输入信号、输出信号和冲激响应。
图2.36展示了卷积在应用于线性系统时的符号表示。一个离散采样的输入信号x[n]进入具有冲激响应的线性系统。
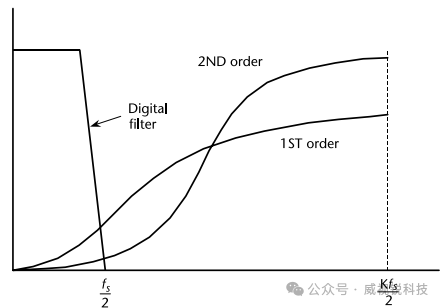
图2.34Σ- 调制器对量化噪声的调节作用
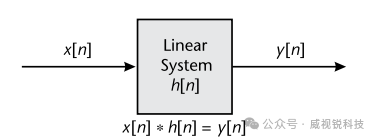
图2.36卷积在数字信号处理中的应用。线性系统的输出信号等于输入信号与系统冲激响应的卷积。
冲激响应h[n]产生输出信号y[n]。 用文字表述,输入信号与冲激响应的卷积等于输出信号。如式(2.41)所示,卷积由∗运算符表示。遗憾的是,大多数编程语言如MATLAB使用星号表示乘法,而通过像MATLAB的conv函数这样特殊函数来表示卷积。计算机程序中的星号表示乘法,而此处的星号表示卷积。
卷积的数学本质由多个乘法与加法运算组成。如果x[n]是一个长度为N的信号,样本索引从0到N−1,且h[n]是一个长度为M的信号,样本索引从0到M −1,则两信号的卷积 y[n] = x[n] ∗ h[n]是一个长度为N+M−1的信号,样本索引从0到N+M−2,其表达式为
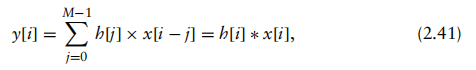
该方程称为卷积和。它允许输出信号中的每个采样点独立于其他采样点进行计算。索引i决定了当前正在计算的输出信号的具体采样位置。此处的n不应与式子y[n]=x[n] ∗h[n]中的n混淆,后者仅作为变量占位符,用于指示数组的索引。MATLAB中两个向量卷积和的实现示例如代码2.16所示。
在信号处理中,卷积可以从两个不同的角度来理解。第一种角度是从输入信号的视角来看卷积,这涉及分析输入信号中的每个采样点如何影响输出信号的多个点。第二种角度是从输出信号的视角来看卷积,考察输出信号中的每个采样点如何从输入信号的多个点接收信息。请注意,这两种视角是对同一数学运算的不同思考方式。
第一种视角十分重要,因为它提供了对卷积在信号处理中作用的概念性理解。第二种视角则描述了卷积的数学本质。这体现了信号处理领域最具挑战性的任务之一,即使你的概念理解与用于表达这些思想的复杂数学语言相契合。
图2.37展示了卷积在低通和高通滤波中的应用,相关内容将在第2.6.4节中详细介绍。示例输入信号是两个分量的和:三个周期的正弦波(代表高频),

图2.37(a)低通滤波和(b)高通滤波的卷积示例。本例中,输入信号由几周期正弦波和一个缓慢上升的斜坡组成。通过使用恰当选择的冲激响应对这两部分信号进行分离。
加上缓慢上升的斜坡信号(由低频组成)。 (a)中,低通滤波器的冲激响应呈平滑拱形,仅允许缓慢变化的斜坡波形传递至输出。类似地,高通滤波器 (b) 仅允许变化较快的正弦曲线通过。
2.6.2 相关
互相关和自相关是软件定义无线电中的两个重要概念。互相关用于衡量两序列的相似程度,其函数关系依赖于其中一序列相对于另一序列的位移。
相关的概念通过示例可以得到最佳说明。图2.38显示了雷达系统的关键组成部分。一个专门设计的天线在选定方向发射一段短时无线电波能量。如果传播波遇到某个物体,如本例中的直升机,部分能量会被反射回位于发射机附近的无线电接收机。发射脉冲具有我们预先选定的特定形状,例如本例中所示的三角形。接收信号由两部分组成:(1) 被偏移和缩放的发射脉冲版本;(2) 由干扰无线电波、电子设备中的热噪声等引起的随机噪声。由于无线信号以已知速度—光速—传播,发射信号与接收信号之间的偏移。
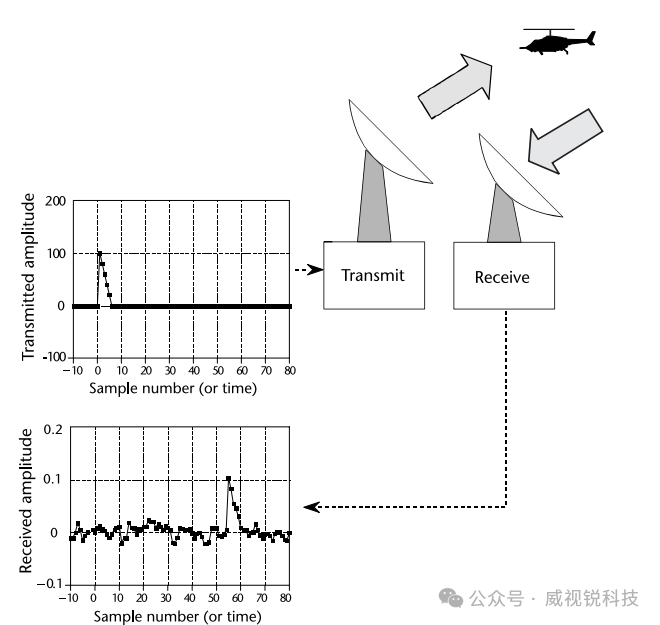
图2.38雷达系统的关键组成部分。与其他回声定位系统类似,雷达发射被检测物体反射的短脉冲能量。因此,接收波形是发射波形的偏移版本,并叠加随机噪声。在噪声信号中检测已知波形是回声定位的基础问题。该问题的解决方案是相关。
脉冲的偏移直接反映了已知形状信号与被检测物体之间的距离。挑战在于确定信号在另一个信号中出现的最佳方式。相关是解决此问题的关键方法。
相关是一种数学运算,与卷积极为相似。与卷积相同,相关运算利用两个信号产生第三个信号。该第三个信号称为两个输入信号的互相关。若一个信号与自身进行相关运算,所得信号则称为自相关。互相关信号中每个采样点的振幅,表征了接收信号在该位置与目标信号的相似程度。这意味着互相关信号中每当存在一个目标信号,便会出现一个峰值。换言之,当目标信号与接收信号中相同的特征对齐时,互相关值达到最大。
相关运算是随机噪声中检测已知波形的最优技术之一。即,利用相关运算所得的峰值相较于任何其他线性系统,均更显著超过噪声水平。(严格而言,该方法仅对随机白噪声具有最优性。)利用相关运算检测已知波形常被称为匹配滤波。更多内容详见第4.7.1节。
对于离散函数f和g,互相关定义为

其中h∗表示h的共轭。函数f(t)与g(t)的互相关等价于f*(−t)与g(t)的卷积,即
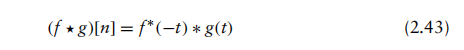
切勿被卷积与相关在数学形式上的相似性所迷惑;二者代表截然不同的信号处理概念。卷积描述系统的输入信号、输出信号与冲激响应之间的关系。
相关是一种用于在噪声背景中检测已知波形的方法。这种类似的数学关系是一种方便的巧合,便于实现算法优化。
2.6.3 Z变换
在第2.1.1节中,我们介绍了傅里叶变换,该变换处理连续时间信号的频域特性。鉴于本节聚焦于数字滤波器设计,涉及离散时间信号,故需引入一种新的变换,即Z变换。
离散时间信号x[n]的Z变换定义为下述幂级数:
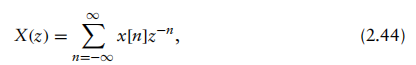
其中z为复变量[1]。
Z变换用于分析离散时间系统。其连续时间对应变换为拉普拉斯变换,定义如下:
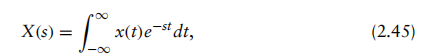
式中, t是以秒为单位的时域时间变量, s=σ +jω是一个复变量。当沿jω轴(即sigma =0)评估时,拉普拉斯变换退化为式(2.2) 中定义的傅里叶变换。因此,拉普拉斯变换将傅里叶变换从实线(频率轴 jω)推广至整个复平面。
根据第2.2.2节,我们知道,若连续时间信号x(t)被均匀采样,其采样信号 xs(t)可表示为
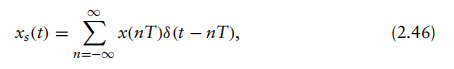
其中T为采样间隔。若对两边取拉普拉斯变换,将得到
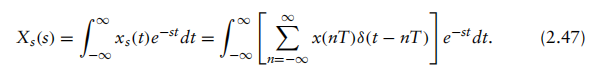
由于积分和求和均为线性算子,我们可以交换它们的顺序。然后,基于德尔塔函数的采样特性,我们可以进一步得到
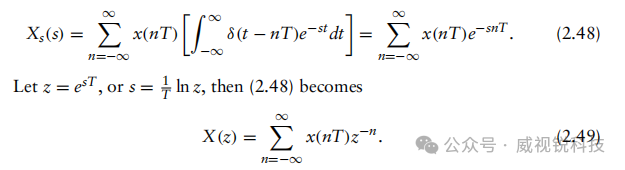
由于T是采样间隔,x(,nT,)=x[n]。上述方程可以进一步写为
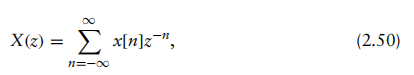
这正是式(2.44)中Z变换的定义。因此,Z变换与拉普拉斯变换之间可以通过以下关系建立联系。
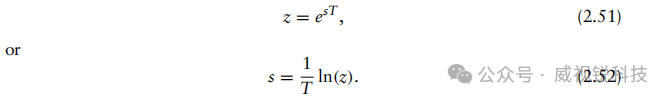
根据式 (2.44),我们知道Z变换是一系列z^{-1}的级数。实际上,除非该级数收敛,否则Z变换无意义。给定一个有限振幅序列x[n],使其Z变换收敛的所有z值的集合称为收敛域(ROC)。 根据级数理论,这些z值必须满足

常用的Z变换对及其收敛域列于表2.4中。
在线性时不变系统分析中,其系统冲激响应的Z变换可表示为两个多项式的比值:
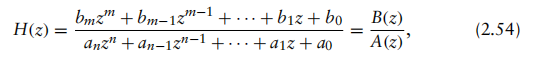
其中A(z)=0的根称为系统的极点(poles),B(z)=0的根称为系统的零点(zeros)。系统可能具有多个极点和零点。若对分子B(z)和分母A(z)进行因式分解,则式(2.54)可表示为:
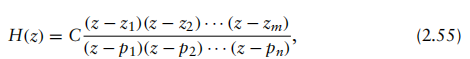
其中C为常数, {pk}为所有极点, {zk}为所有零点。这将帮助我们绘制H(z)的极点零点图。
假设我们有一个线性时不变系统,其系统冲激响应定义为
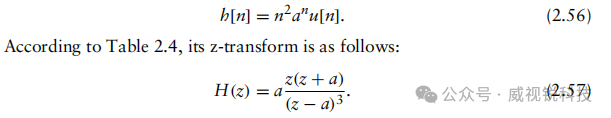
比较(2.57)与(2.55),可知该系统有两个零点,z1=0和z2=−a,以及三个极点, p1=p2=p3=a。 因此,其极点零点图如图2.39所示。
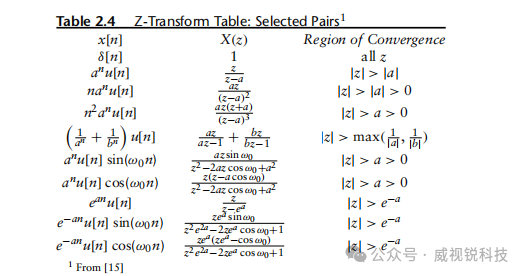
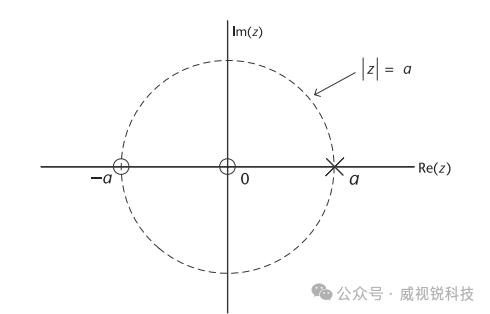
图2.39 由(2.57)定义的系统的极点零点图。极点以叉号表示,零点以圆圈表示。该系统的收敛区域为圆 z= |a|之外的区域。
Z变换具有若干性质,在研究Z变换域中的信号与系统时十分有用。由于这些性质与第2.1.1节中介绍的傅里叶变换性质极为相似,故在表2.5中列出,且不再赘述。
2.6.4 数字滤波
在进行信号处理时,我们通常需要去除噪声并提取有用信号。此过程称为滤波,所使用的设备称为滤波器,其根据加于输入端信号的某些属性,决定通过的成分。典型的滤波器是一种频率选择电路。若噪声与有用信号的频率分布不同,且同时存在于滤波器输入端,则应用该电路可使噪声衰减甚至消除,而保留有用信号。
滤波器可从不同角度进行分类。例如,根据频率响应,滤波器可分为低通、高通、带通及带阻。根据所处理的信号类型,滤波器可分为模拟滤波器或数字滤波器[1]。 具体而言,模拟滤波器处理连续时间信号,而数字滤波器处理离散时间信号。本节将重点介绍数字滤波器。这些类型滤波器的理想幅度响应特性如图2.40所示。根据图2.40,理想滤波器的幅度响应特性可概括如下:在通带内幅度恒定,而在阻带内幅度降为零。然而,实际中无法实现此类理想滤波器,因此实用滤波器实际上是对理想滤波器的最优近似。
为了实现数字滤波,数字系统的输入和输出均须为离散时间序列。若输入序列为x[n],滤波器的冲激响应为h[n],则输出序列y[n]为

![1767577612629353.png 图2.40频率范围[0, 2π]上四种滤波器的理想幅度响应特性.png](https://static.eetrend.com/files/ueditor/108/upload/image/20260105/1767577612629353.png)
图2.40频率范围[0, 2π]上四种滤波器的理想幅度响应特性。(a) 低通滤波器,(b) 高通滤波器,(c) 带通滤波器,其中(ωc1,ωc2)为通带,(d) 带阻滤波器,其中(ωc1,ωc2)为阻带。
根据表2.5中的时间卷积性质,在频域上,式(2.58)等价于

其中X(z)和Y(z)分别是输入序列x[n]和输出序列y[n]的Z变换,H(z)是序列h[n]的Z变换。
由于理想砖墙滤波器在实际中不可实现,我们将注意力限制在由差分方程[1]描述的线性时不变系统类别上:
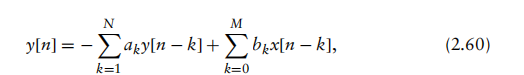
其中y[n]为当前滤波器输出,y[n−k]为先前滤波器输出,x[n−k]为当前或先前滤波器输入。该系统的频率响应如下:

其中 {ak}为滤波器的反馈系数,对应滤波器的极点,{bk}为滤波器的前馈系数,对应滤波器的零点,N为滤波器的阶数。
基本数字滤波器设计问题是通过合理选择系数 {ak}和 {bk},用具有频率响应(2.61)的系统逼近任意理想频率响应特性[1]。
数字滤波器基本有两种类型:有限冲激响应(FIR)滤波器和无限冲激响应(IIR)滤波器。当系统受到单位抽样δ[n]激励时,系统的冲激响应 h[n]可能持续有限时间,如图2.41(a)所示;也可能自输入施加之前便一直存在且持续无限时间,如图2.41(b)所示。前者称为有限冲激响应系统,后者称为无限冲激响应系统。长度为M的FIR滤波器,其输入为 x[n],输出为y[n],可由差分方程[1]描述:
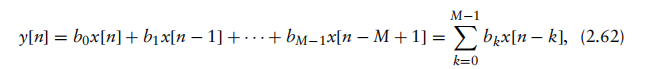
其中滤波器无反馈系数{ak},故H(z)仅含零点。
IIR滤波器在式(2.60)中定义,含一个或多个非零反馈系数{ak}。 因此,滤波器一旦受单位脉冲激励,输出将持续存在。
2.6.4.1 案例研究:级联积分-梳状滤波器
级联积分-梳状滤波器(CIC滤波器)在软件定义无线电硬件中具有重要作用。该滤波器由Eugene B. Hogenauer发明,属于用于多速率信号处理的一类FIR滤波器。CIC滤波器广泛应用于插值与降采样。然而,与大多数FIR滤波器不同,其体系结构中内置了一个降采样器或插值器[16]。
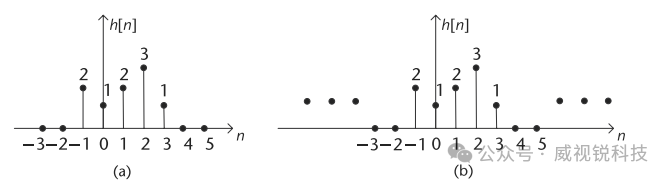
图2.41FIR滤波器和IIR滤波器的冲激响应。(a) FIR滤波器的冲激响应,(b) IIR滤波器的冲激响应。
CIC滤波器由一个或多个积分器和梳状滤波器对组成。在降采样CIC中,输入信号依次通过一个或多个级联积分器,然后经过降采样器,之后通过数量等同于积分器数量的一个或多个梳状滤波器段。插值CIC则是上述结构的逆过程,用上采样器代替降采样器,如图2.42所示。
为说明梳状滤波器的一种简单形式,考虑由差分方程描述的移动平均FIR滤波器:
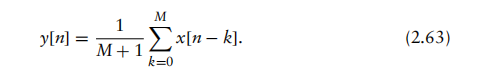
该FIR滤波器的系统函数为
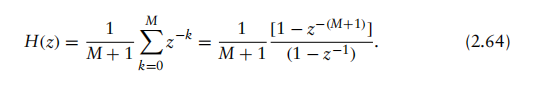
假设用zL替代z,其中L为正整数;则得到的梳状滤波器系统函数为:
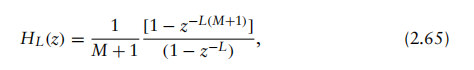
其中L为降采样或插值比率,M为每级样本数,通常取1或2。
该滤波器在单位圆上具有零点,位于

对所有整数值的k均适用,除非k=0, L, 2L, ..., ML,如图2.43所示。常见的CIC滤波器形式通常由多个级联阶段组成,复合CIC滤波器的系统函数为
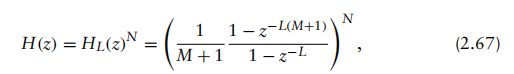
其中N为复合滤波器中的级数。
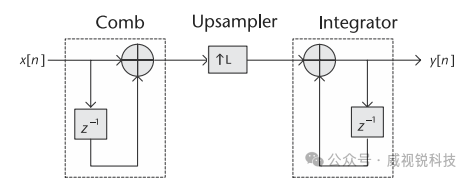
图2.42插值级联积分器-梳状滤波器结构[17],其输入信号为x[n],输出信号为y[n]。 该滤波器由一对梳状滤波器与积分器滤波器组成,配合插值比率为L的上采样器。
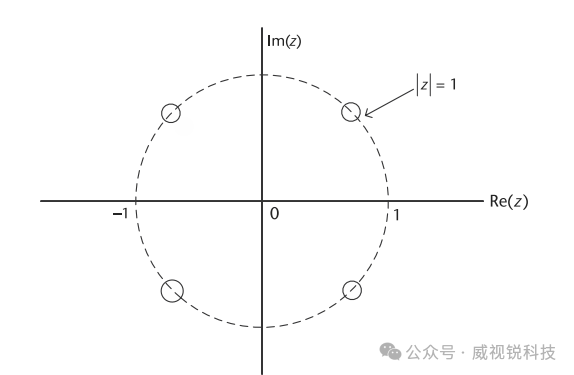
图2.43 式(2.65)中定义的CIC滤波器的零点分布,所有零点均位于单位圆上。
CIC滤波器的特性包括线性相位响应,并且仅采用延迟、加法和减法运算。换言之,该滤波器不涉及乘法运算,因此适合硬件实现。
2.6.4.2 案例研究:FIR半带滤波器
FIR半带滤波器在多率信号处理中广泛应用,尤其是在插值和抽取操作中。半带滤波器采用多相结构可高效实现,因为其约一半的系数为零。半带滤波器具有两个重要特性:通带波纹与阻带波纹相同,且通带边缘频率与阻带边缘频率相对于半带频率f4s对称分布。
例如,Pluto软件定义无线电在接收和发射链路中配备多个可编程半带滤波器。RX HB3/DEC3提供两种不同的固定系数降采样滤波器,可选择的降采样因子为2、3或1(旁路)。 滤波器的输入信号(ADC 输出)为24,即 16个采样值。
当使用RX HB3滤波器时,降采样因子设为 2,采用以下系数:[1, 4, 6, 4, 1]。 注意,RX HB3滤波器的满量程范围为16(24)。 当使用RX DEC3滤波器时,降采样因子设为 3。 其系数如下:[55, 83, 0, -393, -580, 0, 1914, 4041, 5120, 4041, 1914, 0, -580, -393, 0, 83, 55]。RX DEC3滤波器的满量程范围为16384(214)。
文章来源:威视锐科技