版权声明:本文为CSDN博主「jerwey」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/jerwey/article/details/107541077
Vivado HLS工具支持C/C ++浮点和双精度数据类型,它们基于IEEE-754标准定义的单、双精度二进制浮点格式。浮点数值格式由于精度有限不能表示每个实数。
计算不匹配的来源包括
(subnormals有时用于表示比普通浮点格式所能表示的数字小的数字。例如,在单精度格式中,最小的标准浮点值是2-126。但是,当支持subnormals时,尾数位用于表示具有固定指数值2-127的定点数。)
正规数、次正规数 见 https://www.cnblogs.com/HDK2016/p/10506083.html
(把常量表达式的值求出来作为常量嵌在最终生成的代码中,这种优化叫做常量折叠(constant folding))
(常数传播(constant propagation)都是编译器最佳化技术,被使用于现代的编译器中。)
使用Vivado HLS工具进行浮点设计的基础知识
尽管可以使用CORE Generator工具为自定义精度浮点类型生成这些内核,但是Vivado HLS工具仅生成IEEE-754标准描述的内核的单精度和双精度版本。
基于浮点运算符内核的软件与硬件生成的结果可能(微小)差异的来源是,这些内核通过“冲洗为零”来处理次标准输入(subnormal inputs),也就是说,遇到这种情况时将它们替换为0.0。
在基于ANSI / ISO-C的项目中使用
要在基于ANSI/ISO-C的项目中使用受支持的标准数学库函数,math.h头文件应该包含在所有调用它们的源文件中。基函数用于操作(并返回)双精度值,例如,double sqrt(double)。
大多数函数的单精度版本都在函数名后面附加了一个“f”,例如,float sqrtf(float)、float sinf(float)和float ceilf(float)。记住这一点很重要,因为如果不这样做,即使参数和返回变量是单精度的,也会实现更大的(在FPGA资源中)双精度版本,而且会使用额外的资源并增加计算的延迟。
在ANSI/ISO-C中工作时的另一个考虑是,当将代码作为软件编译和运行时(包括RTL co-simulation期间的C测试台端),使用的算法与在HLS生成的RTL中实现的算法不同。在软件中,调用GCC libc函数,在硬件端使用Vivado HLS工具math library代码。这可能导致两者之间的位级不匹配(bit-level mismatches ),当两个结果可能非常接近实际答案(在分析意义上)时.
Example 3: Unintended Use of Double-Precision Math Function:
// Unintended consequences?
#include
float top_level(float inval)
{
return log(inval); // double-precision natural logarithm
}
这个示例生成了一个RTL实现,它将输入转换为双精度格式,以双精度计算自然对数,然后将结果转换为单精度输出
Example 4: Explicit Use of Single-Precision Math Function:
// Be sure to use the right version of math functions...
#include
float top_level(float inval)
{
return logf(inval); // single-precision natural logarithm
}
return logf(inval); // single-precision natural logarithm 因为调用了对数函数的单精度版本,所以该版本在RTL中实现,不需要进行输入/输出格式转换
Using in C++ Projects
使用C ++设计时,获得对标准数学库的支持的最直接方法是在所有调用其函数的源文件中包括
这个头文件提供了重载的基(双精度)函数的版本,以接受参数并在std名称空间中返回单精度(浮点)值。
对于要使用的单精度版本,必须通过作用域解析操作符(::)或通过使用using指令导入整个名称空间,将std名称空间包含在范围内。
C++ 的基函数对于单精度浮点、双精度浮点使用重载的方式。在使用单精度时方法如下
std:: 或 using namespace std
Example 5: Explicit Scope Resolution:
// Using explicit scope resolution
#include
float top_level(float inval)
{
return std::log(inval); // single-precision natural logarithm
}
Example 6: Exposing Contents of a Namespace to File Scope:
// import std:: namespace
#include
using namespace std;
float top_level(float inval)
{
return log(inval); // single-precision natural logarithm
}
当在由Vivado HLS工具合成的代码中使用cmath的函数时,软件运行的代码与RTL实现之间的结果可能会不同,因为使用了不同的近似算法。
因此,可以访问用于合成RTL的算法,以用于C ++建模。?
当验证HLS的C++代码,以及使用C++的测试平台对RTL进行co-simulating时,建议HLS源码调用相同的数学库,而测试代码使用 C++标准库生成参考值。这为开发期间的HLS模型和数学库提供了额外的验证。
为了遵循这种方法,Vivado HLS头文件
hls_math头文件中的函数是HLS::名称空间的一部分。
对于要为软件建模/验证而编译的HLS版本,请对每个函数调用使用hls ::作用域解析。
NOTE:在使用c++标准数学库调用时,不建议导入hls:: namespace(通过’using namespace hls’),因为这可能导致在hls期间出现编译错误。
示例7a说明了这种用法
测试程序7a使用标准的c++数学库
Example 7a: Test Program Uses Standard C++ Math Library:
// Contents of main.cpp - The C++ test bench
#include
#include
using namespace std;
extern float hw_cos_top(float);
int main(void)
{
int mismatches = 0;
for (int i = 0; i < 64; i++) {
float test_val = float(i) * M_PI / 64.0f;
float sw_result = cos(test_val); //float std::cos(float)
float hw_result = hw_cos_top(test_val);
if (sw_result != hw_result) {
mismatches++;
cout << "!!! Mismatch on iteration #" << i;
cout << " -- Expected: " << sw_result;
cout << "\t Got: " << hw_result;
cout << "\t Delta: " << hw_result - sw_result << endl;
}
}
return mismatches;
}
Example 7b: The HLS Design Code Uses the hls_math Library
// Contents of hw_cos.cpp
#include
float hw_cos_top(float x)
{
return hls::cos(x); // hls::cos for both C++ model and RTL co-sim
}
将此代码编译并作为软件运行后(例如,Vivado HLS GUI中的“运行C / C ++项目”),hw_cos_top()返回的结果与HLS生成的RTL产生的值相同,并且程序会测试与软件参考模型的不匹配情况,即std :: cos()。
如果在hw_cos.cpp中包含头文件
其他事项
不要假设Vivado HLS工具所做的优化对于人眼而言似乎是显而易见的且微不足道的。 与大多数C / C ++软件编译器一样,在HLS期间可能无法优化涉及浮点数(数字常量)的表达式。 考虑以下示例代码。?
同样运算目的,不同表达。产生RTL以及结果精度都不一样。
Example 8: Algebraically idEntical; Very Different HLS Implementations:
// 3 different results
void top(float *r0, float *r1, float *r2, float inval)
{
*r0 = 0.1 * inval; // double-precision multiplier & conversions 不是精确的
*r1 = 0.1f * inval; // single-precision multiplier 不是精确的
*r2 = inval / 10.0f; // single-precision divider 可能是精确的
}
r0 r1 r2 的运算目的都是乘0.1,不仅RTL电路不一样,结果也不一样。分析如下:
r0:根据C/C++的规则,文字值0.1表示无法精确表示的双精度数,因此,实例化了双精度(double)乘法器core,以及将inval转换为double的core,并将结果乘积变回float(*r0的类型是float)的core。
r1:当需要单精度(浮点)常数时,必须将f附加到文字值,例如0.1f。因此,上面r1的值是(不精确的)浮点数表示0.100和inval之间的单精度乘法的结果。
r2:最后,r2 由单精度除法core产生, inval为分子,10.0f为分母。实数10(1010)是用二进制浮点格式精确表示的,因此(取决于inval的值),计算r2可能是精确的,而r0和r1可能都不是精确的。
Note:因为浮点运算的发生顺序可能会影响结果(例如,由于在不同时间舍入),所以表达式中涉及的多个浮点文字可能不会合并在一起
Example 9: Order of Operations Can Impact Constant Folding:
操作数顺序影响常数合并
// very different implementations
void top(float *r0, float *r1, float inval)
{
*r0 = 0.1f * 10.0f * inval; // *r0 = inval; constants eliminated
*r1 = 0.1f * inval * 10.0f; // two double-precision multiplies
}
在上面的示例中,由于分配给r0的表达式的求值顺序,编译器会将整个表达式识别为恒等式,因此不会生成任何硬件。但是,同样的情况不适用于r1;做了两次乘法。
Example 10: Avoid Floating Point Literals in Integer Expressions:
void top(int *r0, int *r1, int inval)
{
*r0 = 0.5 * inval; //
*r1 = inval / 2; //移位实现高效
}
对于本例,HLS实现r0的逻辑,方法是将inval转换为双精度格式,将其乘以0.5(一个双精度数值),然后将其转换回整数。
另一方面,HLS将2的整数幂的乘法和除法分别优化为左移和右移操作,这在硬件中被实现为简单的线选择(根据操作数的方向和类型使用零填充或符号扩展)。因此,在实现相同的算术结果时,为r1而创建的逻辑要高效得多。
并行性、并发性和资源共享
Resource Sharing
Vivado HLS工具会尽可能高效地利用浮点资源。当数据依赖和约束允许时,浮点运算符核通常在源操作的多个调用之间共享。为了说明这个概念,下面的示例将四个浮点值相加。
Example 11: Multiple Operations Use Single Core:
// How many adder cores?
void top (float *r, float a, float b, float c, float d)
{
*r = a + b + c + d;
}
//使用2个DSP48E
当数据带宽允许时,可能需要在给定的时间内并发地执行许多操作来完成更多的工作,否则这些操作将按顺序安排。在下面的示例中,结果数组中的值 是通过在流水线循环中对两个源数组的元素 进行求和生成的。
Vivado HLS将顶层数组参数映射到存储器接口,因此,每个周期的访问次数是有限的,例如,双端口RAM每个周期访问两次,FIFO每个周期访问一次,等等。
Example 12: Independent Sums:
// Independent sums, but I/O only allows throughput of one result per cycle
void top (float r0[32], float a[32], float b[32])
{
#pragma HLS interface ap_fifo port=a,b,r0
for (int i = 0; i < 32; i++) {
#pragma HLS pipeline
r0[i] = a[i] + b[i];
}
}
默认情况下,Vivado HLS工具将该循环安排为迭代32次并实现单个加法器核。 如果输入数据是连续可用的,并且输出FIFO永远不会满,则生成的RTL块需要32个周期,外加一些刷新加法器的流水线。
Concurrency
扩展前面的示例,使用Vivado HLS工具的array reshape指令,通过将接口的宽度加倍来增加I / O带宽。 为了提高处理速度,将loop部分展开两倍,以匹配带宽的增加。
Example 13: Independent Sums:
// Independent sums, with increased I/O bandwidth -> high throughput and
area
void top (float r0[32], float a[32], float b[32])
{
#pragma HLS interface ap_fifo port=a,b,r0
#pragma HLS array_reshape cyclic factor=2 variable=a,b,r0
for (int i = 0; i < 32; i++) {
#pragma HLS pipeline
#pragma HLS unroll factor=2
r0[i] = a[i] + b[i];
}
}
通过添加指令,Vivado HLS工具合成的RTL有两个adder管道。
接下来,将给出Vivado HLS工具如何通过浮点运算处理反馈/重复发生的详细示例,然后讨论如何在这种情况下提高性能。
Dependency
Example 14: Dependency through an Operation:
// Floating point accumulator
float top(float x[32])
{
#pragma HLS interface ap_fifo port=x
float acc = 0;
for (int i = 0; i < 32; i++) {
#pragma HLS pipeline
acc += x[i];
}
return acc;
}
由于在递归式中实现累加,而浮点加的延迟通常大于一个周期,所以这条管道不能达到每个周期的一个累加的吞吐量。
如果浮点adder有4个latency的延迟,那么管道启动区间也是四个周期,因为依赖项要求每个累积在另一个可以开始之前完成。因此,可以实现的最好的吞吐量是每4个周期的累积。累积循环迭代32次,每次行程进行四个周期,总共达到128个周期,再加上一些来刷新管道。
更高性能的替代方法可能是将四个部分累加交织到同一加法器内核上,每个累加器每四个周期完成一次,从而减少了完成32个加法运算的时间。但是,Vivado HLS工具无法从上面提供的代码中推断出这种优化,因为它需要更改累加操作的顺序。 如果每个部分累加都将x []的第四个元素作为输入,则各个和的顺序将发生变化,这可能会导致不同的结果。
可以通过对源代码进行少量修改来解决此限制,以使设计者的意图更加明确。 以下示例代码引入了一个数组acc_part [4],用于存储部分和,该部分和随后被求和,并且主累积循环被部分展开。
Example 15: Explicit Reordering of Operations for Better Performance:
// Floating point accumulator
float top(float x[32])
{
#pragma HLS interface ap_fifo port=x
float acc_part[4] = {0.0f, 0.0f, 0.0f, 0.0f};
for (int i = 0; i < 32; i += 4) { // Manually unroll by 4
for (int j = 0; j < 4; j++) { // Partial accumulations
#pragma HLS pipeline
acc_part[j] += x[i + j];
}
for (int i = 1; i < 4; i++) { // Final accumulation
#pragma HLS unroll
acc_part[0] += acc_part[i];
}
return acc_part[0];
}
}
使用这个代码结构,Vivado HLS工具识别到它可以将四个部分累积安排在交替循环的一个adder核心上,这是更有效地使用资源(参见图3)。后续的最终积累可能还使用相同的adder核心,这取决于其他因素。
现在,主要的累积循环在8次迭代(32/4)中完成,每一次进行四个周期来产生4个部分累积。
在FPGA资源小增加的情况下,同样数量的工作完成的时间更短。最后的累积循环,同时使用相同的adder核心,增加额外的循环,但是这个数字是固定的和小的相对于节省的主要积累循环,特别是当数据集大的时候。最后的累积步骤可以进一步优化,但相对于性能和区域的回报递减。
当更大的I / O带宽可用时,可以指定更大的不滚动因素,以带来更多的算术核心。如果在前面的例子中,每一个时钟周期中有两个x[]元素,则不滚动因子可以增加到8,在这种情况下,将实现两个adder内核,每个周期进行8次部分累积。精确的操作员延迟可能受到目标设备选择和用户时间限制的影响。一般来说,需要运行HLS,并对一个简单的基本情况进行一些性能分析。以表14为例,确定最优的未滚动量。
控制实现的资源
Xilinx LogiCORE IP浮点运算符内核允许控制某些支持的操作对DSP48的利用。 例如,乘法器内核具有四个变体,可以替代逻辑(LUT)资源以使用DSP48。
通常,Vivado HLS工具会根据性能限制自动确定要使用的内核类型。 Vivado HLS工具的RESOURCE指令可用于覆盖自动选择并指定给定操作实例使用哪种类型的浮点运算符核。
例如,对于示例14中所示的代码,加法器通常使用Kintex -7 FPGA上的两个DSP48E1资源,使用“完全使用”内核来实现,如综合报告的“组件”部分所示(请参见图4)。
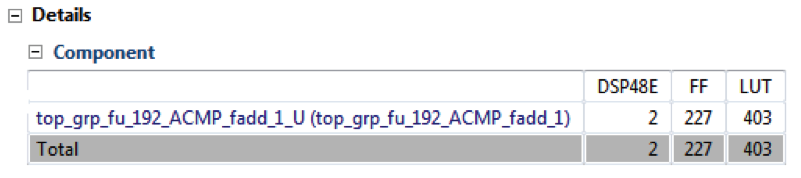
在下面的示例代码中,强制将加法操作映射到FAddSub_nodsp核心。
// Floating point accumulator
float top(float x[32])
{
#pragma HLS interface ap_fifo port=x
float acc = 0;
for (int i = 0; i < 32; i++) {
#pragma HLS pipeline
#pragma HLS resource variable=acc core=FAddSub_nodsp
acc += x[i];
}
return acc;
}
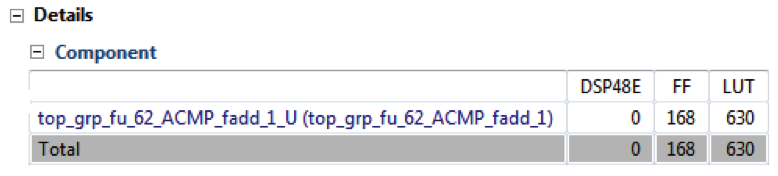
请参见UG902,了解资源指令使用的详细信息和可用核列表。
验证
通过不同的方法完成的相同浮点计算,其结果之间存在位级(或更大)不匹配的原因有很多。例如,不同的近似算法,对操作进行重新排序以导致舍入差异以及处理非正规subnormal(浮点运算核将其刷新为零)。 一般来说,两个浮点值对比的结果(特别是相等值)可能会引起误解。被比较的两个值可能是最后一个“单位”不同(unit in the last place,ULP;其二进制格式的最低有效位),它可以表示一个非常小的相对错误,但是’ = = ‘运算符返回false。例如,在使用单精度浮点格式时,如果两个操作数都是非零(and non-subnormal)值,一个ULP的不同表示在0.00001%的量级上的相对错误。因此,优良作法是避免使用’==‘和’!='运算符比较浮点数。相反,建议通过引入可接受的错误阈值来检查值是否“足够接近”。
大多数情况,设置一个可接受的ULP或相对错误水平可以很好地工作,并且比绝对误差(或“ε”)阈值更可取。
但是,当被比较的其中一个值恰好为零(0.0)时,此方法就失效了。 如果被比较的某个值可以取零值(或具有常量),那么应该使用绝对错误阈值。
下面的示例代码提供了一种方法,该方法可用于比较两个浮点数以实现近似相等,并允许用户设置ULP和绝对错误限制。
此功能旨在用于C / C ++“测试台”代码中,以验证对HLS源代码的修改并在RTL co-simulation过程中进行验证。 类似的技术也可以在用于HLS实现的代码中使用。
Example 17: C Code to Test Floating Point Values for Approximate Equivalence:
// Create a union based type for easy access to binary representation
typedef union {
float fval;
unsigned int rawbits;
} float_union_t;
bool approx_eqf(float x, float y, int ulp_err_lim, float abs_err_lim)
{
float_union_t lx, ly;
lx.fval = x;
ly.fval = y;
// ULP based comparison is likely to be meaningless when x or y
// is exactly zero or their signs differ, so test against an
// absolute error threshold this test also handles (-0.0 == +0.0),
// which should return true.
// N.B. that the abs_err_lim must be chosen wisely, based on
// knowledge of calculations/algorithms that lead up to the
// comparison. There is no substitute for proper error analysis
// when accuracy of results matter.
if (((x == 0.0f) ^ (y == 0.0f)) || (__signbit(x) != __signbit(y))) {
#ifndef NDEBUG
if (x != y) { // (-0.0 == +0.0) so warning not printed for that case
printf("\nWARNING: Comparing floating point value against zero ");
printf("or values w/ differing signs. ");
printf("Absolute error limit has been used.\n");
}
#endif
return fabs(x - y) <= fabs(abs_err_lim);
}
// Do ULP base comparison for all other cases
return abs((int)lx.rawbits - (int)ly.rawbits) <= ulp_err_lim;
}
缩减版
但是,当被比较的其中一个值恰好为零(0.0)时,此方法就失效了。 如果被比较的某个值可以取零值(或具有常量),那么应该使用绝对错误阈值。