本文转载自:Linest-5的CSDN博客
注:本文由作者授权转发,如需转载请联系作者本人
为什么使用 FIFO
当我们需要在两个模块之间进行数据的传输,并且两个模块的时钟是不同的,当一定数量数据传输时为了避免数据出现丢失,而且此时写入数据速率大于读出数据速率时,这时候需要将利用 FIFO 做缓冲。
FIFO 的深度大小
FIFO 的深度(大小)应使 FIFO 可以存储所有较慢的模块不读取的数据。 FIFO 仅在数据以突发形式出现时才起作用;不能有连续的数据进出(比如ADC连续采集数据)。如果有连续的数据流,那么所需的 FIFO 应该是无限的。需要知道突发速率、突发大小、频率等来确定适当的FIFO大小。
确定 FIFO 的大小的逻辑是为了找到数据的第几位,这些数据在某段时期没有读出或写入操作已经完成。换句话说,FIFO 的深度等价于还没有被读出的数据量。按照这个逻辑,固定 FIFO 的大小应用在不同的场景中,而不使用任何无法使用的标准公式每个场景。
题型及解答
以下示例描述了不同的可能场景,其中需要异步 FIFO。在以下示例中,我认为模块 A 想要向模块 B 发送一些数据。
f:时钟频率
idle cycles:闲置循环,指的是并不是每个时钟周期都连续,可能中间存在空闲一段时间
burst:一次性发送的数据量

情况1:
fA > fB ,写入和读取都没有空闲周期(idle cycles)。
Writing frequency = fA = 80MHz
Reading Frequency = fB = 50MHz
Burst Length = 一次性要传输的数据量 = 120
读取和写入都没有空闲周期,这意味着突发中的所有数据都将在连续的时钟周期内写入和读取。
解答:
写入一个数据所需的时间 = 1/80MHz = 12.5ns
在一次突发中写入所有数据所需时间 = 12.5ns * 120 = 1500ns
读取一个数据所需的时间 = 1/50MHz = 20ns
每 20 ns,模块 B 将在突发中读取一个数据。
在1500ns内,120个数据可以被写入,则在1500ns内可以被读出的数据量为:
1500ns / 20ns = 75个
因此剩下没有读出的数据需要暂时缓存在 FIFO 当中,则 FIFO 的深度为:
120 - 75 = 45,因此 FIFO 的最小深度为45。
情况2:
fA > fB ,两次连续读取和写入之间有一个 clk 周期延迟。
解答:
这只是为了制造某种混乱。这种情况与前一种情况(情况1)没有什么不同,因为在两次连续读取和写入之间总是会有一个时钟周期延迟。因此该方法与之前的方法相同。
情况3:
fA > fB ,写入和读取都有空闲周期
Writing frequency = fA = 80MHz
Reading Frequency = fB = 50MHz
Burst Length = 一次性要传输的数据量 = 120
两次连续写入之间的空闲周期数 = 1
两次连续读取之间的空闲周期数 = 3
解答:
两次连续写入之间的空闲周期为 1 个时钟周期。这意味着,在写入一个数据后,模块 A 正在等待一个时钟周期,以启动下一次写入。因此可以理解为每两个时钟周期写入一个数据。
两次连续读取之间的空闲周期为 3 个时钟周期。这意味着,在读取一个数据后,模块 B 正在等待 3 个时钟周期,以启动下一次读取。因此可以理解为每四个时钟周期读取一个数据。
写入一个数据所需的时间 = 2 * 1/80MHz = 25ns
在一次突发中写入所有数据所需时间 = 25ns * 120 = 3000ns
读取一个数据所需的时间 = 4 * 1/50MHz = 80ns
每 80 ns,模块 B 将在突发中读取一个数据。
在3000ns内,120个数据可以被写入,则在3000ns内可以被读出的数据量为:
3000ns / 80ns = 37.5个
因此剩下没有读出的数据需要暂时缓存在 FIFO 当中,则 FIFO 的深度为:
120 - 37.5 = 82.5,因此 FIFO 的最小深度为83(直接进1位)。
情况4:
fA > fB ,占空比为 wr_enb 和 rd_enb
Writing frequency = fA = 80MHz
Reading Frequency = fB = 50MHz
Burst Length = 一次性要传输的数据量 = 120
wr_enb(写使能)的占空比 = 50 % = 1/2
wr_enb(写使能)的占空比 = 25 % = 1/4
解答:
这种情况与前一种情况(情况 3)没有什么不同,因为在这种情况下,一个数据项将在 2 个时钟周期内写入,一个数据项将在 4 个时钟周期内读取。
注意:情况 2 和情况 4 的解释是为了让大家明白同样的问题可以用不同的方式提出。
情况5:
fA < fB在写入和读取中都没有空闲周期(即延迟两次连续写入和读取之间是一个时钟周期)
Writing frequency = fA = 30MHz
Reading Frequency = fB = 50MHz
Burst Length = 一次性要传输的数据量 = 120
读取和写入都没有空闲周期,这意味着突发中的所有项目都将在连续的时钟周期内写入和读取
解答:
在这种情况下,深度为 1 的 FIFO 就足够了,因为读比写快,不会有任何数据丢失。
情况6:
fA < fB ,写入和读取都有空闲周期(wr_enb 的占空比并且 rd_enb 也可以在这些类型的问题中给出)。
Writing frequency = fA = 30MHz
Reading Frequency = fB = 50MHz
Burst Length = 一次性要传输的数据量 = 120
两次连续写入之间的空闲周期数 = 1
两次连续读取之间的空闲周期数 = 3
解答:
两次连续写入之间的空闲周期为 1 个时钟周期。这意味着在写入一个数据后,模块 A 正在等待 1 个时钟周期,以启动下一次写入。因此可以理解为每两个时钟周期写入一个数据。
两次连续读取之间的空闲周期为 3 个时钟周期。这意味着在读取一个数据后,模块 B 正在等待 3 个时钟周期,以启动下一次读取。因此可以理解为每四个时钟周期读取一个数据。
写入一个数据所需的时间 = 2 * 1/30MHz = 66.667ns
在一次突发中写入所有数据所需时间 = 66.667ns * 120 = 8000ns
读取一个数据所需的时间 = 4 * 1/50MHz = 80ns
每 80 ns,模块 B 将在突发中读取一个数据。
在8000ns内,120个数据可以被写入,则在8000ns内可以被读出的数据量为:
8000ns / 80ns = 100个
因此剩下没有读出的数据需要暂时缓存在 FIFO 当中,则 FIFO 的深度为:
120 - 100 = 20,因此 FIFO 的最小深度为20。
情况7:
fA = fB ,写入和读取都没有空闲周期(两次连续写入和读取之间的延迟为一个时钟周期)
Writing frequency = fA = 30MHz
Reading Frequency = fB = 30MHz
Burst Length = 一次性要传输的数据量 = 120
读取和写入都没有空闲周期,这意味着突发中的所有数据都将在连续的时钟周期内写入和读取
解答:
如果 clkA和 clkB之间没有相位差,则不需要 FIFO。
如果clkA和 clkB之间有相位差,则一个深度为 1 的 FIFO 即可解决。
情况8:
fA = fB ,写入和读取都有空闲周期(wr_enb 和 rd_enb 的占空比也可以在这类问题中给出)
Writing frequency = fA = 50MHz
Reading Frequency = fB = 50MHz
Burst Length = 一次性要传输的数据量 = 120
两次连续写入之间的空闲周期数 = 1
两次连续读取之间的空闲周期数 = 3
解答:
两次连续写入之间的空闲周期为 1 个时钟周期。这意味着,在写入一个数据后,模块 A 正在等待 1 个时钟周期,以启动下一次写入。因此可以理解为每 2 个时钟周期,写入一个数据。
两次连续读取之间的空闲周期为 3 个时钟周期。这意味着,在读取一个数据后,模块 B 正在等待 3 个时钟周期,以启动下一次读取。因此可以理解为每 4 个时钟周期,读取一个数据。
写入一个数据所需的时间 = 2 * 1/50MHz = 40ns
在一次突发中写入所有数据所需时间 = 40ns * 120 = 4800ns
读取一个数据所需的时间 = 4 * 1/50MHz = 80ns
每 80 ns,模块 B 将在突发中读取一个数据。
在4800ns内,120个数据可以被写入,则在4800ns内可以被读出的数据量为:
4800ns / 80ns = 60个
因此剩下没有读出的数据需要暂时缓存在 FIFO 当中,则 FIFO 的深度为:
120 - 60 = 60,因此 FIFO 的最小深度为60。
情况9:
如果数据速率如下给出。
写入数据 = 80 数据/100 时钟(20 个数据的随机化)
输出数据= 8 数据/10 时钟。
突发大小 = 160
解答:
给定的规格表明写入频率等于读取频率。但是,读取和写入都可以在任何随机时刻发生,具有“80 个数据项的写入将在 100 个周期内完成”和“8 个数据项的读取将在 10 个周期内完成”的约束。
这样就要分析写入数据在 100 个时钟内是如何排列的,以及读取数据在 10 个时钟周期内是如何排列。
以下是写入数据可能出现的情况:
case 1:
空闲时间处于最中间,写入 160 个数据需要花费 200 个时钟周期,这是写入数据最慢的极端情况。

case 2:
空闲时间处于每 100 个时钟周期的最开始,写入 160 个数据需要花费 200 个时钟周期。

case 3:
空闲时间处于每 100 个时钟周期的最末尾,写入 160 个数据需要花费 180 个时钟周期。

case 4:
写入的数据集中在最中间,写入160个数据需要花费 160 个时钟周期,这是写入数据最快的极端情况。

case 5:
空闲时间随机分布在 160 个写入数据之间,写入 160 个数据需要花费 200 个时钟周期。

下图是对各种情况的总结:
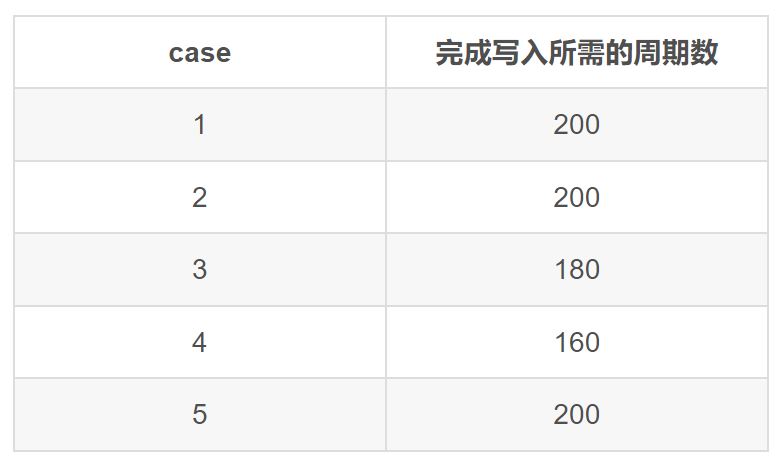
为了获得更安全的 FIFO 大小,我们需要考虑数据的最坏情况,在考虑中通过 FIFO 传输以避免数据丢失。
对于最坏的情况,写入和读取之间的数据速率之间的差异应该是最大的。因此,对于写操作,应考虑最大数据速率,对于读操作,应考虑最小数据速率。
写入的最大数据速率为 case 4 所示,160 个时钟周期可以写入数据 160 个。
就以 160 个时钟周期计算读取速率,读取的数据速率为 8 个数据/10 个时钟周期,在 160 个时钟周期可以读取的最少数据为 128。
因此 FIFO 的最小深度 = 160 – 128 = 32
情况10:
规格可以以不同的方式给出(了解规格在这里很重要)
给定以下 FIFO 规则,FIFO 需要多深才能防止下溢或溢出?
频率 (clk A) = 频率 (clk B)/4
周期 (en_B) = 周期 (clk_A)*100
占空比 (en_B) = 25%
解答:
可以假定一些数据:
假设 clk_B 的频率 = 100MHz
则 clk_A 的频率 = 100MHz /4 = 25MHz
在给出的规范中,突发长度是间接指定的。突发长度为 100
写入一个数据项所需时间 = 1 / 25MHz = 40ns
写入突发中的所有数据所需时间 = 40ns * 100 = 4000ns
由于 en_B 的占空比为 25%,所以读取的时间为 = 4000ns * 0.25 = 1000ns
所以 FIFO 需要保存剩余 3000ns 写入的数据量 = 3000ns / 40ns = 75
因此 FIFO 的最小深度为 75