一、概述
快速傅里叶变换(FFT)在雷达信号处理中扮演重要角色，我个人认为，如果FFT的在雷达信号处理中的地位是第二，没有哪个敢说是第一。
本文主要解释如何用FFT精确地测量信号功率（signal power），在时域中计算信号的功率非常容易，当信号中存在其他不同频率的信号分量和宽带噪声时，可以在频域中单独测量这些成分的功率或者测量它们之间的信噪比(SNR)。
由于FFT变换过程中采用加窗等诸多操作会带来的误差，引起幅度增益损失，故直接对信号进行FFT并不能获得准确的信号功率。这篇文章主要描述不同的影响因素，以及可以如何被避免或者补偿，文章的最后会详细说明如何通过FFT精确的测量信号和噪声的功率。
二、基本原理
在深入了解细节之前，这里先给出实信号（因为它们在现实世界中经常出现)的 FFT 的一些基础知识,。
2.1 实信号FFT
假设实信号通过算法1的N点FFT变换成频谱间距(bin)为
的功率谱。实信号的FFT变换频谱是对称的，所以频谱的前半部分就包含了频谱中所有的必要信息，在实际分析过程中可以直接忽略后半部分。
算法1：
input: N real time domain samples (time_signal)
twosided_fft = (1/N) * abs( fft(time_signal,N) ); % do fft
onesided_fft(1) = twosided_fft(1); % copy DC bin
onesided_fft(2:N/2) = 2 * twosided_fft(2:N/2); % double other bins
power_fft = onesided_fft.^2; % convert from RMS to power
output: N/2 point power spectrum
为了符合实际情况，需要对频谱中除了（第一个bin）直流分量以外的其他值乘2，通过这样变换之后得到了FFT产生的RMS（root mean squared均方根）谱。
注：假设原始信号的峰值为A，那么FFT的结果的每个点（除了第一个点直流分量之外）的模值就是A的N/2倍。而第一个bin就是直流分量，它的模值就是直流分量的N倍。
再将得到的结果进行平方就得到了信号的功率谱，需要注意的是，尽管信号经过的N点FFT变换，但由于只保留了一半的结果，所以功率谱中只有N/2个点的数据。
如果时域信号代表电阻器 R 上的电压，则算法1的输出可以转换为对数( dBm)，转换公式如下所示：
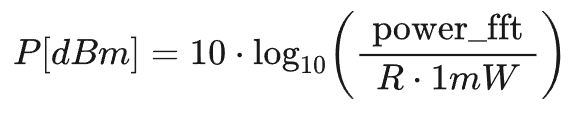
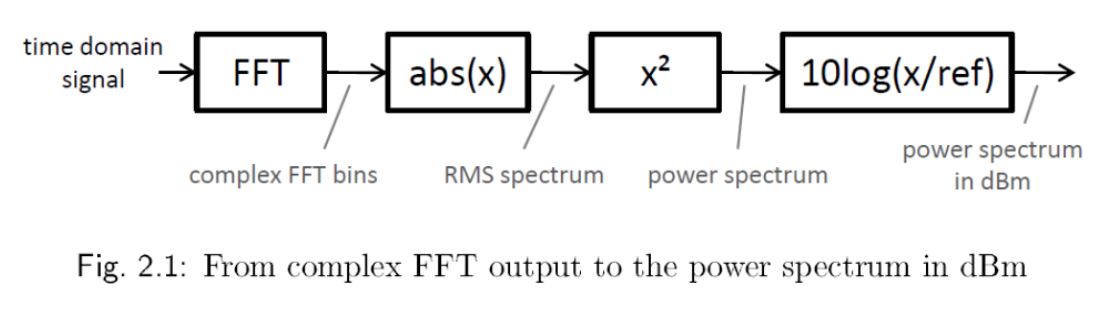
所有计算步骤的概述如图 2.1 所示。
三、FFT变换中的误差分析
下文中将会对FFT变换引起的幅值误差进行描述，有些误差只影响窄带信号（例如：sine信号），另外一些对宽带信号和噪声都有影响。
3.1频谱泄漏（leakage）
频谱泄漏是信号能量分布（弥散）在许多频率bin中的现象，单频信号并不表示为单个尖峰，而更像是一个宽阔的凸起，如图 3.1 所示。
注：即FFT进行的是离散傅里叶变换，在频谱上也仅仅在fs/N上有意义及存在数值。
发生频谱泄漏的根本原因是：FFT 仅分析信号的（短）片段信号（N 个样本），但是通常想要从这个片段信号中提取有关整个信号的信息。而实际上FFT输出是一个由N点样本重复拼接起来的信号，通常来说这个拼接信号在边界点处不连续，因此FFT的输出频谱代表的并不代表“真实”信号。
对于信号来说，只有那些周期（或者周期的倍数）刚好和信号长度相同时，频谱泄漏才不会发生。虽然理论上可以根据信号调整ADC转换器的采样频率得到，但在实际中不容易控制，因此假设在分析过程汇总信号泄漏总是存在的。
为了抑制泄漏，可以在对信号进行FFT变换前进行加窗。常用的窗函数有汉宁窗（hann）（最常使用），flattop 窗（为了进行准确的幅值测量）或者不加窗，或者说加矩形窗（针对噪声测量）。加窗后频谱的泄漏量可以通过最高旁瓣（highest sidelobe）的dB值和dB/octave的衰退量（fall off）进行测量。
对于精密测量来说，只要泄漏没有影响频谱成分例如：spurs（毛刺）和noise（噪声），就不算是一个大问题。
3.2相干功率增益（Coherent power gain）
如下图所示，对一个信号进行加窗操作之后将会减少信号在时域上的幅值，尤其是在窗函数的左右边界。
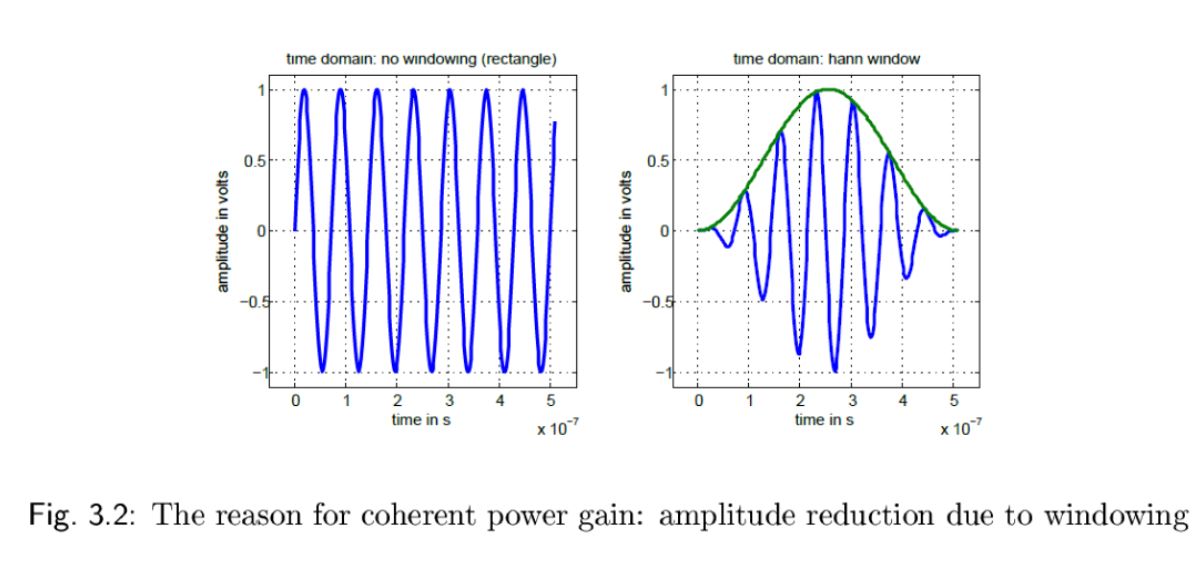
这种幅度的减小会引入幅度误差，称为相干功率增益（CPG）。增益这个词可能会产生误导，因为 CPG 实际上描述的是信号功率的损失。图 3.3 显示了在实践中如何通过使用窗口来降低 FFT 幅度，每个窗口都有一个固定或典型的 CPG。
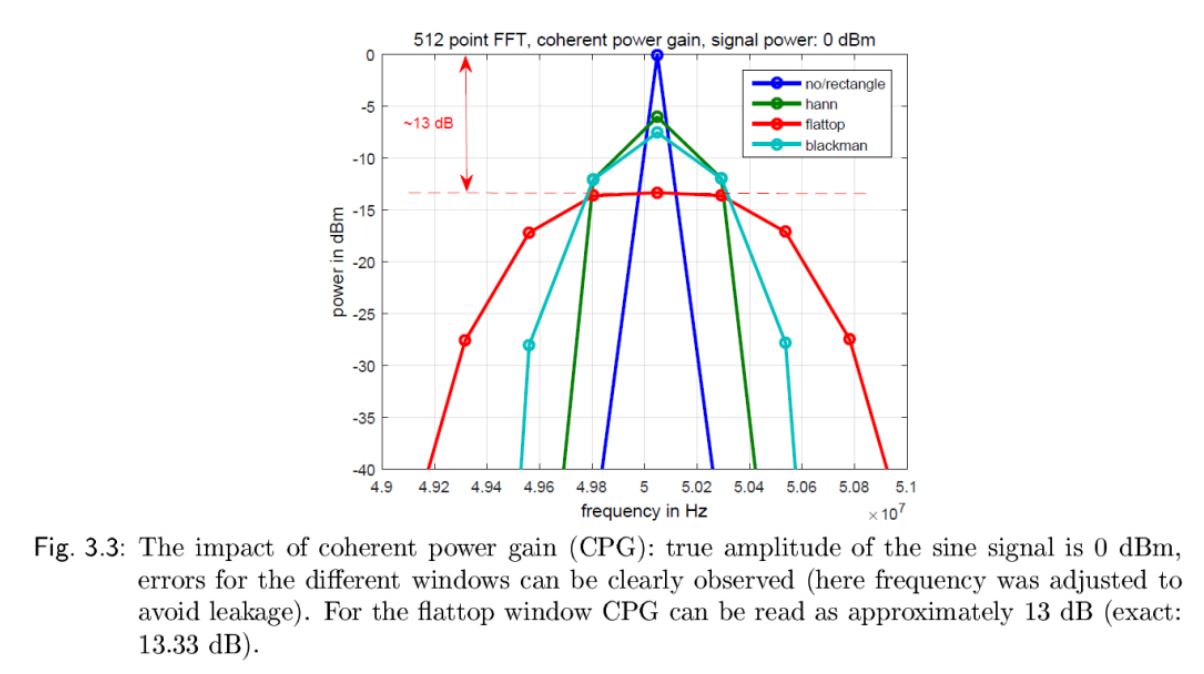
常用窗函数的CPG值可以在3.6节中找到，只需将此增益添加到 FFT 输出即可补偿功率降低。如果没有使用窗函数（或者说使用了矩形窗），那么就不存在相干功率损失，CPG值为1或者0dB。
3.3栅栏损失（Scalloping loss or picket pence effect）
由于FFT变换的结果在频域上是离散的，那么信号的频率就可能落在两条谱线之间。如果发生了这种情况，那么显示的功率就会因为功率被分散到两根谱线上而减少，这部分损失叫做栅栏损失，损失计算公式如下：
其中，N是FFT长度，L是信号样本数，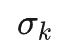 
是偏离谱线的索引长度(跨bin间距)，大小位于[-0.5，0.5]之间，即信号频率落在两条谱线之间，在正中间是损失最大，不同窗函数栅栏损失有所不同。
频率的离散化也可以被认为是对相应的连续频谱进行采样，根据连续频谱的采样频率，FFT 频谱看起来会有所不同，如图 3.4 所示。
左图中信号频率基本落在一条谱线上：幅值损失小并且泄露很少。而右图的信号频率落在了两条谱线之间：信号功率被分散，幅值降低并且泄漏很大。
对于每种窗函数，栅栏损失不能用一个确定的值来进行描述。因此它不能简单地用一个参数去补偿幅值损失。栅栏损失一般来说对于每种频谱分量的大小一般是不同的，其很大程度上依赖于信号频率、采样频率和谱线数目。但是可以计算出最大栅栏损失，即当信号频率刚好落在两条谱线之间的情况。
除此以外，还有两种方式可以用来避免栅栏损失：
（1）使用flattop window，一般只产生很小的最大栅栏损失（<0.02dB）；
（2）根据信号频率，合理设置采样频率，这种方法同样可以用来避免频谱泄露
3.4 FFT处理增益（FFT processing gain）
处理增益可以降低背景噪声基底，原理如下：FFT变换可以看做是将信号通过多个窄带滤波器（梳状滤波器），每一个滤波器的频率间隔为 
，并确定了每个滤波器的功率输出。当谱线数量N（或者说滤波器数量）增加时，滤波器变窄并且相应每条谱线上的功率会变小，如图3.5所示，随着FFT点数变多，底噪变得平坦很多。
处理增益PG（processing gain）准确地描述了这部分减少量。若N翻倍，则
变为原来的一半，噪声基底降低3dB，这将影响如噪声等宽带信号在功率谱上的幅度。由于处理增益影响，FFT谱上的噪声基底将会比原来更低，处理增益可以按下式进行计算：
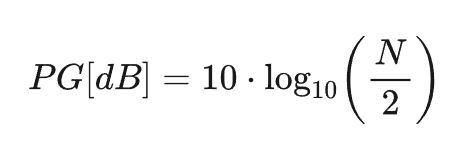
并且可以加到噪声基底上去补偿这部分效应，为了准确测量噪声基底水平可以将多个FFT变换结果进行平均以减少幅度波动（如图3.5右侧所示）
3.5等效噪声带宽（Equivalent noise bandwidth ENBW）
根据所应用的窗函数，单一谱线上所积累的噪声量会有所不同，这种不同所依据的就是ENBW。如果使用了一个非矩形窗，那么这种现象就会导致噪声基底的升高。为了补偿这部分效应，需要从基底噪声中减去一个修正系数，这个修正系数可以通过不同窗函数的ENBW进行计算。
3.6 总结
FFT误差来源如下图所示：
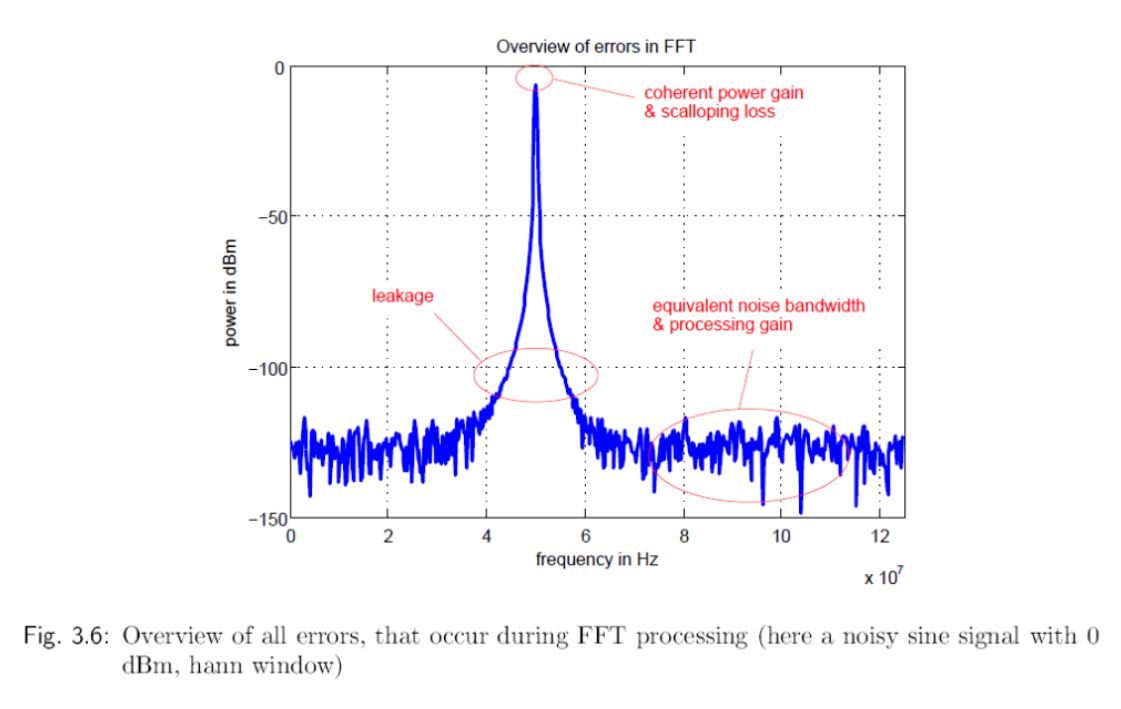
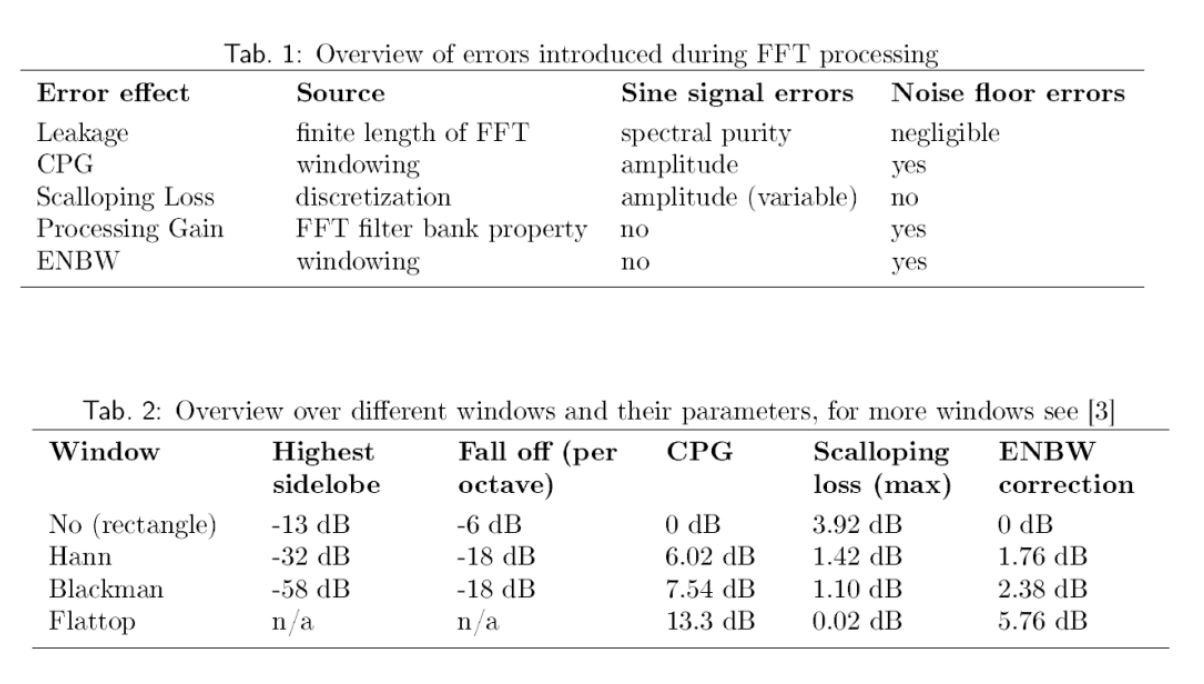
同时，表1展示了FFT 处理期间引入的误差概述。表2展示不同窗口及其参数的概述。
四、FFT精确测量
如果上述因素被正确地考虑在内，那么信号就可以通过FFT进行准确地测量。下面以一个受到噪声干扰的正弦函数进行说明。
相干功率增益可以通过Tab.2中获取，需要注意的是栅栏效应并不是一个常数。如果信号能量被单根谱线捕捉到了，那么可以记做0dB，如果信号能量刚好被两根谱线平分，那么其数值可以从Tab.2中查看最差情况。如果需要准确的数值而信号又不在谱线中间，那么最简单的办法就是使用flattop窗函数，或者直接用公式计算。
4.2噪声和其他宽带信号
这里必须区分两种信号类型：白噪声，即在整个频带上具有恒定功率密度的噪声，以及任意噪声或宽带信号。
4.2.1 Reading the average noise（白噪声）
4.1 正弦信号和窄带信号
相干功率增益可以通过Tab.2中获取，需要注意的是栅栏效应并不是一个常数。如果信号能量被单根谱线捕捉到了，那么可以记做0dB，如果信号能量刚好被两根谱线平分，那么其数值可以从Tab.2中查看最差情况。如果需要准确的数值而信号又不在谱线中间，那么最简单的办法就是使用flattop窗函数，或者直接用公式计算。
4.2噪声和其他宽带信号
这里必须区分两种信号类型：白噪声，即在整个频带上具有恒定功率密度的噪声，以及任意噪声或宽带信号。
4.2.1 Reading the average noise（白噪声）
为了最后得到准确的结果，显示的本底噪声必须被准确地测量。然而，由于噪声的随机性，想要达到这个目标比较困难。为了获得准确的本底噪声，一般有两种解决方法：
（1）FFT averaging：平均多次的FFT变换结果来降低噪声的随机性；
（2）Bin averaging：对单次FFT变换得到的谱线进行平均（排除掉代表直流分量和其他不需要成分的谱线），这一部分在下面的章节中将会进行详细说明。
4.2.2 Summing of FFT bins（任意噪声和宽带信号）
将FFT变换的谱线加起来是一个处理所有噪声和宽带信号的很好的方法。除了按照上述方法确定本底噪声，可以将包含待测信号分量的频率谱线简单相加。需要注意的是，相加的值是线性值（不是dB）并且修正增益不需要加入其中，因为这些增益已经被考虑在相加过程当中了。
这种方法的优点是所需要的谱线可以按照需求进行挑选，进行方便的测量。
4.3示例
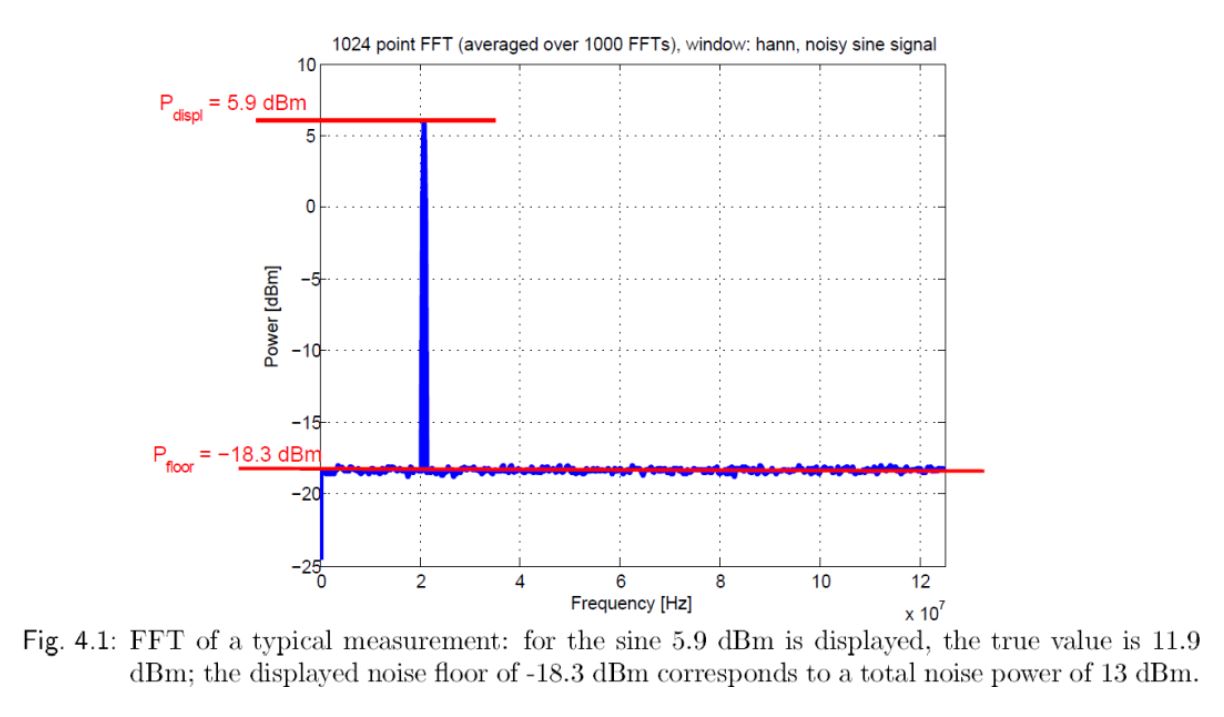
如上图显示了一个典型的受白噪声干扰的正弦波的FFT变换结果。因为分析过程中使用了汉宁窗，所以显示的功率谱并不是真实的功率表谱，显示的正弦信号功率为5.9dBm，使用前面提到的公式可以得出正弦信号真实的功率谱，如下所示。
其中，CPG为6dB，因为谱峰基本落在单一谱线上，所以栅栏损失定义为0dB。
本底噪声也可以通过显示值进行计算，如下所示其中，CPG为6分贝，1024点FFT的处理增益为27.1dB，ENBW的修正系数约为 -1.8 dB）
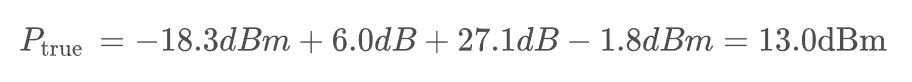
图4.1的测试信号是由 11.94 dBm 正弦信号加上 13.02 dBm 噪声信号合成的，可以看出计算的结果和理论的结果基本相同。
参考资料：Exact Signal Measurements using FFT Analysis
