本文转载自: 雷达通信电子战的微信公众号
目前,用来量化ADC动态性能的六个技术指标分别为SINAD(信号与噪声失真比),ENOB(有效位数),SNR(信噪比),THD(总谐波失真),THD+N(总谐波失真+噪声),和SFDR(无杂散动态范围)。
量化ADC失真和噪声的方法有很多,这些方法都是利用基于FFT分析的测试装置,如图1所示。
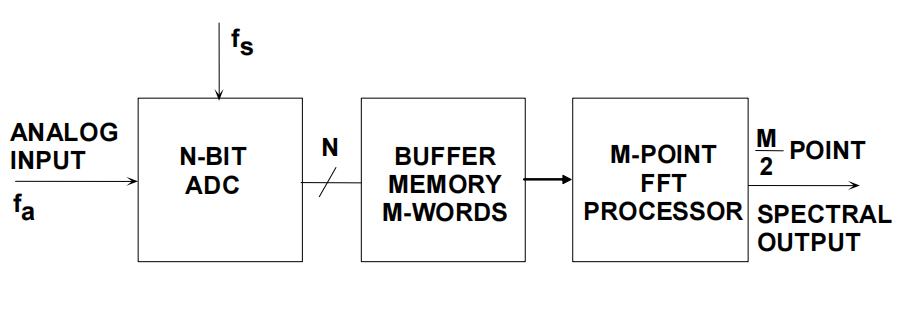
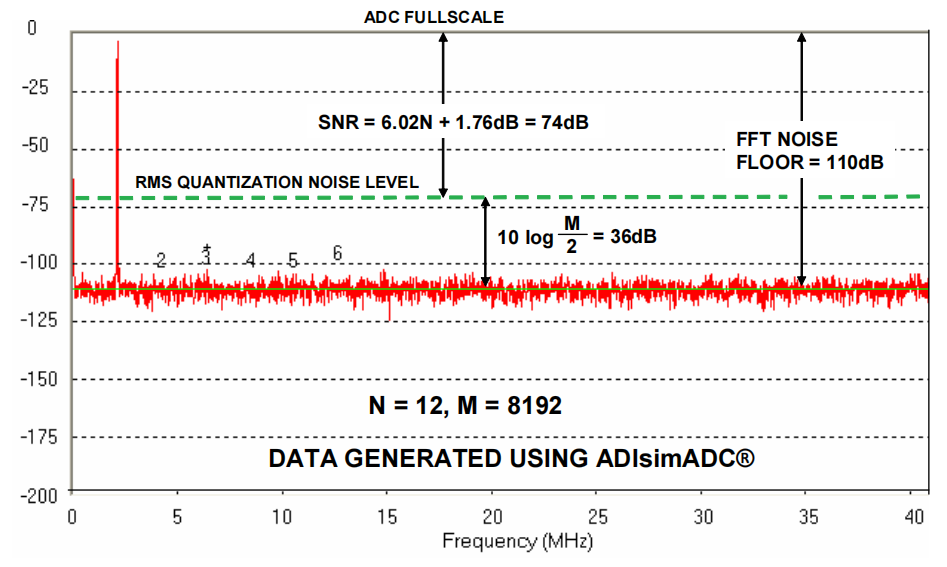
图2中FFT的数据表示的是5个独立的FFT的平均值。请注意,对若干个FFT的数据进行平均并不会影响本底噪声的平均值,其只是用来“平滑”每个频率窗口中随机变化的振幅。
谐波失真通常以dBc(相对于载波的分贝值)为单位,尽管在音频应用中其可能表示为百分比。它是信号的有效值与有关谐波的均方根的比值。谐波失真通常是以接近满量程的输入信号进行测量(通常会比满功率低0.5~1dB,避免削波),虽然它能在任何电平下进行测量。对于远低于满功率的输入信号,由于转换器的差分非线性(DNL)将产生其它失真产物,而不是直接谐波,可能限制转换器的性能。
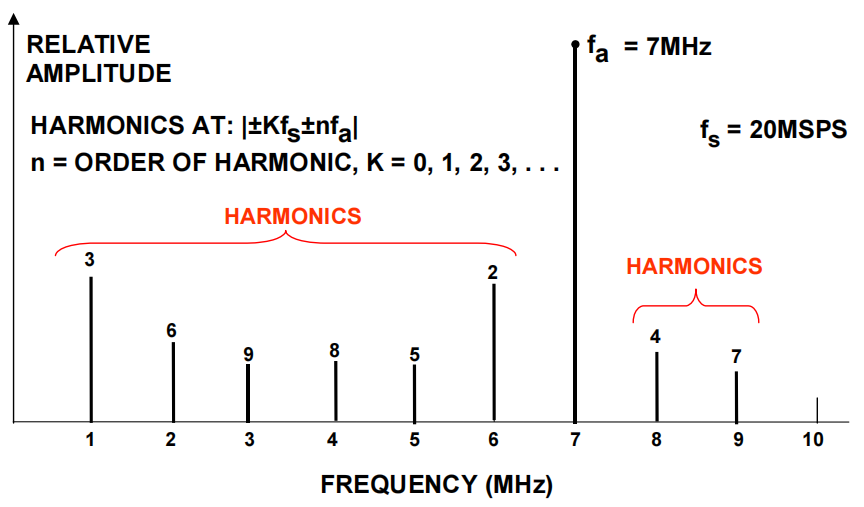
总谐波失真+噪声(THD+N)是基波信号的有效值与其谐波信号和的平方根的平均值加上所有噪声分量(包括dc分量)的比值。其中,必须指定被测量噪声的带宽。对于FFT,其带宽为dc至fs/2(如果测量带宽是dc至fs/2(Nyquist带宽),那么THD+N与SINAD相等,详见下文)。但是,需要注意的是,在音频应用中测量带宽不一定是Nyquist带宽。
无杂散动态范围(SFDR)
无杂散动态范围(SFDR)是输入信号的有效值与频谱中最差杂散信号的有效值的比值。最差的杂散信号有可能是原始信号的谐波。在通信系统中,SFDR是一个十分重要的指标,因为它代表了能从一个较大的干扰信号(阻塞器)中区分出的最小信号。SFDR可以相对于全量程(dBFS),或者相对于实际的信号振幅(dBc)进行说明。图4形象地表示了SFDR的定义。
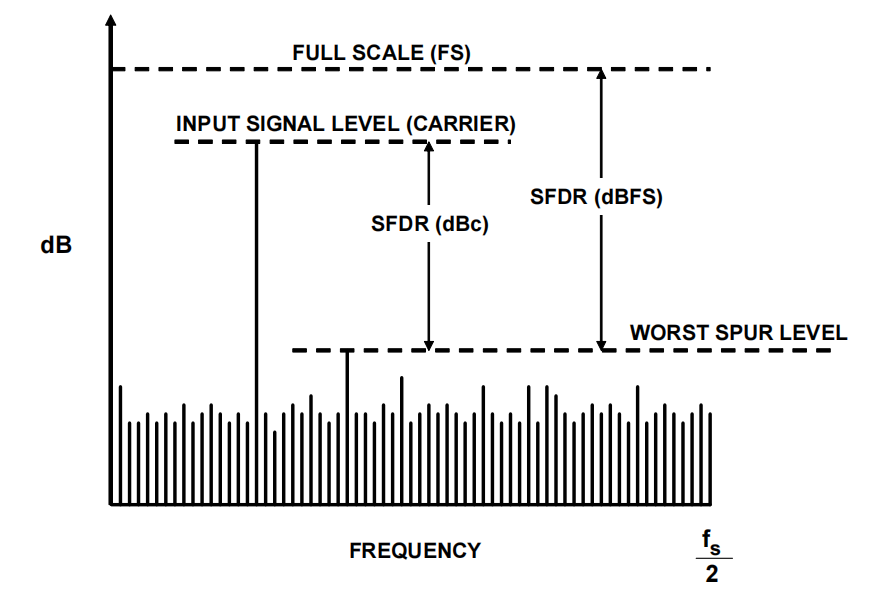
图4 无杂散动态范围(SFDR)
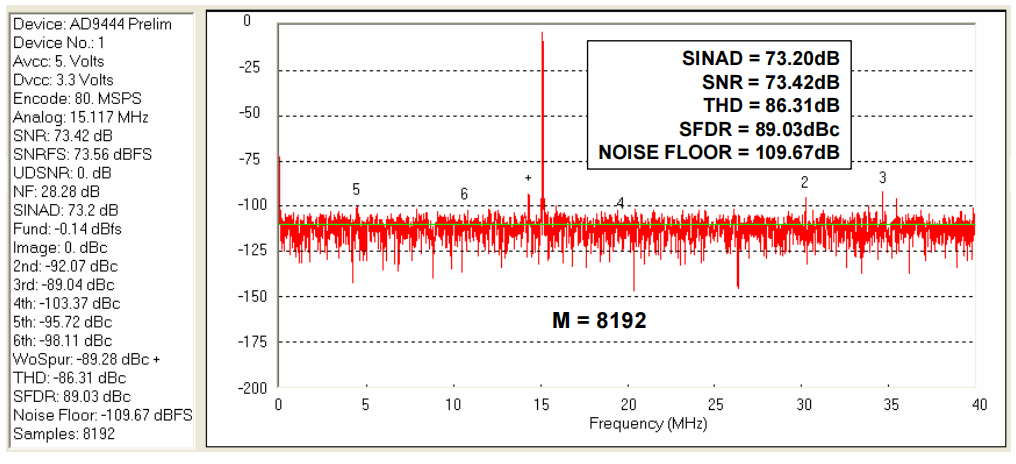
图5 AD9444,采样率为80MSPS的14位ADC,fin=95.111MHz,fs=80MSPS,5个独立的FFT的平均值
SINAD,SNR,ENOB
SINAD和SNR值得特别关注,因为不同的ADC制造商对两者的确切含义仍有一定的差异。信号与噪声失真比(SINAD,或者S/(N+D))是信号振幅的均方根与所有其他频谱分量的和的平方根的平均值的比值。其他频谱分量包括谐波,但是不包括dc分量。
SINAD能够很好地反映一个ADC的整体动态性能,因为它包括构成噪声和失真的所有分量。SINAD通常是根据输入信号不同的振幅和频率绘制的。当给定输入信号的振幅和频率时,SINAD等于THD+N,前提是两者测量噪声的带宽是相同的,均为Nyquist带宽。AD9226,采样率为65MSPS的12位ADC的典型图如图6所示。
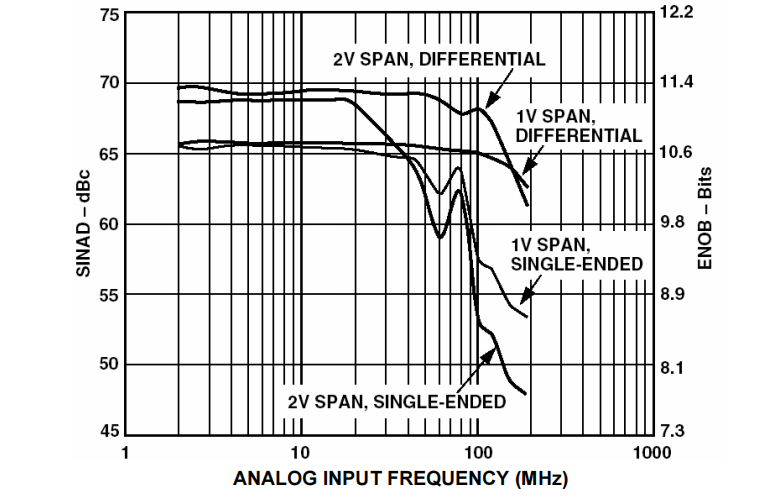
图6 AD9226,采样率为65MSPS的12位ADC的SINAD和ENOB曲线图,适用于各种全量程(范围)的输入
SINAD曲线图表明,由于高频率失真,ADC的交流性能随之下降,一般绘制远高于Nyquist频率的曲线图,从而可以评估器件在欠采样应用时的性能。像这样的SINAD曲线图对于评估ADC的动态性能十分有用。利用理想的N位ADC的理论SNR与有效位数(ENOB)的关系:

修正系数本质上是将ENOB的值相对于满功率的信号进行“归一化”,而不考虑实际信号的振幅。
信噪比(SNR,有时也称作无谐波的信噪比)也能通过FFT数据进行计算,与SINAD一样,只是在计算过程中不考虑信号谐波,只考虑信号噪声。实际上,只需将前5阶谐波排除在外,因为它们占谐波的主要部分。当输入信号的频率较高时,信噪比曲线会下降,但是一般不会像SINAD曲线一样下降得那么快,因为在计算的过程中不包含信号谐波。
某些ADC数据表笼统的将SINAD称作SNR,因此,当你使用这些参数时必须特别注意,应当准确理解制造商所表达的含义。
SINAD,SNR,和THD间的关系
SINAD,SNR,和THD之间存在相应的数学关系(假定,在所有的测量中,输入信号具有相同振幅和频率)。在接下来的方程中,SNR,THD,和SINAD的单位都是dB,并通过实际的数学比率S/N,S/D,和S/(N+D)计算得出,如下所示: