作者:张海军,文章来源:傅里叶的猫
今天来看这篇论文:论文讨论了一种方法来更有效地利用现代FPGA中集成的数字信号处理器(DSP)资源。具体来说,该方法专注于如何在单个DSP块中进行低精度算术运算的打包,以提高计算密集型算法的性能、功耗和面积效率。
引言
由于FPGA中的DSP资源往往被设计成支持较大的位宽运算(例如48位累加器或18x27位乘法器),当应用于低精度数据处理时(如图像处理或机器学习中常见的量化数据),这些资源可能会出现利用率不足的问题。
为了解决这一问题,论文提出了一种方法,能够在单个时钟周期内在一个DSP块上同时执行四个4位乘法操作。这种技术被称为“打包”(Packing)。此外,论文还对该方法进行了推广,使其适用于任意位宽和任意数量的乘法操作。研究还指出,之前提出的打包方法会导致一定的误差(平均绝对误差MAE为0.37),并且解释了这些误差产生的原因以及如何进行修正。
论文还介绍了一种称为“Overpacking”的新近似方法,这种方法可以在牺牲一定精度的前提下(MAE为0.47),在一个DSP块中实现更多的乘法操作,例如可以将六个4位乘法操作挤入一个DSP块中,相较于之前的方法提高了利用率。
目前已有的研究
下面的内容具体可查看论文中的参考文献:
Huang等人提出了一种在单个DSP切片上实现平行乘法的方法。
在Xilinx UltraScale FPGAs的DSP48E2上,这种方法可以实现两组乘法(w0·a0=r0 和 w1·a1=r1)以及一个乘积累加结果(r2=w0·a1+w1·a0)。
为了达到最大利用率,w0 和 w1 必须是4位宽,而 a0 和 a1 必须是5位宽,这导致结果 r0, r1 的位宽为9位。
Mert等人提出了一种方法,可以在单个DSP上实现两组乘法(c0·a0=r0 和 c1·a0=r1)。
其中 c0 和 c1 必须是常数,而 a0 是相同的变量输入。
这种方法要求在电路合成前将常数分解为移位操作。
但在许多应用场景中,乘法操作数在运行时变化,使得这种方法不可行。
他们扩展了Mert等人的方法,通过使用查找表技术来存储分解后的常数。
查找表允许在运行时改变这些常数。
此外,还提出了一种近似计算技术来减少由查找表带来的巨大开销。
在Xilinx白皮书中提出了一种方法,可以在单个DSP上实现两组乘法(w0·a0=r0 和 w0·a1=r1),这种方法称为INT8-packing。
所有输入操作数都有8位宽,产生两个16位结果。
类似的方法也被Lee等人提出过。
另一个Xilinx白皮书提出了一种方法,可以在单个DSP上实现四组乘法(w0·a0=r0, w1·a0=r1, w0·a1=r2, w1·a1=r3),这种方法称为INT4-packing。
输入操作数 w0, w1, a0, a1 都有4位精度,产生四个8位结果。
综上所述,这些方法试图解决DSP资源在处理低精度数据时的利用率问题,通过在单个DSP上执行多组乘法来提高资源利用率。然而,每种方法都有其局限性,如特定的输入位宽要求、对常数的需求或是对输入数据的限制。
论文中的新方法
论文主要就是研究如何在单个DSP块中实现多个低精度乘法运算的技术:
INT4-Packing简介
INT4-Packing是一种技术,它可以在单个DSP块中同时执行四个4位乘法运算。
这种技术通过重新排列输入值来实现,使得四个独立的乘法可以在单个DSP块中同时完成。
输入向量a和w各有两个元素,分别为a0和a1,以及w0和w1。
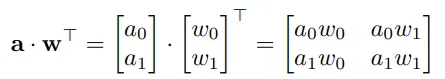
a0和a1是4位无符号整数,而w0和w1是4位带符号整数。
通过将输入重新排列,可以将这四个乘法运算(a0w0, a0w1, a1w0, a1w1)压缩到一个DSP块中。
重排的方式是通过位移操作实现的,例如a1 * 2^11 + a0和w1 * 2^22 + w0。
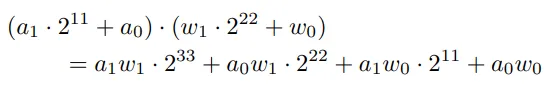
映射到DSP48E2
a0映射到B端口,偏移量为0。 a1也映射到B端口,但是偏移量为11,这相当于a1 * 2^11。 w0映射到预加器端口A,因为它是带符号的,所以它的符号位必须扩展到所有最高有效位(MSBs)。 w1同样因为是带符号的,不能映射到与w0相同的端口,因此它被映射到预加器端口D,偏移量为22。 四个乘法结果可以从P端口提取出来,它们之间通过3位的填充位(δ=3)隔开,这样在级联DSP时可以正确地累积结果。
INT-N泛化
INT-N是一种架构无关的打包技术,它可以生成不受目标DSP约束影响的乘法打包配置。
这种技术允许用户定义输入向量a和w的元素数量,以及每个元素的位宽。
输入向量a和w的偏移量分别存储在集合aoff和woff中,位宽分别存储在awdth和wwdth中。
结果向量r包含外积a·w>的结果,其偏移量和位宽分别存储在roff和rwdth中。
偏移量决定了输入向量元素与结果向量元素之间的关系,可以用数学公式表示,即roff,j·|aoff|+i= aoff,i+ woff,j。
举例来说,INT4-Packing的配置为:Padding δ= 3, wwdth= awdth={4, 4}, rwdth={8, 8, 8, 8}, woff={0, 22}, aoff={0, 11}, roff={0, 11, 22, 33}。
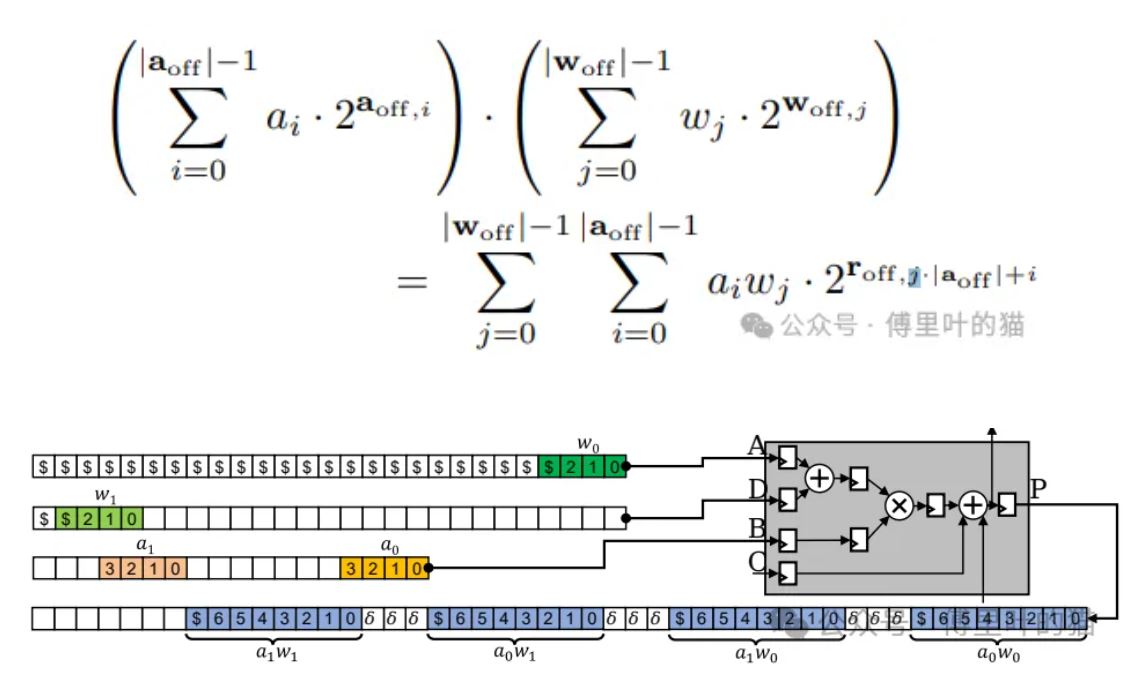
通过这种方式,INT-N不仅提供了INT4-Packing的泛化版本,而且也适用于其他类似的情况,比如INT8-Packing。这种技术允许设计者根据特定的应用需求灵活地配置DSP资源,以实现更高的硬件利用率和更好的性能。
接下来作者对乘法打包技术进行了详细的错误分析,并提出了一种新的方法称为“过打包(Overpacking)”来进一步提高DSP资源的利用效率,还介绍了一种将多个小位宽加法操作打包进FPGA DSP模块中的48位累加器的方法。
ERROR ANALYSIS OF MULTIPLICATION PACKING
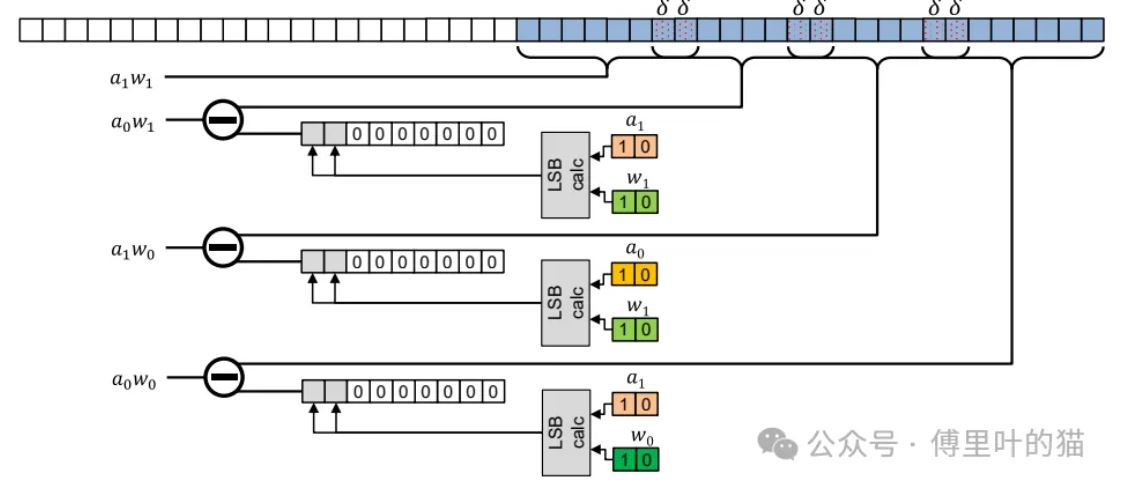
乘法打包技术,特别是由Xilinx提出的INT4打包技术,在实际输出和预期输出之间存在一定的误差,其中一些实际输出比预期输出小1。 错误来源于从结果位串中提取各个乘法结果时隐含执行的右移操作。由于右移操作对于有符号整数总是向下取整,这就导致了结果偏负无穷方向的偏差。 对于INT4打包技术,这种偏差导致约37%的输入组合产生误差。 论文提出了两种错误校正方案: 全部错误校正:需要额外的硬件资源(查找表LUTs和触发器FFs),但可以完全消除误差。 近似错误校正:只使用DSP内部的累加器,不增加额外硬件成本,可将误差概率从37%降低至3%。
OVERPACKING
过打包是一种新方法,允许在一个物理DSP输入上打包更多的逻辑值,从而得到部分错误的结果。这种方法允许在一个DSP上执行六次4位乘法,相比文献中的四次4位乘法提高了50%的利用率。
过打包通过设置偏移量δ(例如δ=-2)来实现,这会使得高位结果被低位结果污染。
论文提出了一种硬件解决方案,通过对低位污染进行修正来改进结果。这种修正可以通过计算低位污染位并从中减去它们来实现。
这种修正方案的成本随着需要修正的低位数量的增加而指数级增长。然而,修正低位1和2位是非常廉价的,因此大部分的昂贵乘法仍然在优化过的DSP中完成,而廉价的修正逻辑则用来修正高位的错误。
过打包引入的大误差由于低位的污染导致,但对于某些应用如卷积神经网络(CNNs),这种误差是可以接受的,因为它们对量化和近似具有内在的鲁棒性。

ADDITION PACKING
在尖峰神经网络(SNNs)中,主要的计算操作是加法,这与标准神经网络(NNs)基于乘积累加操作不同。
提出了一种方法来将多个小位宽的加法操作打包到一个DSP的48位累加器中,这对于减少FPGA上的查找表(LUT)和触发器(FF)资源的需求特别有用。
论文展示了如何在一个DSP中实现五个9位加法器,这表明了该方法在实际应用中的可行性。
为了评估打包方案的有效性,引入了一个名为打包密度ρ的度量,ρ定义为被乘法结果占用的位数除以DSP总输出位数。
不同的打包技术(如INT-N和过打包)在DSP资源利用率方面有不同的表现,过打包在利用DSP资源方面显示出优势,尤其是在增加乘法操作的数量和位宽方面。
这些方法和技术共同提高了FPGA中DSP资源的利用效率,特别是在处理低精度算术运算时,如图像处理和机器学习应用。
EXPERIMENTS AND RESULTS
在实验部分,论文通过一系列测试验证了所提出的不同打包技术的效果,包括INT4-Packing、Overpacking以及添加打包方案的性能。
测试条件:所有测试均使用4位操作数进行四次乘法运算。 测量指标:使用平均绝对误差(MAE)和错误比例(EP)作为评估标准,以比较实际输出与期望输出之间的差异。 INT4-Packing:原始方法导致平均绝对误差为0.37,错误比例为37.35%,最坏情况误差(WCE)为1。 INT4-Packing全纠错:通过增加额外的查找表(LUTs)和触发器(FFs),可以完全消除误差,但这会增加硬件开销。 INT4-Packing近似纠错:使用DSP内部的累加器进行纠错,可以显著降低误差,平均绝对误差为0.02,错误比例降至3.13%,最坏情况误差仍为1。 Overpacking:该方法允许在一个DSP上执行更多的乘法操作,但以引入误差为代价。例如,当偏移量δ=-2时,平均绝对误差为37.95,错误比例为58.64%,最坏情况误差为194。 MR-Overpacking:这是Overpacking的一个变体,它引入了更大的误差以换取更高的资源利用率。例如,当偏移量δ=-2时,平均绝对误差为0.47,错误比例为41.48%,最坏情况误差为20。 添加打包方案:该方案允许在一个DSP中执行五个9位加法器,没有使用保护位,平均绝对误差为0.51,错误比例为51.83%,最坏情况误差为1。
CONCLUSION
在结论部分,论文总结了所提出的DSP-Packing方法的优势及其在小位宽乘法中的应用。
INT4-Packing的局限性:包括固定的操作数位宽、固定的乘法操作数数量以及固定的填充位(δ=3)。 INT4-Packing的误差:虽然误差相对较小(平均绝对误差为0.37),但会导致结果偏负无穷方向的偏差,这对某些应用可能是个问题。 打包方案的泛化:所提出的技术可以泛化到任意位宽和任意数量的乘法操作,受限于DSP的架构。 Overpacking:这是一种近似方法,允许在一个DSP中执行更多乘法操作,但会引入更大的误差(例如,当δ=-2时,平均绝对误差为0.47)。 添加打包方案:对于尖峰神经网络等应用,可以有效地利用DSP的48位累加器来执行多个小位宽加法操作。 打包密度ρ:这是衡量打包效率的一个指标,定义为被乘法结果占用的位数除以DSP总输出位数的比例。
总体而言,论文提出的方法有效地提高了FPGA中DSP资源的利用率,尤其是在处理低精度数据时,如图像处理或机器学习应用中的量化数据。这些技术不仅提高了DSP的利用率,还提供了灵活性和适应性,以满足不同应用的具体需求。
该论文中的公式和图片较多,本篇博客总结出来内容可能并未能完整的表达论文中的所有内容,建议有兴趣的读者可以看原文。
