本文只涉及各种傅利叶之间的概念关系,不考虑数学严谨性。
一张图理解各种傅利叶
from Understanding Digital Signal Processing. Richard G. Lyous
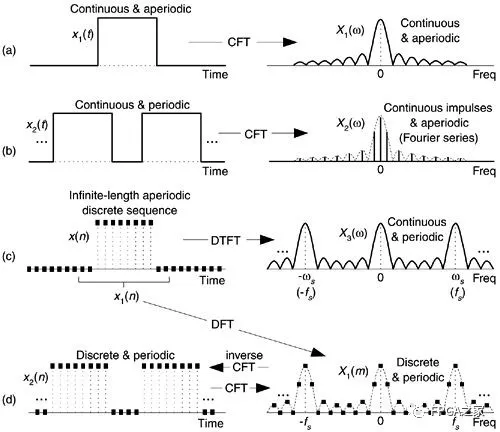
a为连续时间非周期信号的傅利叶变换,频谱为连续非周期谱;(CFT)
b为连续时间周期信号的傅利叶级数,频谱为离散非周期谱;(FS)
c为离散时间非周期信号的傅利叶变换,频谱为连续周期谱;(DTFT)
c为离散时间周期信号的傅利叶变换,频谱为离散周期谱;(CFT)
上面的描述有些苍白,那怎么理解这张图呢?
就像电容电感有对偶一样,时域和频域也有对偶的现象。离散时间信号可以看作是对连续时间信号的抽样;而离散频谱也可以看作是对连续频谱的抽样。那么上面四组图的规律就是:
1. 时域的周期化对应频域的抽样化,如(a)与(b),或(c)与(d);
2. 时域的抽样化对应频域的周期化,如(a)与(c),或(b)与(d);
对于这一点的进一步理解,有以下简单说明:
1. 最初的傅利叶级数的意义为任何周期信号都可以由一系列正弦信号加权叠加生成,即频域为一系列频率,频域不是连续的。而时域的非周期信号可以看作是周期信号将其周期T逐渐加大到无穷大,则频率间隔1/T逐渐减小到无穷小,即形成了连续的频谱;
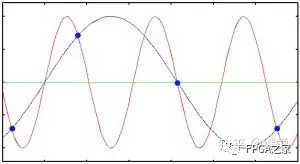
2. 对连续时间进行抽样,则频谱会受采样频率的影响,因为同样的采样数据可以对应不同频率的分量,如下图所示。即时域抽样过程使频域形成以采样频率fs为周期的周期频谱。
from ircam.fr
以上为理解思路,详细内容不缀述。
P.S.
DFT与离散时间周期信号的CFT等效。
各种傅利叶都有其适用范围,例如,因为计算只能处理离散的数据,所以只有DFT是数字计算机可以直接处理的傅利叶变换。
文章转载自:FPGA之家