来源:AI加速微信公众号
在上一篇介绍了如何将高维度卷积核拆分成低维度小卷积核,从而降低计算量的方法。本篇介绍的也是采用了降维的思想来加速网络推理,但是数学上采用了不同的方法。而且这篇文章提出的方法可以加速深度网络,其在vgg-16上进行了实验,获得了4倍的加速效果,而在imageNet分类中top-5错误率仅有0.3%升高。
1、原理
首先我们来看神经网络中的卷积运算的形式,对于任一个隐藏层,它有c幅输入图片,每幅图片都会和一个卷积核进行卷积运算。假设卷积核大小为kxk,那么就有c个卷积核。我们可以将图片沿着个数方向重新生成一个维度,图片就成了一个3D的张量,大小为hxhxc。卷积核为kxkxc,其在kxk方向进行划窗,而c方向进行求和。每个输出点实际上是kxkxc个乘法求和结果。这c个卷积核会输出一幅图片,如果隐藏层有d个节点,实际上是输出n幅图片。如果将kxkxcxd这么大的卷积核进行重新排列,排成一个d行,每行有kxkxc个数据,就称为了一个矩阵,我们令为W。那么输入图片排成一个向量,长度为kxkxc。用矩阵乘法可以表示为:
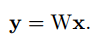
W为一个dx(kkc+1)的维度矩阵,多增加一个1是将bias加在末尾。但是有人会问一幅图片是hxh个点,现在仅在x向量中取了其kxk个点,那么其他的点如何计算呢?实际上其它点可以看做为多组x向量输入,在之后降维分解中都考虑在内。
从上述公式看出,计算量复杂度为O(dkkc)。文章中作者假设了y是一个低维度向量,也即可以用更少信息来表示y向量。这点和其他研究这不一样,cp分解中是直接考虑矩阵W的低秩行为,而作者实际上考虑了结果y的低维度表示。相比于cp可以综合考虑到x的低维度以及W的低秩行为,以及在后边还可以将非线性考虑进来,这是本篇文章可以用于更深网络的本质原因。
接下来作者重新表达y为:
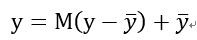
M是一个dxd的矩阵,秩为d’。y-是平均响应,其维度也为d’。但是这里作者为什么引入了y-并没有讲。我想和归一化有类似作用吧,可以纠正数据沿着网络传输的发散性。经过降维的后的y,其和x关系变为了:
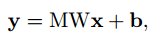
b是新生成的bias,为:
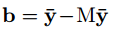
由于M的秩为d’,所以可以进行分解为:
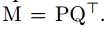
那么就有:

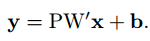
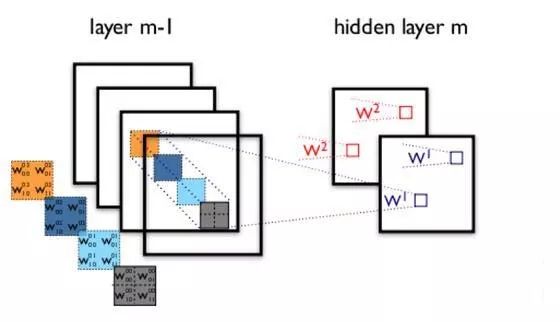
W矩阵变为d’x(kkc+1)大小,因此计算量降低为O(d’kkc)+O(dd’),因为O(dd’)很小,所以计算复杂度变为原来的d’/d。实际上是减小了神经网络中输入通道的数量,将输入通道减少拆分成两层网络,如图中所示。而CP分解的权重通道数没有变,而是减小了kxk方向维度。
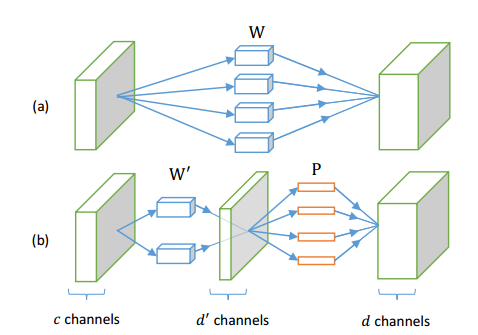
以上公式的导出都是基于y有较低的维数表达,实际中并不会有这样严格的数学性质,因为对于任意输入x,以及不同训练集训练出来的网络,我们不能保证y的维数实际低于d。所以这变成了一个近似问题,如何选择一个d’,同时使得新获得的参数的网络可以逼近最初结果。作者使用平方差来作为目标函数进行计算:

以上优化问题可以很容易获得解。实际上是寻找yyT的最大本征值,这类似于PCA方法。通过提取出排列在前几位最大的本征值,而剩余本征值设置为0来优化网络参数。最大本征值反应了表达y的信息的能力。然后通过一些矩阵变换就可以得到M矩阵。
上述方法很容易兼容非线性单元,因为考虑非线性单元后,优化目标变为:
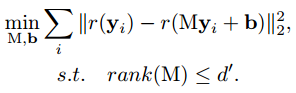
其中r为非线性函数,作者只考虑了ReLu函数的求解。以上目标函数很难求解,因此作者做了一些数学变换,将上述损失函数进行了松弛处理,即引入了z,重新表达为:

从中看出当lamda逼近无穷时,其目标函数等同于原始目标函数。通过上述方法,可以优化每一层的网络参数。因为每层网络的输出是下层输入,所以整个优化一层层传递下去可以完成整体网络优化。
2、结果
首先作者选择了一个10层网络进行试验,结果为:
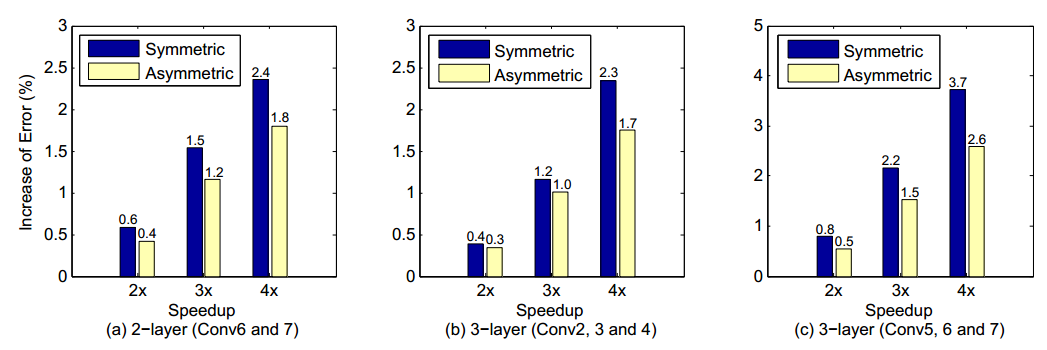
这里symmetric和asymmetric是作者进行非线性优化时,分别使用了原始的输入结果和近似输入结果来进行的。实际上是修正每层造成的错误沿着层向前积累。可以看出asymmetric比symmetric有更低的错误率。
VGG是一个广泛使用的网络模型,是一个深度网络,其被广泛用于物体识别,图像分割,视频分析中。作者在VGG-16上进行了实验,实验结果和CP分解的做了对比,如图:
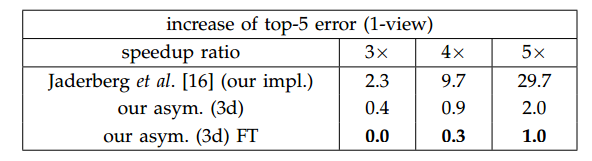
结论
本文介绍了另外一种降维方法,其可以优化深度网络。个人感觉其还是有一定局限性,首先其在网络前向传输优化时,错误率还是会进行积累,这也是仅仅优化了16层VGG的原因,当然这相比CP分解确实加深了。但是类似resnet这样更深的网络,作者并没有报道过。
文章转载自: AI加速