作者:默宸,来源: FPGA技术联盟
所谓普通时序系统(共同时钟系统)就是指驱动端和接收端的同步时钟信号都是由一个系统时钟发生器提供。
No.1:数据传输过程
下图是一个典型的普通时钟系统的示意图,是计算机系统的前端总线的时序结构,即处理器(CPU)和芯片组(Chipset)之间的连接。
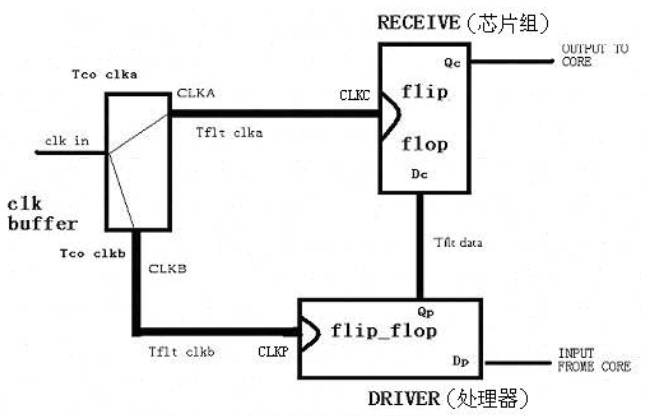
驱动端(处理器)向接收端(芯片组)传送数据,我们可以将整个数据传送的过程分为三个步骤:
step1:核心处理器提供数据;
step2:在第一个系统时钟的上升沿到达时,处理器将数据 Dp 锁存至 Qp 输出;
step3:Qp 沿传输线传送到接收端触发器的 Dc, 在第二个时钟上升沿到达时, 将数据传送到芯片组内部。
No.2:建立时间的重要性
通常,标准普通时钟系统的时钟信号到达各个模块是同步的,也就是说图中的 Tflight clka 和Tflight clkb 延时相同。通过分析可以看出,数据从发送到接收的过程需要连续的两个时钟沿,要使系统能正常工作,就必须在一个时钟周期内让信号从发送端传输到接收端。如果信号传输延时大于一个时钟周期,当接收端的第二个时钟沿触发时,就会造成数据读取错误,因为正确的数据还在传输的过程中,这就是建立时间不足带来的时序问题。
目前普通时序系统的频率无法得到进一步提升的原因就在于此。频率越高,时钟周期越短,允许在传输线上的延时越小,200-300MHz 为普通时序系统的频率极限。
那么,是不是传输延时保持越小就越好呢?当然也不是的,因为它还必须要满足一定的保持时间。在接下来内容里,我们就建立和保持时间来分析一下时序设计需要考虑的一些问题以及正确的系统时序所必须满足的条件。
No.3:时序参数的确定
对于时序问题的分析,首先要清楚地理解一些相关时序参数的具体含义,如 Tco,传播延迟,缓冲延时,最大/小飞行时间,建立时间,保持时间,建立时间裕量,保持时间裕量,时钟偏移、时钟抖动,等等,如果对这些参数的概念理解不深刻,很容易造成时序设计上的失误。
首先要阐明的是 Tco 和缓冲延时(buffer delay)的区别。从定义上来说,Tco 是指时钟触发开始到有效数据输出的器件内部所有延时的总和;而缓冲延时是指信号经过缓冲器达到有效的电压输出所需要的时间。可以看出,Tco 除了包含缓冲延时,还包括逻辑延时。通常,确定 Tco 的方法是在缓冲输出的末端直接相连一个测量负载,最常见的是 50 欧姆的电阻或者 30pF 的电容,然后测量负载上的信号电压达到一定电平的时间,这个电平称为测量电压(Vms),通常是信号高电平的一半。如 Tco 和缓冲延时的确定如下图所示:

传播延迟(propagation delay)
信号从缓冲器出来之后,经过传输线到接收终端,信号在传输线上的传输的延时我们称为传播延迟(propagation delay),它只和信号的传播速度和线长有关。而我们在大多数时序设计里面,最关键的却不是传播延迟,而是飞行时间(Flight Time),包括最大飞行时间(Max Flight Time)和最小飞行时间(Min Flight Time)。飞行时间包含了传播延迟和信号上升沿变化这两部分因素,从下图中可以很容易看出两者的区别。

在较轻的负载(如单负载)情况下,驱动端的上升沿和接收端的信号的上升沿几乎平行,所以这时候平均飞行时间和传播延迟相差不大;但如果在重负载(如多负载)的情况下,接收信号的上升沿明显变缓,这时候平均飞行时间会远远大于信号的传播延迟。这里说的平均飞行时间是指 Buffer波形的 Vms 到接收端波形 Vms 之间的延时,这个参数只能用于时序的估算,准确的时序分析一定要通过仿真测量最大/最小飞行时间来计算。
上面是对信号上升沿的分析,而下降沿同样存在着最大/最小飞行时间的参数,如下图。在时序计算时实际取的最大飞行时间是在上升沿和下降沿中取最长的飞行时间,而最小飞行时间则是取上升和下降沿中最短的飞行时间。

也有时候,人们对信号的最大/最小飞行时间还有其它称呼,比如在 Cadence 软件中,将最大飞行时间称为最终稳定延时(Final Settle Delay),而将最小飞行时间称为最早开关延时(First Switch Delay),如下图。

信号经过传输线到达接收端之后,就涉及到建立时间和保持时间,它们是接收器本身的特性,表征了时钟边沿触发时数据需要在锁存器的输入端持续的时间。通俗地说,时钟信号来的时候,要求数据必须已经存在一段时间,这就是建立时间(Setup Time);而时钟边沿触发之后,数据还必须要继续保持一段时间,以便稳定的读取,这就是保持时间(Hold Time)。如果数据信号在时钟沿触发前后持续的时间均超过建立和保持时间,那么超过量就分别被称为建立时间裕量和保持时间裕量。如下图 ,其中还考虑了时钟误差的因素。

器件的建立和保持时间参数,通常都可以在相应的 DataSheet 查到,对于设计者来说,最大的目的是提高时序的裕量,如此,即使信号完整性上出现小问题,或者外界环境发生一定的变化,系统仍然能正常工作,这就是一个设计优良的系统应该体现出的超强的稳定性。
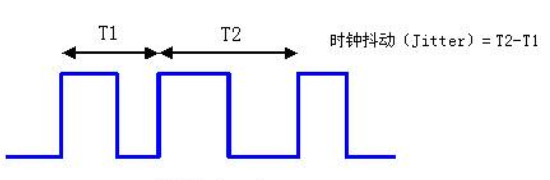
系统时序设计对时钟信号的要求是非常严格的,因为时序计算都是以恒定的时钟信号为基准。但实际中时钟信号往往总是不那么完美,会出现抖动(Jitter)、偏移(Skew)问题。所谓抖动,是指两个时钟周期之间存在的差值,这个误差是在时钟发生器内部产生的,和晶振或者 PLL 内部电路有关,布线对其没有影响,如下图。除此之外,还有由于周期内信号的占空比发生变化而引起的抖动,称之为半周期抖动。总的来说,jitter 可以认为在时钟信号本身在传输过程中的一些偶然和不定的变化之总和。
时钟偏移(skew)是两个相同的系统时钟之间的偏移。它表现的形式是多种多样的,既包含了时钟驱动器的多个输出之间的偏移,也包含了由于 PCB 走线误差造成的接收端和驱动端时钟信号之间的偏移,比如在图 1 中所示,CLKA 和 CLKB 之间的差异,CLKC 和 CLKP 之间的差异均为时钟偏移,这些偏移量在时序计算中需要全部考虑。
除了上面提到的这些概念,还有一点要注意的是,时刻不能忽略信号完整性对时序的影响,比如串扰会影响微带线传播延迟;反射会造成数据信号在逻辑门限附近波动,从而影响最大/最小飞行时间;时钟走线的干扰会造成一定的时钟偏移。有些误差或不确定因素是仿真中无法预见的,设计者只有通过周密的思考和实际经验的积累来逐步提高系统设计的水平。
No.4:时序约束条件
下面来具体讨论一下系统时序需要满足的一些基本条件。我们仍然以图 1 的结构为例,并可以据此画出相应的时序分析示意图。

在上面的时序图中,存在两个时序环,实线的环为建立时间环,虚线的环为保持时间环。可以看到,这两个环都不是闭合的,缺口的大小就代表了时序裕量的多少,因此设计者总希望尽可能增大这个缺口。同时要注意,每个环上的箭头方向是朝着正反两个方向的,因为整个系统时序是以时钟上升沿为基准的,所以我们时序环的起点为系统时钟 clk in 的上升沿,而所有箭头最终指向接收端的控制时钟 CLKC 的边沿。
先来分析建立时间环:
缺口的左边的半个时序环代表了从第一个系统时钟上升沿开始,直到数据传输至接收端的总的延时,我们计为数据延时,以 Tdata tot 表示:
Tdata tot =Tco clkb+Tflt clkb +Tco data +Tflt data
式中:
Tco clkb 是系统时钟信号 CLKB 在时钟驱动器的内部延迟;Tflt clkb 是 CLKB 从时钟驱动器输出后到达发送端(CPU)触发器的飞行时间;
Tco data 是数据在发送端的内部延迟;
Tflt data是数据从发送端输出到接收端的飞行时间。
从 CLKC 时钟边沿的右边半个时序环代表了系统时钟到达接收端的总的沿时,计为时钟延时,以Tclk tot 表示:
Tclk tot =Tcycle +Tco clka +Tflt clka – Tjitter
其中:
Tcycle 是时钟信号周期;
Tco clka 是系统时钟信号 CLKA(第二个上升沿)在时钟驱动器的内部延迟;
Tflt clka 是时钟信号从时钟驱动器输出到达接收端触发器的飞行时间;Tjitter是时钟的抖动误差。因此我们可以根据建立时间裕量的定义,得到:
Tsetup margin = Tclk tot – Tdata tot – Tsetup
将前面的相应等式带入可得:
Tsetup marin = Tcycle + Tco clka + Tflt clka – Tjitter – Tco clkb –Tflt clkb – Tco data – Tflt data – Tsetup
定义时钟驱动器(PLL)的两个时钟输出之间的偏移为 Tclock Skew ,两根 CLOCK 走线之间的时钟偏移为 TPCB Skew ,即:
Tclock Skew = Tco clkb - Tco clka;
TPCB Skew = Tflt clkb - Tflt clka
这样就可以得到建立时间裕量的标准计算公式:
Tsetup marin =Tcycle – TPCB skew –Tclock skew –
Tjitter – Tco data – Tflt data-Tsetup (1.6.1)
再来看保持时间环:
对照上图 ,我们可以同样的进行分析:
Tdata delay = Tco clkb + Tflt clkb + Tco data + Tflt data
Tclock delay = Tco clka + Tflt clka
于是可以得出保持时间裕量的计算公式:
Thold margin = Tdata delay – Tclock dalay – Thold time
即:
Thold margin = Tco data + Tflt data + Tclock skew + Tpcb skew – Thold (1.6.2)
可以看到,式 1.6.2 中不包含时钟抖动 Jitter 的参数。这是因为 Jitter 是指时钟周期间(Cycle to Cycle)的误差,而保持时间的计算和时钟周期无关。
对于任何时钟控制系统,如果要能保证正常工作,就必须使建立时间余量和保持时间裕量都至少大于零,即 Tsetup marin >0;Thold margin >0,将公式 1.6.1 和 1.6.2 分别带入就可以得到普通时钟系统的时序约束条件不等式:
TPCB skew +Tclock skew +Tjitter + Tco data + Tflt data+Tsetup < Tcycle (1.6.3)
Tco data + Tflt data + Tclock skew + Tpcb skew > Thold (1.6.4)
需要注意的是:
数据在发送端的内部延时 Tco data 可以从芯片的 datasheet 查到,这个值是一个范围,在式1.6.3 中取最大值,在式 1.6.4 中取最小值。
数据在传输线上的飞行时间 Tflt data 在实际计算中应该取最大/最小飞行时间参数, 在式 1.6.3中取最大飞行时间,在式 1.6.4 中取最小飞行时间。
时钟的偏移 TPCB skew 和 Tclock skew 也是一个变化的不确定参数,一般为+/-N ps,同样,在建立时间约束条件 1.6.3 中取+Nps,而在保持时间约束条件 1.6.4 中取-Nps。
从上面的分析可以见,对于 PCB 设计工程师来说,保证足够稳定的系统时序最有效的途径就是尽量减小 PCB skew 和信号传输的飞行时间,其它的参数都只和芯片本身的性能有关。实际应用中经常采取的措施就是严格控制时钟和数据的走线长度,调整合理的拓补结构,并尽可能的减少信号完整性带来的影响。然而,即便我们已经考虑的很周全,普通时钟系统的本身的设计瓶颈始终是无法打破的,也就是建立时间的约束, 我们尽可能的减少由 PCB 布线引起的信号延迟之外,器件本身的特性如 Tco、Jitter、TSetup 等等将成为最主要的制约因素,尽管可以通过提高工艺水平和电路设计技术来不断提高数字器件的性能,但效果也仅仅是在一定范围之内提升了系统的主频,在频率超过300MHz 的情况下,我们将不得不放弃使用这种普通时钟系统设计。