作者:默宸,来源: FPGA技术联盟
跳频通信具有良好的抗干扰、抗多径衰落、抗截获等能力和同步迅速等特点,广泛应用于军事、交通、商业等各个领域。其关键技术主要有三点:跳频序列发生器、跳频频率合成器和跳频同步器。频率合成器是跳频系统的心脏,直接影响到跳频信号的稳定性和产生频率的准确度,在跳频频率合成器中,直接数字式频率合成器(Direct Digital Synthesizer :DDS)使用最为广泛。DDS这简单可靠、控制方便,且具有很高的频率分辨率和转换速度,非常适合跳频通信的要求。
01、DDS的基本原理
简单来说,DDS是一种把一系列数字形式的信号通过D/A转换成模拟量形式 的信号合成技术。DDS 有两种基本合成方式:一种是根据正弦函数关系式,按照一定的时间间隔利用计算机进行数字递推关系计算, 求解瞬时正弦函数幅值并实时的送入D/A变换器,从而合成出所需频率的正弦波信号,这种合成方式具有电路简单、 成本低的特点, 并且合成信号的频率分辨率可以做到很高;另一种就是利用硬件电路取代计算机软件运算过程,即利用高速存储器做查询表,通过高速数 / 模转换器产生已经用数字形式存入的正弦波,这是目前使用最广泛的一种直接数字频率合成方法。
根据奈奎斯特取样定理, 对于任意一个频率带宽为 B 的连续信号f(t) 进行抽样, 只要这些取样值的时间间隔小于 1/ 2B (2的B次方分之一),则该表示可包含连续信号f(t)的全部信息的。再对抽样后的信号进行量化, 则原来的模拟信号 f(t) 就变成了一系列的数字序列。将这一系列的量化值通过一定的手段固化在只读存储器中, 每个存储单元的地址即为对应的相位取样地址, 存储单元的内容即为已经量化了的正弦波幅值。这样一个只读存储器就构成了一个与 2π 周期内相位取样相对应的正弦函数功能表。在一定频率的时钟信号的作用下, 通过一个线性的计数时序数列发生器所产生的取样地址对已得到的正弦波形存储器进行循环扫描, 近而周期性的读取存储器中的数据,其输出通过数 /模转换器以及低通滤波器就可以合成一个完整的具有一定频率的正弦波了。
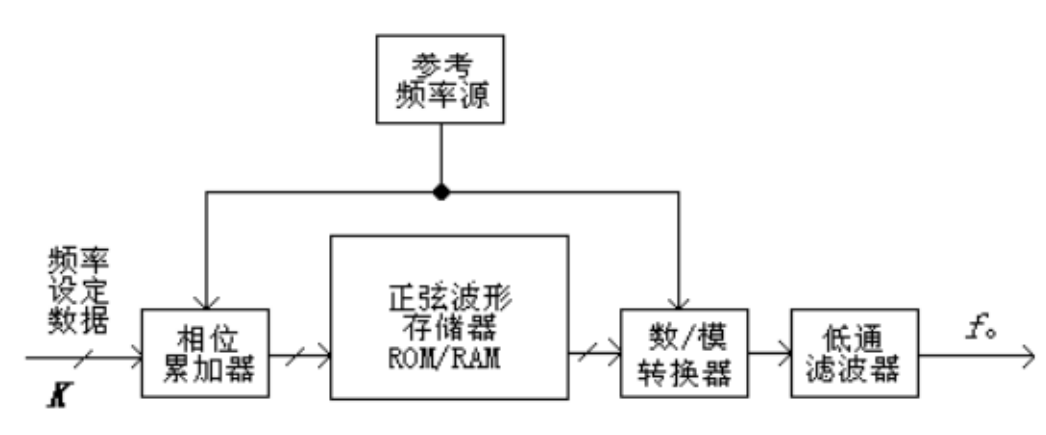
上图中的参考频率源是一个高稳定的晶振,其输出信号用于提供 DDS 中各部件的同步工作。频率控制参数是通过N 位数据锁存器接收的, 把这些数据送到 N 位相位累加器中的加法器数据输入端, 在外部信号未改变合成信号频率指令前, N 位数据锁存器中的数据保持不变。相位累加器由 N 位加法器与 N 位累加寄存器级联构成,如下图:
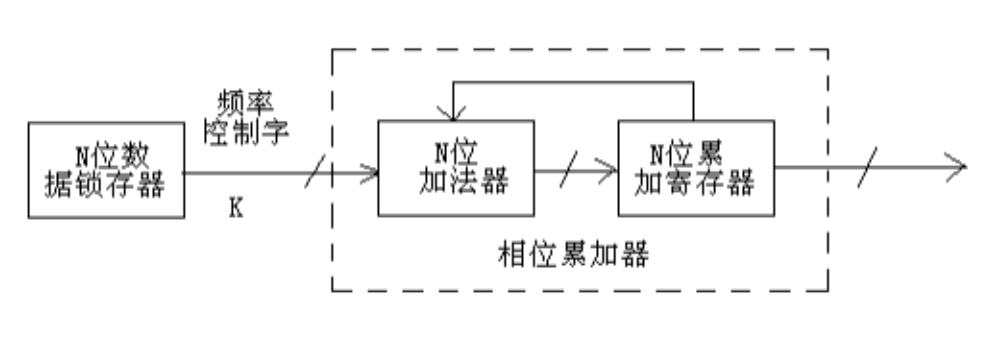
每来一个时钟脉冲, N位加法器就将数据锁存器输出的频率控制数据 K与 N位累加寄存器输出的累加相位相加,相加后的结果送至 N 位累加寄存器的数据输入端。累加寄存器则将加法器在上一个时钟作用后所产生的新相位数据反馈到加法器的输入端,以使加法器在下一个时钟的作用下继续与频率控制数据相加。这样,相位累加器在参考频率时钟的作用下,不断对频率控制数据进行线性相位累加,当累加器累积满量时就会产生一次溢出, 从而完成一次周期性动作, 这个动作就是 DDS 合成信号的一个频率周期, 累加器的溢出频率就是 DDS 输出信号的频率。
对于具有 M 个相位取样的正弦波波形存储器, DDS 输出最低频率即频率控制字设置为 1 时,读出一个周期的信号需要 M 个参考频率时钟周期,相当于输
出一个频率为fmin = fc/M 的正弦波合成信号。若频率控制数据为K,读出一个周期的信号需要 M/K 个参考时钟周期,合成信号的频率为fo= fc*K/M ,这就是 DDS 输出信号的频率关系表达式, DDS 的频率分辨率为△f = fc/M,其中M=2N (2的N次方)。
在直接数字合成器中,正弦函数波形存储器(ROM)的字节数决定了相位量化误差,每个单元内的比特数决定了幅度量化误差。在实际的 DDS 中,利用正弦波的对称性, 360°范围内的幅、 相点可以减少到 90°以内,以降低 ROM的内存容量。由于数 / 模转换器实际上是以固定的时钟速率fc对不同频率的正弦波进行取样合成的,随着输出频率fo的增加,相位取样数量减少,相位量化误差加大,量化噪声和杂波加大,根据取样定理的条件, DDS 理论上输出的最大频率为fmax=fc/ 2,实际工作中最大频率fo max=fc/ 2。
02、基于DDS的跳频信号产生核心模块的设计
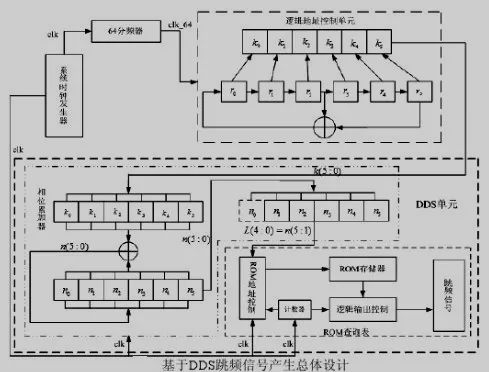
如图所示,整个系统由两个部分组成,逻辑地址控制单元和 DDS 单元。逻辑地址控制单元用来产生不同的频率控制字,改变相位累加器的累加值。DDS 单元依据频率控制字产生相应频率的信号,包括相位累加器和 ROM 查询表。
逻辑地址控制单元
在本设计中,逻辑地址控制单元由一个 6 级移位寄存器和 6 位存储器构成。系统时钟 clk 经过 64 分频后得到时钟 clk_64, 作为逻辑地址控制单元的驱动时钟。当一个时钟 clk_64 上升沿到来时,r(1:5)=r(0:4)。这样移位寄存器中的状态将改变,并存入存储器中,得到频率控制字 k(5:0)。
DDS 单元
DDS 单元为本设计的核心部分,由相位累加器和 ROM 查询表两部分组成。在频率控制字(5:0)的控制下产生相应频率的信号。
① 相位累加器
相位累加器是 DDS 的重要的组成部分。被用来实现相位的累加,并将其累加结果存储。φn 为一等差数列。如果相位累加器的初值为φ0,则经过一个时钟周期后相位累加器值为φ1,即φ1=φ0+k,其中 k 为频率控制字。当经过 n 个时钟周期后φn=φ0+nk。
在本文中基于 FPGA 的相位累加器设计如上图所示。从上图中可以看出,相位累加器由一个数字全加器和一个数字存储器构成。为了提高 DDS 输出频率的分辨率,n要足够大,这样就要求 ROM 中存储大量数据。但是考虑到硬件资源有限,所以在相位累加器中采用了截短处理,既保证了较小的频率分辨率,又节省了硬件资源。
② ROM 查询表
ROM 中存储的数据是数字波形的幅值,在一个系统时钟周期内,相位累加器可输出一个位宽为 L 的序列对其进行寻址,经过低通滤波器后得到所需要的波形。若相位累加器的输出序列的位宽 L=16,ROM 中存储的数据位宽为 M=16,则可以计算出 ROM 的存储量为 2L×M=1048576bits,虽然FPGA 开发芯片上提供了大量的 ROM,可以显著提高输出信号频率精确度和信号幅值准确性,但这样会使成本提高、功耗增大。
考虑到以上问题,在保证输出信号具有良好频率分辨率的前提下,以产生正弦信号为例,考虑到基于 DDS 产生的正弦波具有周期性,因此本设计的 ROM 中存储 1/4 周期正弦波。如上图 所示为存储 1/4 周期正弦波形 ROM 查询表设计。利用正弦信号的对称性,通过改变 ROM 存储器地址及对其输出端控制,得到整周期正弦信号。
03、仿真结果及分析
DDS单元仿真结果及分析
① 仿真参数
现使用 Xilinx ISE 8.11 中 DDS IP Core 进行对比,分析本设计中 DDS 所产生频率的精确度。在同等仿真参数条件下,分别对本设计的 DDS 和 DDS IP Core 进行仿真测试。表 1 中分别给出基于本设计 DDS 和 DDS IP Core 的仿真参数。

② 仿真结果及分析
如下图所示,clk 是系统时钟,new_dds_sine 为在频率控制字 k=16 时基于本设计 DDS 产生的频率为 1.5625MHz(理论值)的正弦波,dds_ip_ core_sine 为基于 DDS IP Core 产生的频率为 1.5625MHz(理论值)的正弦波。

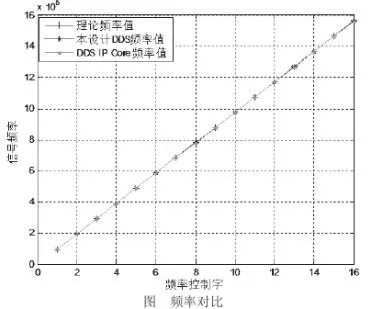
下图 给出在 k 为 1~16 时,本设计 DDS 与 DDS IP Core 所产生信号的频率与理论频率值的对比。从图中可以看出,本设计 DDS 所产生的信号频率与理论频率值比较接近,且本设计 DDS 中 ROM 查询表中存储的点数少,从硬件的角度考虑更加节省资源,能耗更低。
基于 FPGA 跳频信号仿真结果
本设计由系统时钟、分频器、逻辑地址控制单元及 DDS 单元,共四部分组成。跳频信号的产生是通过随机地改变频率控制字来达到改变信号的输出频率,下图 给出了系统工作流程图。
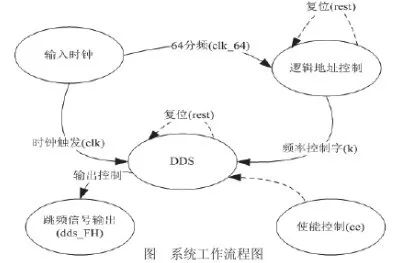
如上图所示,系统时钟 clk 经过 64 分频得到 clk_64。逻辑控制单元由 6 级移位寄存器构成。在每个 clk_64 上升沿到来时,逻辑控制单元将产生一个 6 位的频率控制字(k)。如果DDS 使能信号 ce 为高电平,DDS 将停止工作;如果 ce 为低电平,在 clk 上升沿时 DDS 被触发,在当前状态下 k 的控制下,得到相应地址所对应的信号幅值。如果 k 没有变化,DDS 输出正弦信号的频率没有任何变化,在一个 clk_64 上升沿到来时,k 发生变化,从而使得 DDS 输出的正弦信号的频率发生变化。当复位信号 reset 为高电平时,逻辑地址控制单元和 DDS 单元同时回到初始状态,并保持不变,输出端 dds_FH 输出一直为零。当 reset 变为低电平时,在一个 clk 上升沿时系统开始工作。
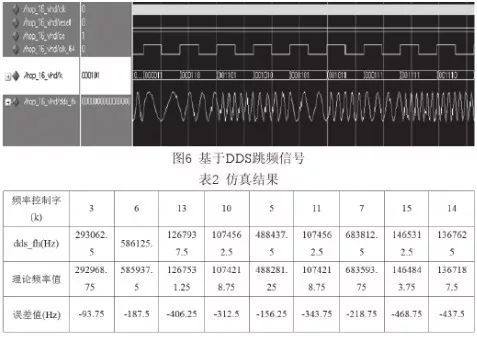
为方便观察仿真结果,本设计采用 ModelSim SE 6.1d 作为仿真波形测试软件。通过以上分析,本设计的 DDS 所产生的频率性能稳定,且跳频信号的误差并不累加。图 6 为基于 DDS 的跳频信号,图 6 给出各个控制信号的仿真结果。表 2 中给出图 6 中不同频率控制字所对应的正弦信号的频率与理论值的对比,可以看出本设计的 DDS 与理论值的误差较小。由于 ROM 中存储的点数较少,更加节省资源。
04、结束语
在 FPGA 硬件平台下设计基于 DDS 的跳频信号产生系统,不仅实现了对大量数据的快速运算,提高了仿真速度,而且可以更灵活地、重复地对系统的参数进行优化配置,便于提高跳频系统的性能。本文所设计的 DDS,结构简单、硬件资源占用率少,且产生频率相对准确。根据对所需跳频信号精确度要求的不同,合理配置参数,协调硬件资源与频率准确之间的矛盾关系,最终实现跳频系统的最优配置。