定点转换不再是 FPGA 或 ASIC 部署的必选项

MATLAB® 和 Simulink® 使用基于浮点的建模来确保算法仿真的高精度计算。转换为定点会降低数学精度，并且转换期间，在数据类型字长和数学精度之间取得适当的平衡会比较困难。对于需要高动态范围或高精度的计算（例如具有反馈回路的设计），定点转换可能会花费数周或数月的工程时间，并且会导致定点字长较大。

从 R2016b 版本开始，您就可以使用 HDL Coder™ 本机浮点库直接从 Simulink 中的单精度浮点数据生成用于 FPGA 或 ASIC 实现的 HDL 代码。

在本文中，我们将以部署到 FPGA 的 IIR 滤波器为例，介绍本机浮点工作流。然后，我们将回顾使用定点的挑战，并比较使用单精度浮点或定点时面积和频率之间的取舍。我们还将展示浮点和定点的组合如何减少实际设计中的转换和实现时间，同时提供更高的精度。您将看到浮点如何在具有高动态范围要求的实际设计中显著缩小面积并提高速度。

本机浮点实现：深入解析

HDL Coder 通过在 FPGA 或 ASIC 资源上仿真基础数学来实现单精度算法（图1）。生成的逻辑将输入的浮点信号解析为符号、指数和尾数，分别为 1、8 和23 位宽的单个整数。然后，生成的 VHDL® 或 Verilog® 逻辑在图 1 所示的情况下执行浮点计算，即通过计算输入符号位产生的符号位、幅值乘法运算，以及添加计算结果所需的指数和相应规范化。逻辑的最后一个阶段将符号、指数和尾数打包回浮点数据类型。

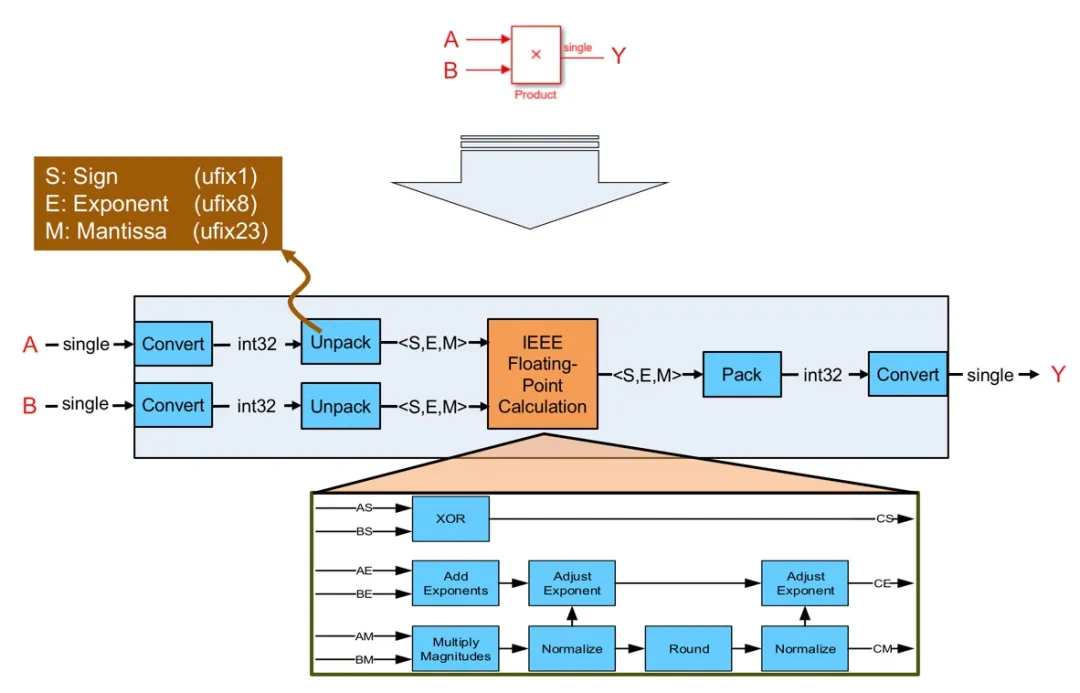
图1. HDL Coder 如何将单精度浮点乘法映射到定点硬件资源

当您在 HDL Workflow Advisor 中选择“本机浮点库”代码生成选项时，HDL Coder 会自动为您的单精度操作执行所有操作。您还可以设置一些选项，以更好地控制如何在硬件中实现浮点运算，例如针对特定的延迟的选项、针对 FPGA 上特定 DSP 逻辑的选项。HDL Coder 还提供了将反常值清零并有效处理 INF 和 NaN 的选项。

用定点转换解决动态范围问题

对于像 1-a/1+a 这样的简单表达式，如果需要在高动态范围内实现，则可以使用单精度自然地进行转换（图2）。

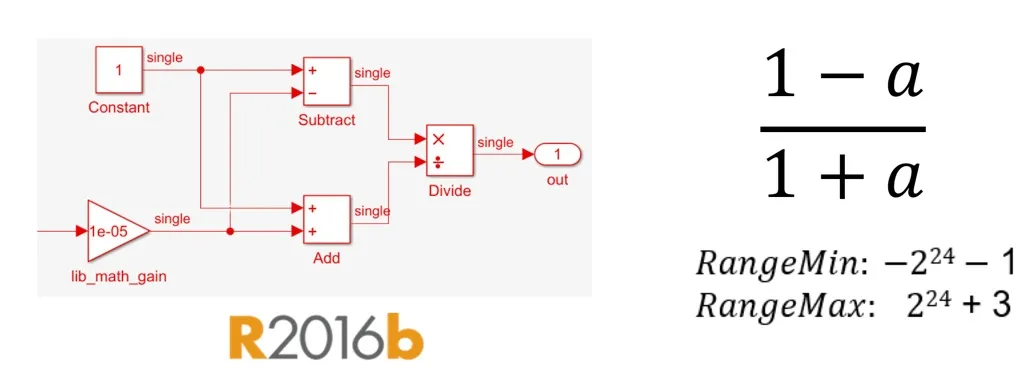
图2. (1-a)/(1+a) 的单精度实现

然而，在定点中实现相同的方程式需要许多步骤和数值方面的考虑（图 3）。例如，必须将除法分解为乘法和倒数，使用牛顿-拉普森或 LUT 等近似方法进行非线性倒数运算，使用不同的数据类型仔细控制位增长，选择合适的分子和分母类型，并对加法器和减法器使用特定的输出类型和累加器类型。

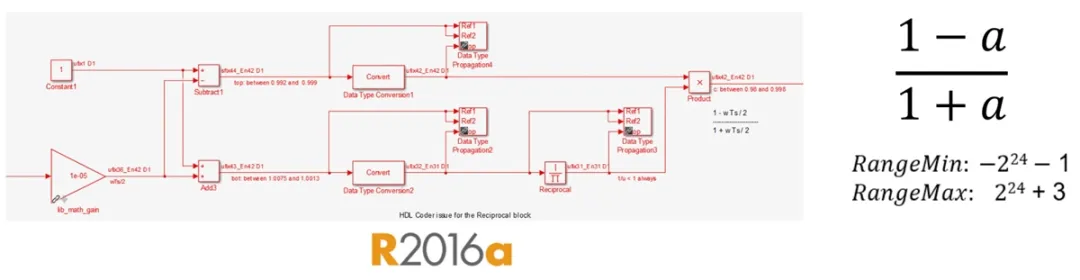
图3. (1-a)/(1+a) 的定点实现

探索 IIR 实现选项

让我们看一个无限脉冲响应(IIR)滤波器的例子。IIR 滤波器需要高动态范围计算和反馈环，这使得它很难收敛到定点量化。图 4a 显示了一个测试环境，比较了具有噪声的正弦波输入的同一个 IIR 滤波器的三个版本。正弦波的振幅为 1，而加性噪声使振幅略有增加。第一个版本的滤波器是双精度的（图 4b）。第二个版本是单精度。第三个版本是定点实现（图 4c）。这种实现导致数据类型的字长最大为 22 位，其中 1 位分配给符号，21 位分配给小数。这种特殊的数据类型留下 0 位来表示整数值，这是很有意义的，因为对于给定的激励，它的值的范围将始终在 -1 和 1 之间。如果设计必须使用不同的输入值，则在定点量化时需要考虑到这一点。

图4. a.具有噪声正弦波输入的 IIR 滤波器的三种实现

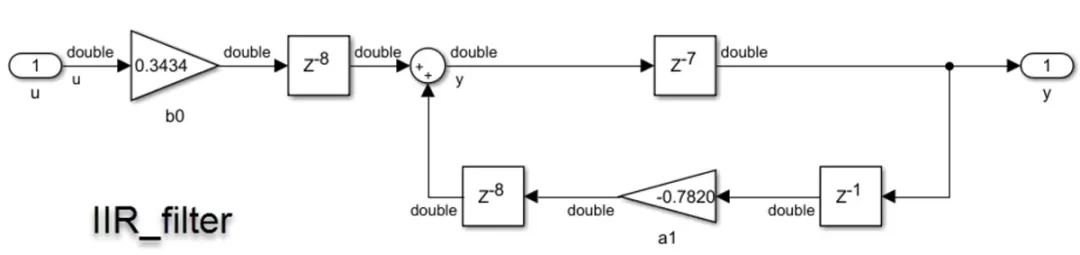
图4b. 以双精度数据类型显示的 IIR_filter 实现

图4c. IIR_filter_fixpt 实现，它使用有符号的 18 位字长定点数据类型，其中 16 位表示小数长度

我们建立了测试环境，以比较单精度和定点滤波器与双精度滤波器的测试结果。在这两种情况下，精度的损失都会产生一定的误差。问题是这个误差是否在我们的应用可接受的公差范围内。

当运行 Fixed-Point Designer™ 进行转换时，我们指定的容错度为 1％。图 5 显示了比较结果。单精度版本的错误约为 10-8，而定点数据类型的错误约为 10-5。这在我们指定的容错范围内。如果您的应用需要更高的精度，则可能需要增加定点字长。

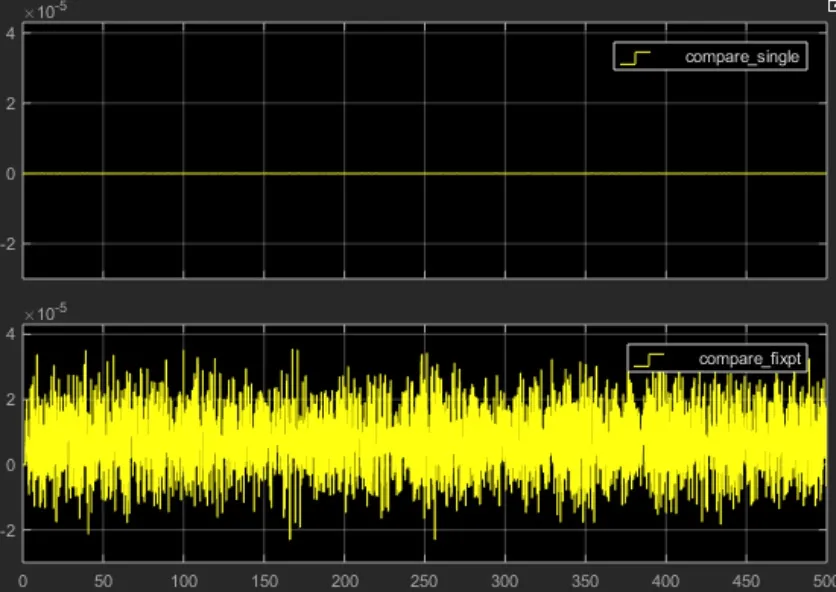
图5.将双精度 IIR 滤波器结果与单精度结果（顶部）和定点结果（底部）进行比较的仿真结果

收敛于这种量化需要硬件设计经验、对可能的系统输入的全面理解、明确的精度要求以及 Fixed-Point Designer 的一些帮助。如果可以帮助您缩减用于生产部署的算法，那么这项工作是值得的。但是，如果您只需要简单地部署到原型硬件上，或者由于精度要求而很难减少资源使用，那该怎么办呢？

这些情况下的解决方法是使用单精度本机浮点。

使用本机浮点简化过程

使用本机浮点有两个好处：

您不必花时间分析所需的最小位数，以保持各种输入数据的足够精度。

单精度浮点运算的动态范围可通过 32 位的固定字长更有效地进行扩展。

现在，设计过程变得更加简单，并且您知道，使用符号、指数和尾数位可以表示很宽的动态数字范围。图 6 中的表使用图 5 中所示的数据类型选择比较了 IIR 滤波器的浮点和定点实现的资源利用率。

图6. IIR 滤波器的定点和浮点实现之间的资源使用率比较

在比较浮点和定点实现的结果时，请记住，浮点计算比简单的定点运算需要更多的操作。在部署到 FPGA 或 ASIC 时，使用单精度将导致更高的物理资源使用率。如果电路面积是一个问题，那么您需要在更高的精度和资源使用率之间进行取舍。您还可以使用浮点和定点的组合来减少面积，同时保留单精度，以在数值密集的计算单元中实现高动态范围。

使用本机浮点管理资源使用情况

本机浮点是为高动态范围应用生成代码的一种简单方法，可用于对 FPGA 编程或部署到 ASIC。但是，如果本机浮点超出了资源预算，有几种方法可以减少资源使用：

使用 HDL Coder 优化。资源共享和其他算法级优化支持本机浮点代码生成。例如，这些优化可以通过时分多路复用和其他共享和流处理技术来共享消耗大量面积的复杂数学运算（例如 exp、atan2），从而达到缩小面积的目的。

在适用的情况下使用定点转换过程。定点转换对于没有高动态范围要求或反馈回路的设计非常简单，而 Fixed-Point Designer 可帮助实现此过程的自动化。在某些类型的设计中，很难在不增加额外位数的情况下实现收敛。在这种情况下，有选择地使用本机浮点是更好的选择。此方法在大多数设计中都使用定点转换，同时允许您在数据路径的高动态范围部分中使用浮点。

在设计中创建浮点和定点“孤岛”。一旦您确定了设计中难以实现收敛的部分，就可以使用数据类型转换模块将输入转换为单精度，然后将操作的输出转换回相应的定点类型来隔离这些部分。图 7 显示了电机控制设计的一部分，其中增益操作和 sincos 操作被隔离为本机浮点区域，并且输出被转换回定点值。

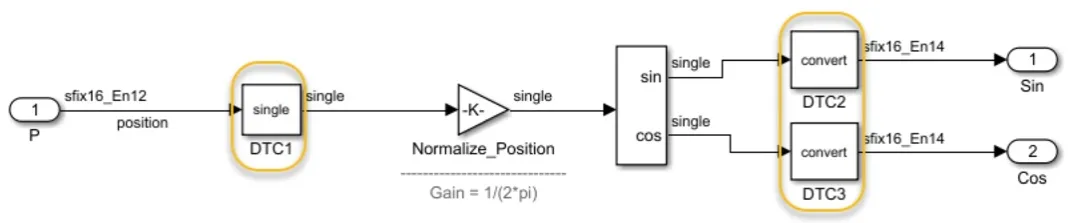
图7.在同一设计中混合使用定点和本机浮点

在设计中选择浮点或定点的快速指南

在以下情况下，对整个设计使用浮点：

您缺乏定点量化的经验。

您的算法混合使用非常大和非常小的数字。

您的设计广泛使用大于 32 位的定点类型。

您的设计包括非线性操作，如 divide、mod、rem、log、exp 和 atan，这些操作很难转换为定点。

您可以灵活地使用更大的面积和延迟（例如，在电机控制或音频处理等较低带宽的应用中）。

在以下情况下，对整个设计使用定点：

您有定点量化方面的经验。

将算法转换为固定点很简单。

您对面积和延迟有严格的要求。

在以下情况下，应混合使用浮点和定点：

您的设计混合使用了控制逻辑和动态范围较大的数据路径。

只有一部分设计难以量化到定点。

对于限定使用的浮点算法，您的面积要求中有足够的余量。

使用本机浮点的实例

如图 8 所示，如果您正在处理动态范围问题并打算使用更长的字长，那么定点实现可能比浮点版本消耗更多的资源。

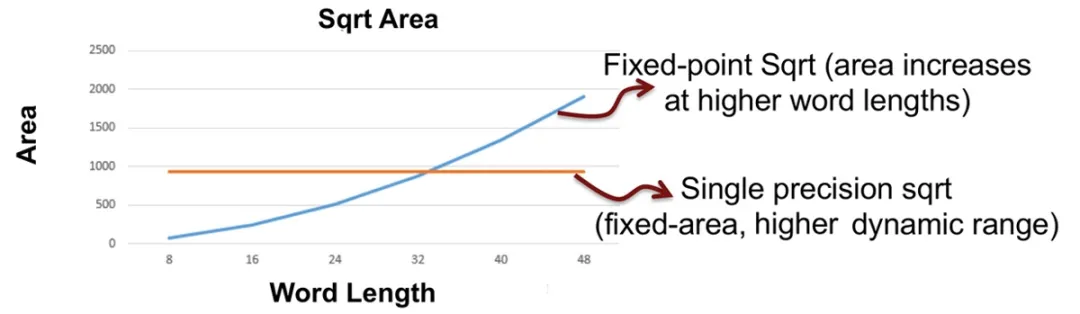
图8. Sqrt 函数资源利用率。在更大的字长下，sqrt 将比单精度实现消耗更多的 FPGA 资源，而后者具有固定的成本

为了解本机浮点在这种情况下是如何发挥作用，请思考一下电动汽车模型的例子（图9）。这是一个包含许多组件的复杂模型，包括电池模型、逆变器、PMSM 和车辆模型。

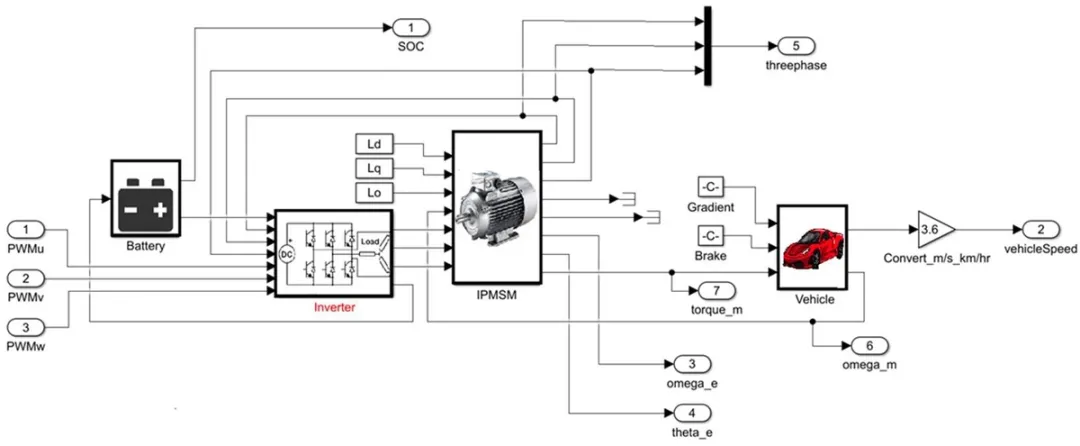
图9.电动汽车模型

图 10 显示了用于实现这些组件的数学方程式。

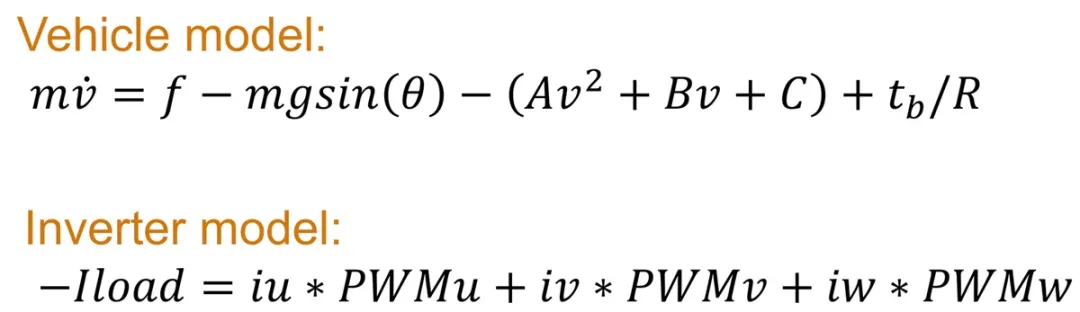
图10.电动汽车模型中使用的数学方程式

由于组件之间的所有反馈回路，通过定点将此模型应用到硬件上可能具有挑战性。在 PMSM 和逆变器之间具有复杂反馈回路的组件系统中，弄清楚如何减少量化误差可能需要几个月的时间。为了减少误差，您必须使用非常大的字长。但是，有了浮点支持，您可以直接将此模型应用在硬件上，而无需将其转换为定点。

如图 11 所示，对于具有反馈回路的算法，浮点是正确的数据类型选择，因为浮点实现使用的面积较小，性能更好，而同一算法的定点版本则需要较大的字长。

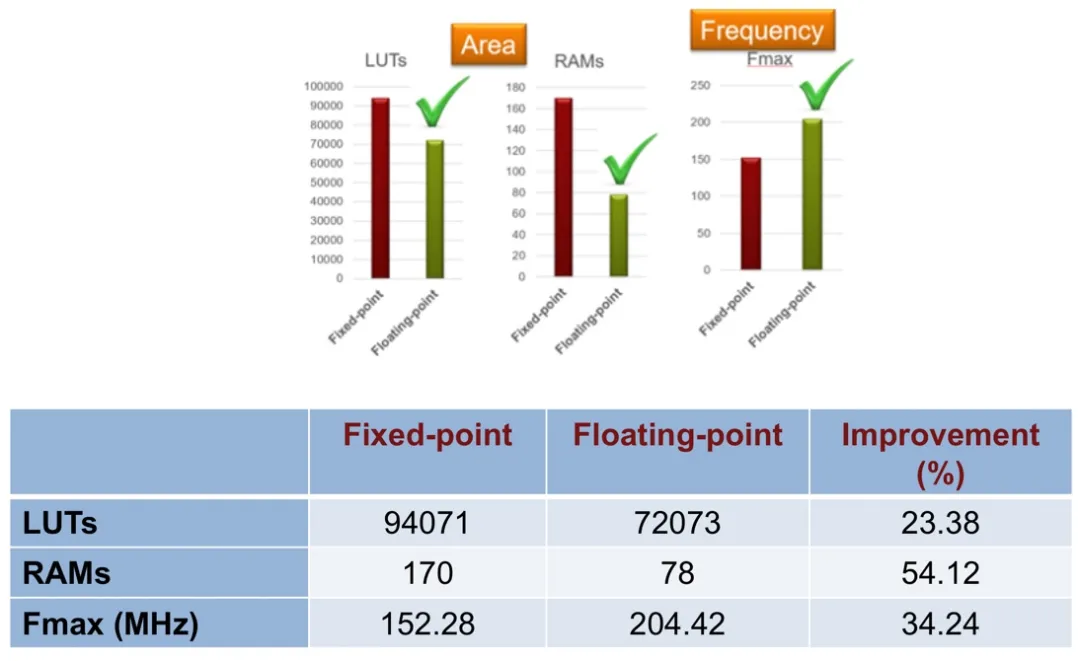
图11.电动汽车模型的定点和浮点实现的比较

结论
习惯上，定点量化一直是使算法满足 FPGA 或 ASIC 硬件要求的最具挑战性的任务之一。本机浮点 HDL 代码生成允许您生成 VHDL 或 Verilog，以便在硬件中实现浮点，而无需进行定点转换。如果您要创建FPGA实现，这种方法可以节省大量时间，并且可以更快地将算法应用到 Xilinx® Zynq® SoC 或 Intel® SoC FPGA。

对于需要两者兼备的设计——既要使用定点的控制逻辑又要使用浮点的高动态范围数据路径，您可以轻松地将两者结合起来。

本文转载自：MATLAB