把波动分解成三角函数是一种将任意周期性函数分解成一系列三角函数的方法。这种方法在信号处理、音频处理、图像处理等领域中得到了广泛的应用。
在波动分解成三角函数的方法中,我们首先需要了解傅里叶级数的概念。傅里叶级数是一种将周期函数分解成一系列正弦和余弦函数的方法。具体来说,对于一个周期为T的函数f(x),它的傅里叶级数可以表示为:
f(x) = a0 + Σ(an*cos(nωx) + bn*sin(nωx))
其中,a0、an、bn是系数,ω=2π/T是角频率,n是正整数。这个式子的意思是,任意一个周期为T的函数都可以表示成一个常数项a0和一系列正弦和余弦函数的线性组合。
在实际应用中,我们通常只需要保留前几项的傅里叶级数,就可以近似地表示原函数了,例如我们认为五次谐波就可以近似的恢复出一个脉冲波。这个近似的程度取决于保留的项数,通常保留的项数越多,近似的程度就越高。
矩形波
矩形波是一种周期为T、幅度在某个时间间隔内保持不变,而在其他时间内归零的波。这个函数可以描述许多实际问题,例如脉冲信号传输和数字通信中的调制技术。激光在光纤中的传输也可以用矩形脉冲来模拟。
举个例子,假设我们有一个周期为2秒的矩形波,幅度为1。在0到1秒的时间段内,波的值为1;在1到2秒的时间段内,波的值为-1。使用傅立叶级数展开这个矩形波,我们会得到一系列奇次频率的正弦函数分量,每个分量都有不同的振幅和相位。这些分量合在一起,形成了原始的矩形波形。


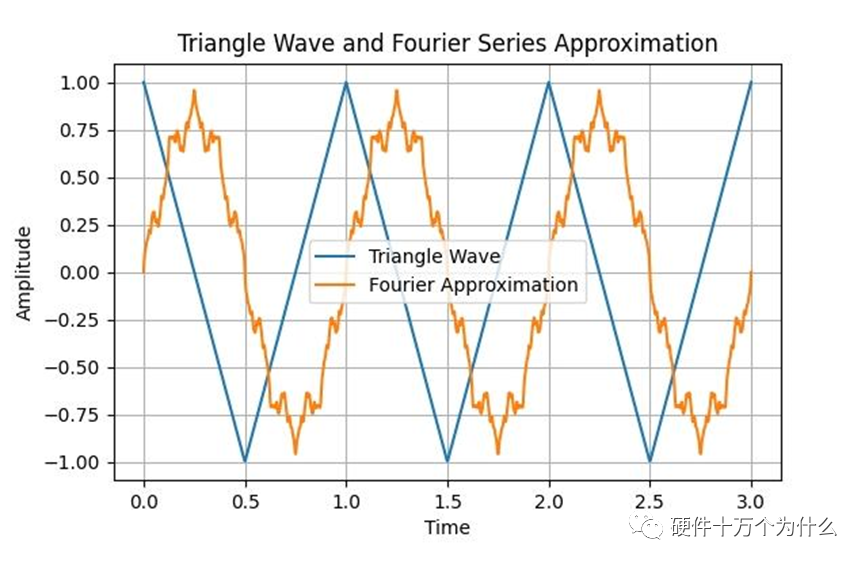
三角波
三角波是一种周期为T、连续上升和下降的波形。它类似于音乐中的提琴声或合成器上的三角波形振荡器。三角波有许多应用,例如在电路中产生频率可控的信号、音乐合成和图像处理。
假设我们有一个周期为1秒的三角波,幅度在0到1秒的时间内从0线性上升到1,然后在1到2秒的时间内线性下降回0。将这个三角波展开为傅立叶级数,我们会发现它包含了无限多的正弦和余弦分量,每个分量都有不同的振幅和相位。通过组合这些分量,我们可以逼近原始的三角波形。
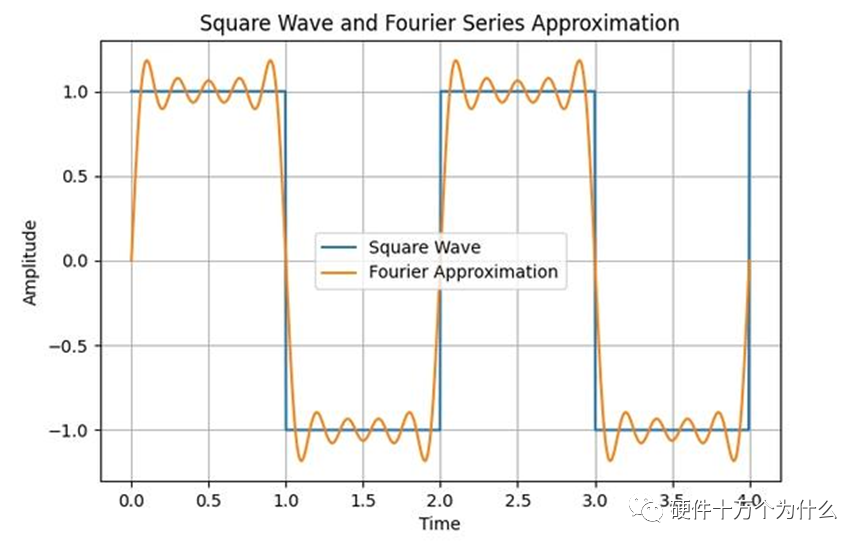
方波
方波是一种周期为T,幅度在某个时间间隔内保持不变,而在其他时间内反转的波形。方波在数字逻辑电路和通信系统中广泛使用,例如时钟信号的生成和数字调制技术。
假设我们有一个周期为2秒的方波,幅度为1。在0到1秒的时间段内,波的值为1;在1到2秒的时间段内,波的值为-1。将这个方波展开为傅立叶级数,我们会看到它由一系列奇次频率的正弦函数分量组成。每个频率分量的振幅逐渐递减,反映了方波形状中的快速变化。
锯齿波

此类物理现象,在电子工程师的日常工作中经常能够看到,我们习以为然的规律需要大量的数学论证。
傅里叶的科学成就主要在于他对热传导问题的研究,以及他为推进这一方面的研究所引入的数学方法。傅里叶对热理论的研究开始于1803 年前后,1807 年底向巴黎科学院呈交了一篇题为《热的传播》的论文,1811年傅里叶又送上了重新修改后的论文《热在固体中的运动理论》,但被当时科学院的审查委员会质疑不严密,而未能及时发表。直到 1822 年出版《热的解析理论》,才将论文的第一部分编入其中。
《热的解析理论》是傅里叶数学和物理贡献的代表作,被认为是数学的经典文献之,对数学和理论物理学的发展都产生了巨大的影响。在书中,一方面,傅里叶按照18世纪的传统方式思考数学,另一方面他所留下的问题又对19 世纪数学的发展产生了巨大的推动作用。这部经典著作将欧拉、伯努利等人在一些特殊情况下应用的三角级数方法发展成内容丰富的一般理论,三角级数后来就以傅里叶的名字命名。
任何函数都可以写成正弦函数之和。(后来证明需要满足狄利克雷条件)
这个想法很简单,但却非常深刻。
这里面包含三个问题:
1、 为什么要分解?
将一个函数做傅里叶变换或者展开为傅里叶级数,可以帮助我们求解线性微分方程,或者从实际意义来说,可以帮助我们分析一个线性系统对外界做出如何响应。
在我们日常工作中经常碰到的:我们把输入信号分解成正弦波,很容易根据滤波器的特性,分析得出输出波形的形态。

2、 为什么是三角函数正弦余弦波,为什么不是其他的波?
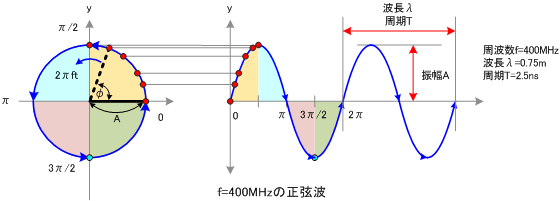
因为三角函数的数学性质好!用正弦函数定义频率,首先是因为正弦函数是最简单的连续有周期性的函数。其次,它在求导算子作用下周期不会变。求导算子的特征函数是e^{ix},看看傅里叶变换的核函数,这说明傅里叶变换在微分方程上做处理很方便,感觉跟数论里的模运算很相似。最后在有限的闭区间上所有连续或者间断点可数的函数构成的空间可以用正弦函数构成的空间逼近,这是空间分解和构成的问题,是信号分析的主要问题。e 的指数函数的导数仍然是e的指数函数。其他函数求导后的变化趋势格式各异,问题变得复杂。
思考了一个问题:我们知道一个时域上是正弦波的电信号,在频谱分析仪上看到是一个单一频谱。那么我们的单一频谱的信号,在波形上为什么是正弦波?而不是一个方波、三角波、半圆波?这是因为我们看到的频谱就是根据傅里叶级数进行分解展开的,我们看到的单一频谱自然就是正弦波。这是一个“循环论证”。。。有这个死循环的想法的原因:我们用频谱分析的时候,就是用正弦波,所以已经习以为常了用三角函数展开了。。。。
3、如何能证明满足条件的任意函数都可以展开成傅里叶级数?
这个证明很复杂,属于泛函分析证明,需要考虑各种情况严格的证明非常繁琐,此处跳过。这个证明在高数书上直接运用了假设,证明过程也是略过的。总之,他可以,数学家已经证明了。
本文转载自:硬件十万个为什么