4. 频谱分析
4.1 傅里叶定理

在时域信号处理的世界里,将信号分解成正弦波的和一直是前进的方向。原因很简单。如果一个正弦波被输入到一个线性系统,那么输出就是一个完全相同频率的正弦波——振幅可能被修改,相位可能被改变,但频率保持不变。考虑到我们总是在DSP中使用线性系统,并且通常假设无线电环境是线性的(或接近线性的),那么通过以正弦波的形式呈现信号或系统的特性意味着我们可以表征频率内容或频谱上的传递函数。这对任何其他基波都不成立。
4.1.1方波的傅里叶级数
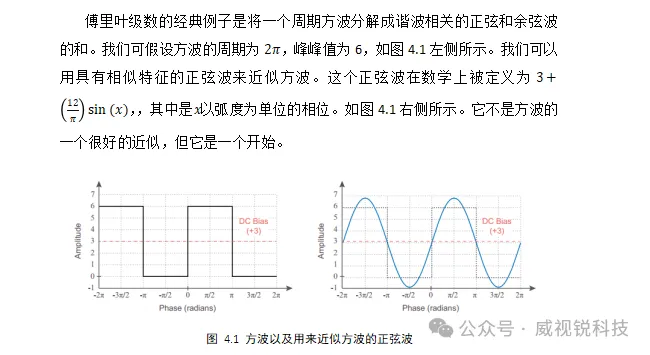
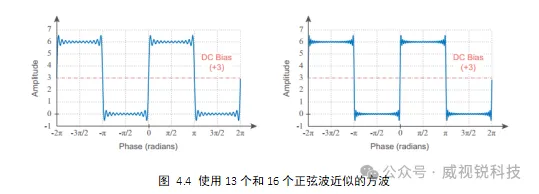
当我们将更多谐波相关的正弦波加在一起时,方波的近似值将得到改善。如图4.4,这些方波近似分别使用13和26个正弦波的总和创建。
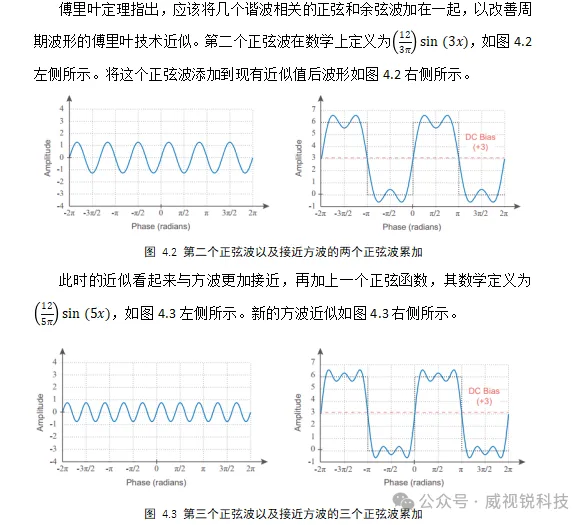
上面例子的要点是探索傅里叶定理的基本原理,我们可以通过将正弦和余弦波相加来表示周期波形。在这个例子中,如果我们把无数个谐波相关的正弦波加在一起,并且有正确的振幅,我们就能来重现方波。我们可以把这个求和写成数学形式。

4.1.2 傅里叶级数系数
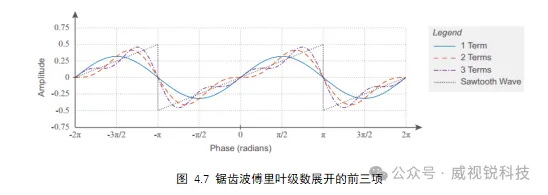
傅里叶级数系数为直流偏置和展开周期函数所需的每个正弦和余弦波提供权重,我们可以通过以下三个方程来计算这些:
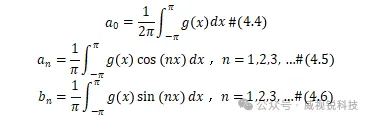
使用上述式子对前述方波的傅里叶级数系数进行计算,可以得到如下式子:
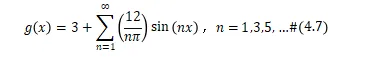
计算(4.8)的前四项并绘制结果进行比较如图4.5所示。方波近似随着累积正弦波数量的增加而改善。
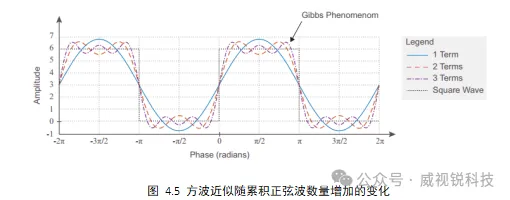
图4.6给出了两个相似的方波,但它们的相位不同。左边的方波是一种特例,它的傅里叶级数只由余弦波组成。右侧的方波表现出相移,与正弦波或余弦波没有相同的相位关系,因此其傅里叶级数展开需要正弦波和余弦波的加权和来正确表示。
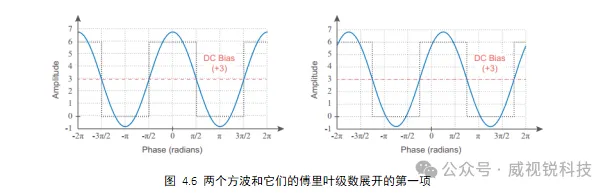
到目前为止,我们只研究了方波的傅里叶级数展开。同样的过程可以用来获得其他周期波形的傅里叶级数展开,如锯齿波。图4.7包含了锯齿波的图和它的傅里叶级数展开的前三项。
4.1.3 时间,频率和谐波
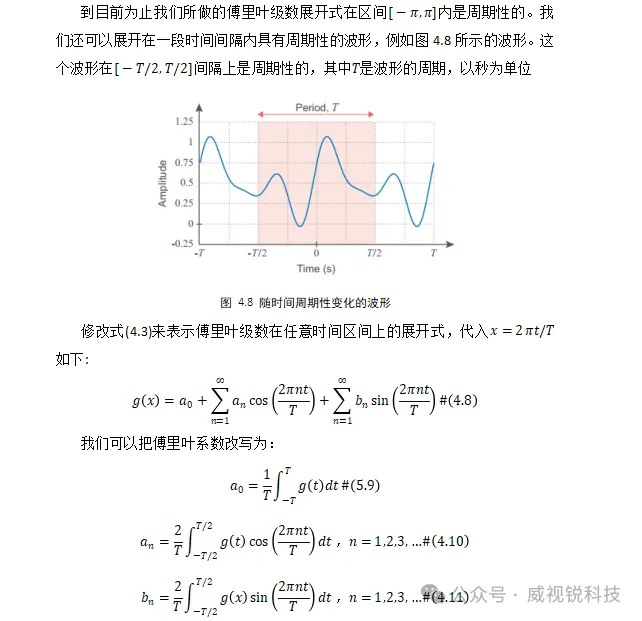
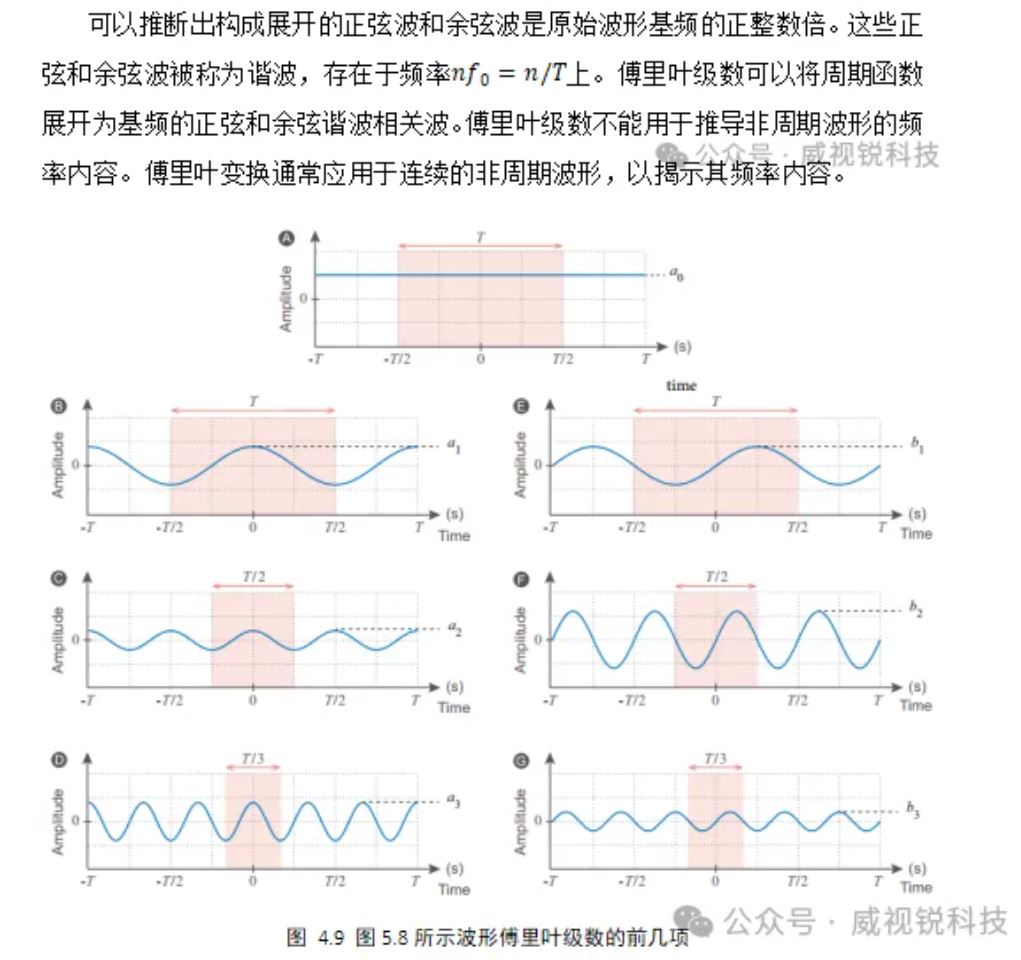
4.1.4 欧拉公式
欧拉公式描述了复指数函数和相关三角函数之间的关系。它可以表示为:
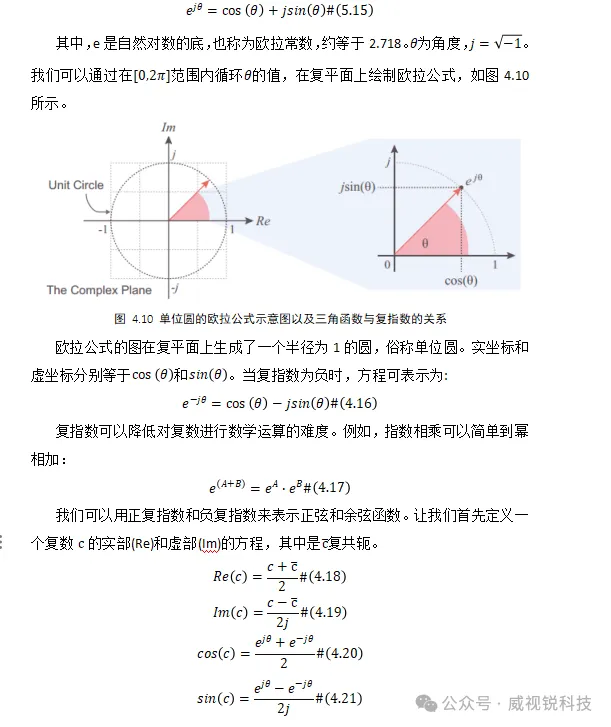
4.1.5 复傅里叶级数
复傅里叶级数展开允许计算复波形的傅里叶级数,即具有实项和虚项的波形。表达式为:

4.1.6 正负频率
注意,式(4.27)中的复傅里叶级数作用于的负值,这意味着我们的傅里叶级数展开将包含基频的负谐波。这些负频率必须用与我们处理正频率相似的方法来处理。讨论正负频率最有效的方法是通过一个使用复傅里叶级数的例子。
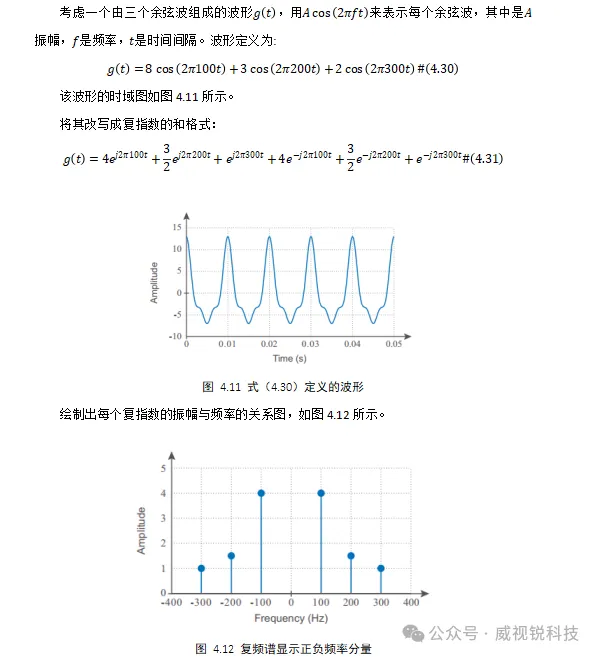
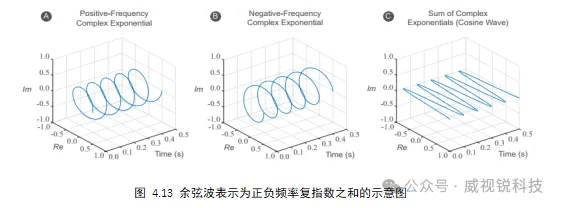
上面给出的图称为复频谱,每个余弦波都有自己相等的正负频率分量。我们可以将余弦波表示为正频率复指数和负频率复指数的和,在4.13中画出该和的示意图。注意,正频率的复指数是一个螺旋,在复平面上沿逆时针方向旋转,而负频率的复指数则沿顺时针方向旋转。
文章来源:威视锐科技