作者:安平博,Xilinx高级工程师;来源:AI加速微信公众号
引言
网络压缩在AI加速中可以说起到“四两拨千斤”的作用,网络参数的减小不仅仅降低了存储和带宽,而且使计算逻辑简单,降低了LUT资源。从本篇开始,我们就一起挖掘一下网络压缩算法的类型,原理,实现,以及效果。写这类算法类文章,一是学习,二是希望能够令更多做FPGA的人,不再将眼光局限于RTL,仿真,调试,关心一下算法,定会发现FPGA的趣味和神通。
网络结构
二值化网络,顾名思义,就是网络参数只有两个数值,这两个数值是+1和-1。在DNN网络中主要是乘和加法运算,如果参数只有两个数值,那么乘法的实现就很简单,仅仅需要符号判断就可以了。比如输入数据A,如果和1乘,不变;和-1乘,变为负数。这用LUT很好实现,还节省了DSP的使用。相对于单精度浮点数,存储减小16倍,带宽也增加16倍。在计算单元数目相同情况下,比浮点运算速率提高了16倍。当然由于乘法和加法使用LUT数目减少,计算单元也会成倍增长,总的下来计算速率将大幅度提高。
网络训练中使用的都是浮点类型参数,这样做是为了保证训练的精度。那么这些浮点类型的参数如何量化的只有两个数值呢?论文中提出了两种方法,第一种是粗暴型,直接根据权重参数的正负,强行分出1和-1。即:

这里wb是二值参数,w是实际权重参数。量化可以看做在原来数据基础上增加了噪声,导致数据间最短距离变大。比如原来数据的分辨率为R0,如果增加一个高斯噪声s,那么其分辨率就增大了。这样在DNN中矩阵乘法中也引入了噪声,为:

数据分辨率的降低导致了有效信息的损失,但是在大量权重情形下,平均下来可以补偿一定的信息损失,即如果有:
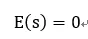
那么在权重无穷多时,有:

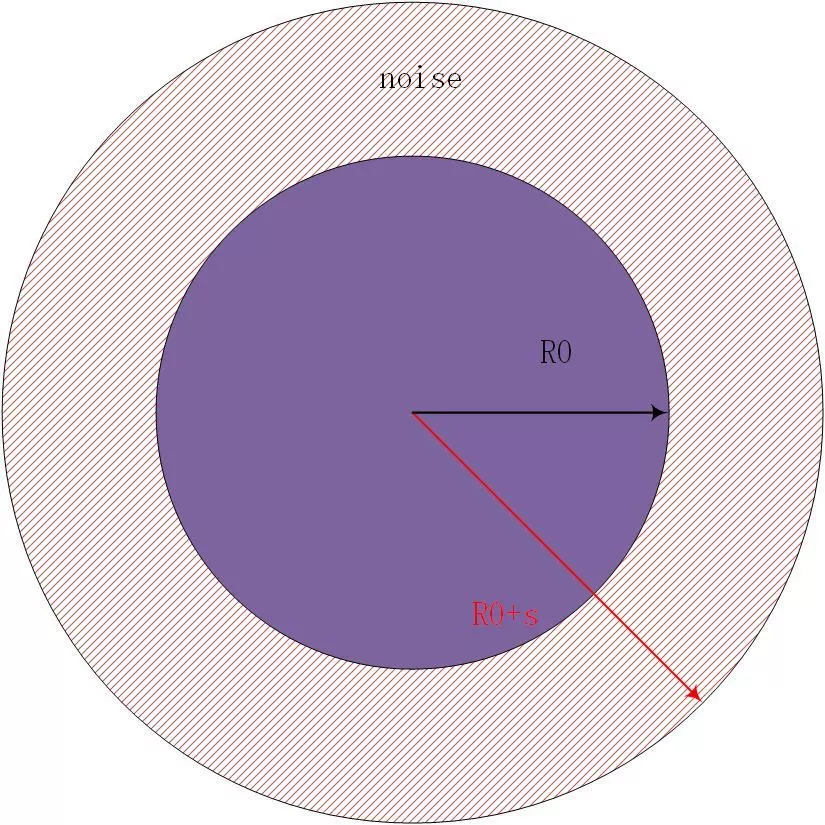
图1.1 数据增加了噪声,导致数据分辨率降低
另外一种是随机型,即以一定概率来选择1和-1,论文中采用如下公式:
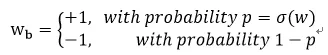
其中“hard sigmoid”函数为:
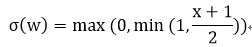
这实际上是对sigmoid函数进行了线性化,这样做的目的可以减少计算量。因为线性计算只有一个乘法和加法,而sigmoid函数有指数计算。使用随机量化更能均衡化量化引入的噪声,消除噪声造成的信息损失。粗暴型量化可能因为权重参数分布不同而发生较大的“不平衡”,比如负数权重较多,那么导致-1远远多于+1,这样就会出现权重偏移在负方向多一些。如果使用随机概率模型,即使负数权重多,也会有一定概率出现+1,弥补了+1较少的情况。
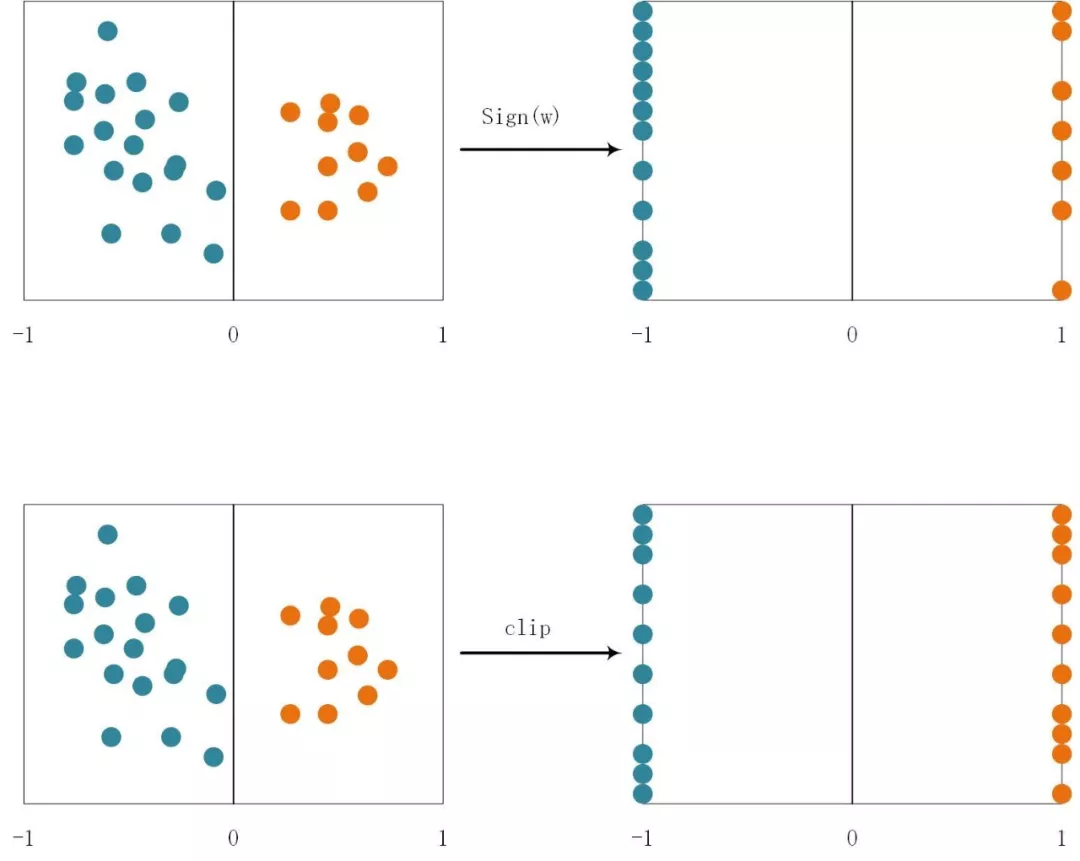
图1.2 粗暴型和随机型量化:随机型量化的分布更加均匀
训练过程
训练过程主要包括三个部分:
1) 前向传播:给定输入数据,一层一层的计算,前一层激活函数的结果作为下一层的输入;
2) 反向传播:计算每一层代价函数的梯度,从最后一层开始计算,反向计算前一层,一直到计算出第一层的梯度值;
3) 更新参数:根据计算出来的梯度和前一时刻的参数,计算出下一时刻的参数。
计算过程可以用图2.1表示:
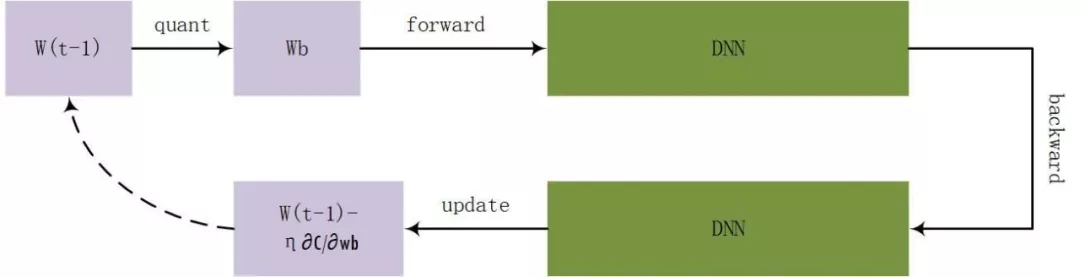
图2.1 训练过程

图2.2 训练算法
每次量化发生在计算出浮点参数之后,然后在进行前向计算,得到代价函数,进行反向计算代价函数梯度,接着利用前一刻参数计算出下一刻数据,不断迭代直到收敛。
结果
论文在三个数据集上进行了测试:MNIST,CIFAR-10,SVHN。
MNIST有6万张内容为0-9数字的训练图片,以及1万张用于测试的28x28大小的灰度图片。论文研究了两种量化方式下训练时间,以及测试出错率。从中看出随机量化出错率更低,更适合用于二值量化。
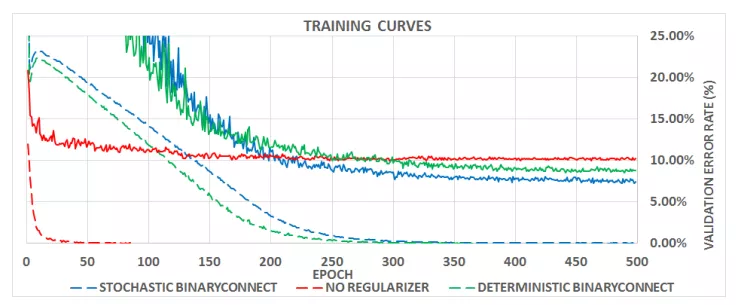
图3.1 不同量化方式下的训练时间以及测试错误率:点线表示训练误差,连续线表示测试错误率
CIFAR-10图片内容比MNIST复杂一些,包含了各种动物。有5万张训练图片和1万张32x32大小的测试图片。
SVHN也是0-9数字图片,含有604K张训练图片和26K的32x32大小的测试图片。以上三种数据集下使用二值网络的结果如下图:

图3.2 三种数据集结果(错误率)比较
从中看出二值网络错误率几乎和其他网络模型差不多,但是其大大压缩了网络模型。
结论
二值化网络中参数只用两个数值表示,实际上仅仅考虑了权重的符号作用。在三种小型简单的数据集上表现良好。
文献
1 Matthieu Courbariaux, Y.B., Binary Connect Training Deep Neural Networks with binary weights during propagations. ArXiv preprint, 2016.
文章转载自:AI加速