本文转载自:CSDN博客
进制是什么?
进制是人为设计的一套带进制计数方法,比如日常使用的十进制,就是0-9这10个数字,每逢十就会向高位进一。因为人类只有十根手指,所以天生地就会想到使用十进制--数到10发现手指头不够用了,就只能进位了。
你想买的某块显卡价格是 ¥2875,那你大概率会把这个价格读作:二千 八百 七十 五 ,而不是简单的:二 八 七 五 。这说明不同位置的数字都代表着不同的含义--由于进制所产生的。如果没有进制的出现,那你今天可能要用某个奇怪的汉字来描述“2875”这个数字(不过没有进制大概率也不会有显卡)了。
当然也有不带进制的计数方法。比如史前人类所用的结绳记事法----每过一天,就在绳子上打一个结,通过数绳结的个数就可以知道天数。

又比如小时候选班长唱票用的写“正”字计数法,通过统计“正”字个数就知道谁能当班长。

为什么计算机使用2进制?
二进制是逢二进一,这意味着在二进制系统中只会有二个数--当然现在我们知道是“0”和“1”,但是为什么?为什么不是“1”和“2”?又或者其他?
“0”和“1”可以直观地理解成“没有”和“有”,当然你也可以用其他数字来表示,只是没有这么直观而已。
“没有”和“有”是自然界最基本的两种状态,比如“灯开了和灯没开”、“吃了和没吃”、“睡了和没睡”······
经常有人说“你是二极管吗?”----意思这人只会单向思考,跟二极管只会单向导通一样。要么就是“通(有)”,要么就是“断(没有)”。
计算机在硬件上可以简单地看做是由晶体管等数字电子电路所构成的。数字电路的一个特点就是它只有两个基本的状态:“通”和“断”,这无疑与二进制完美契合。

什么是原码?
你的Windows操作系统可能是64位的,又或者是32位的?那么这2个数字意味着什么?
64 和32指得是CPU的字长,即CPU每次能处理64位或者32位的二进制数据。后文为了简化理解,我一概将CPU字长假定为8位,所以你现在只能使用8位Windows了。
对于一个数,计算机需要使用一定的编码方式进行存储和处理,而原码就是其中一种编码方式。通俗来讲,原码可以视为一个数的2进制表示形式。比如十进制数11转化成二进制数就是:11--0000_1011,其他类推。在8位字长下,能表示的2进制数分别是0000_0000--0000_0001--0000_0010--·····--1111_1111,即十进制的0-255。
这种表示方法有个问题就是无法表示负数。严格来说,在十进制中要表示正数应该在前加正号,比如数字 正五 = +5,而负数表示则应加上相应的负号,如数字 负五 = -5。正负号就是我们用来区分数字正负的一种方式。现在糟了,人类可以分“正负”,但是计算机只有“0”和“1”啊,并没有“正”和“负”,那么计算机要怎么表示负数?
把8位字长的某一位(通常可以看做是最高位)拿出来,用“0”和“1”分别来对应“正”和“负”不就完事了吗?比如:
负五:-5 = 1000_0101
负三:-3 = 1000_0011
这解决了负数的表示问题,却引入了新的问题:0000_0000和1000_0000居然分别表示+0和-0?嗯?这也太反数学了吧?我们都知道0既不是正数也不是负数,那这会咋有一正一负两个0了?
问题还会出现在计算上:
正数 + 正数:理论上(+1) +(+1) = +2 ;实际上0000_0001 +0000_0001 = 0000_0010,即+2--结果无误。
负数 + 负数:理论上(-1) +(-1) = -2;实际上 1000_0001 + 1000_0001 = 0000 0010,即+2--结果错误。
正数 + 负数:理论上(+1) +(-1) = 0;实际上 0000_0001 + 1000_0001 = 1000 0010,即-2--结果错误。
可见,只要计算中出现了负数,直接采用原码计算结果就已经不可靠了。
而我们人类做这些计算的思维是:
正数 + 正数:1、直接做加法。2、最终符号为正号。
负数 + 负数:1、两个数的绝对值做加法;2、最终符号为负号。
正数 + 负数:1、判断两个数的绝对值大小;2、用较大的绝对值 - 较小的绝对值(减法运算);3、最终符号取绝对值较大数的符号。
在上面的计算中,我们把 正数减正数 的减法转换成了 正数加负数 的加法,这样做的原因是可以和计算机内部的加法电路统一起来。
计算器内部当然可以实现减法电路,但是为了减法而单独构建电路无疑会增加成本和系统复杂性,所以人们尽可能地想办法把加法和减法用一套电路给实现。此外,最高位的符号位也参与了计算,同样是为了统一实现电路。
什么是补码?
教科书上一般就是说:负数的补码是其反码+1。这只告诉了我们怎么求补码,但没告诉我们补码到底是个什么东西?至于反码,我暂时觉得没必要讨论。不如先来聊聊钟表。
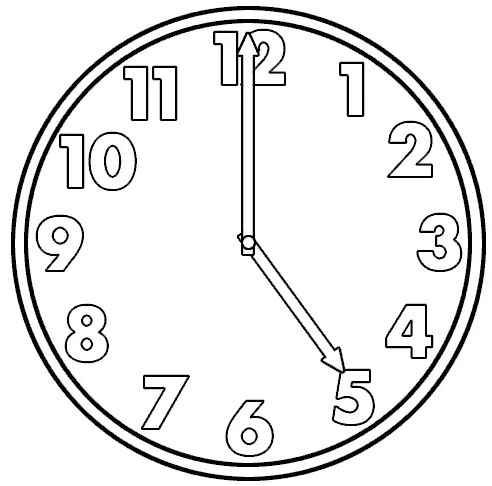
不知道你们有没有注意过,为什么几乎所有的钟表都是12这个刻度却不用0这个刻度?明明这俩不就是同一个时间吗?钟表几乎都是采用的12小时制,而1天却有24个小时,所以尽管上面的时间显示是5点,但是我却无法知道具体时间到底是上午还是下午。
假设现在我们需要把这个钟表从5:00(再假设这是上午时间)调整到2:00,应该怎么做呢?方法有两种:
(1)逆时针调表法

逆时针方向将时针从 5 调整 到 2,这样时针走过的小时数是 5点到 2点共3个小时。
(2)顺时针调表法

顺时针方向将时针从 5 调整 到 2,这样时针走过的小时数是 5点到12点为7个小时,加上12点(即0点)到2点的2个小时,共7+2=9个小时。
两种方法都可以达到同样的目的,而且这两种方法时针所走过的时间数刚好是一个钟表的最大刻度--12小时(3+9),这是巧合吗?
某种程度上,逆时针调表可以看做是一个减法,即 5 - 3 =2。而顺时针调表则可以看做是一个加法,即5 + 9 = 12 + 2 = 14,而14 就是24小时制中的下午2点。这说明在12小时进制中,14和2的意义是一样的!!!同时还说明,减法可以通过某种形式转换成加法!!!
减法转换成加法是有限制条件的,即这个进制系统是有明确容量的。假设某个钟表是无穷大,也就是说它能表示的时间刻度是无限,那么你就无法同时通过顺时针与逆时针的调表方式来实现同一个效果了。
钟表可以看做是一个简单的12进制系统,它所采用的数字我这里借助一下16进制的数字,即0-9,A(十进制数字10)和B(十进制数字11),那么十进制数字14在十二进制应该是12--左边的1表示1*12=12个小时,而右边的2则表示2*1 = 2个小时,加起来就是12 + 2 = 14小时。
现在回到顺时针调表的问题,假设顺时针转到2:00后,再顺时钟转了1圈,效果是不是一样的?毫无疑问,此时仍是钟表刻度2,但在数学意义上此时已经是 5 + 9 + 12 = 26了,26用12进制来表示就是22--左边的2表示2 * 12 = 24个小时,而右边的2则表示2*1 = 2个小时,加起来就是24 + 2 = 26小时。此外,可以类推到转两圈的10进制的38小时 = 12进制的32,转三圈的10进制的50小时 = 12进制的42······
12进制的02--12--22--32--42这几个数字在最低位上都是2,而最高位每加1则意味着钟表多转了1圈。但是钟表它会告诉你它转了几圈吗?不会,所以12进制的最高位这个数字对于钟表的使用是没有实际意义的,它相当于被舍弃了。
现在我们知道在有限容量范围内可以用加法来实现减法,所以回头来看计算机的2进制减法。我们仍然实现从5到2这个过程,即十进制的 5 - 3 = 2,又或者说 5 + 9 =14 =12 + 2。
十二进制的 5 - 3 = 2,在二进制内是 0000_0101 + 1000_0011 = 1000 1000,结果为 -8,显然不行;十二进制的 5 + 9 = 14 = 12 + 2 = 2(舍去最高位表示的12),在二进制是0000_0101 + 0000_1001 = 0000_1110,结果为14,同样不行。
咦?奇怪,不是减法转加法吗,怎么结果还是不行?
问题出现在加数9上,在表盘中加9,是因为减3所走的刻度和加9所走的刻度刚好是一个钟表一圈的刻度(即容量)。走上一整圈,钟表时间向虚拟的高位进位后,才会发生虚拟的高位被舍弃现象!
现在我们做减法的不是12容量的钟表了,而是8位字长的二进制数,那么容量是多少?很简单,2^8 = 256(即0-255这256个数字)。所以,此时就不应该加上9(12 + |-3| = 9)了,而是应该加上253(256 + |-3| = 253)了,即二进制的 1111_1101。所以5-3 可以转换为 5 +(256-3)= 5 + 253 = 258 = 256 + 2,即二进制的1_0000_0010,这个结果有9位,但是我们的CPU只有8位,所以最高位也会被舍去,即最终结果为2进制的0000_0010----10进制的数字2,结果正确!
所以补码是为了将减法转化成加法的一种人为规定的对负数的编码形式。
补码的英文名是 Two's complement ,粗暴点翻译就是 2的补集。这一点可以从其推导方式看出来,负数的补码 = 容量 - 负数的绝对值。比如8位字长CPU能表示的最大容量为 2^8 = 256,所以-1的补码是256 - |-1| = 255,即1111_1111;-15的补码是 256 - |-15| = 241,即1111_0001,其他类推······
什么是反码?
正数的反码一般认为是它自身,当然也有人说反码对正数没有实际使用意义,正数就不存在反码(我对此持赞同意见)。
负数的反码实现有两种说法:
说法一:负数的反码是将负数原码中除符号位以外的所有位按位取反,例如十进制数-42的二进制原码是1010_1010,所以反码是 1101_0101。
说法二:负数的反码是将其绝对值对应正数的原码的所有位按位取反,例如十进制数-42的绝对值为42,其二进制源码是0010_1010,所以反码是 1101_0101。(我个人比较赞同这种说法)
不论说法一和说法二,结果都是一样的。
任何一对绝对值相同的正数和负数,其正数原码与负数的反码相加,其值都是全1。例如+42原码是 0010_1010,-42的反码是1101_0101,加起来就是1111_1111。很显然,出现这种情况的结果是因为,这两个数的每一位都是相反的,我想这可能也是反码这个中文译名的由来。

反码的英文名叫Ones' complement,粗暴点翻译就是 1们的补集 或者 多个1的补集。反码本质上是在求一个正数的算术负数,也就是说,将数字的所有位取反产生的结果与从 0 中减去该值的结果相同。
在上节中,我们说到,负数的补码 =容量(模) - 负数的绝对值 ----式①。
好家伙,前面说了半天补码的出现就是为了把减法转换成加法来简化电路,结果这里又需要通过减法来求一个数的补码,搁这套娃呢?别担心,这时反码就发挥作用了。
8位字长下,任何一个负数与其反码相加结果均为全1,即 正数原码 + 负数反码 = 1111_1111。8位字长下容量是1_0000_0000,即2^8 = 256,而1_0000_0000 = 0_1111_1111 + 0_0000_0001。也即 容量(模) = 1111_1111 + 1 = 正数原码 + 负数反码 + 1 ---式② 。
结合①②式:
负数的补码 =容量(模) - 负数的绝对值 ----①
容量(模)= 正数原码 + 负数反码 + 1 ---②
所以 负数的补码 = 正数原码 + 负数反码 + 1 - 负数的绝对值 = 正数原码 + 负数反码 + 1 - 正数原码 = 负数反码 + 1,这也就是我们常说的:负数的补码等于取反 + 1 。这样就也把对负数求补码的运算在电路上给转换成了 按位取反 和 加法(+1) 运算了,这是数字电路很容易实现的形式。
事实上,根据取反+1来求一个负数的补码只是一种简便方法,而并不是一般定义。一般定义仍是 负数补码= 模(容量) - 负数对应的绝对值。接下来我们就会发现一个数无法使用取反+1的方法来求得。
-128的补码为什么是1000_0000?
在8位字长中,通过 原码 = 补码取反 + 1 和 补码 = 原码取反+1的方法可以求得大多数负数的原码和补码,只有一个例外,即-128的补码是1000_0000。因为-128在8位字长下是不存在原码和反码的。
原码的表示范围是-127~127,其中包括+0 = 0000_0000,-0 =1000_0000。反码的表示范围也是-127~127,其中包括+0 = 0000_0000,-0 =1111_1111。
而在补码中却没有+0和-0,而只有一个0,即0000_0000,这样在补码中多出来的一个数会表示什么?答案显然是-128。
从补码的定义看,-128的补码 = 模 - |-128| = 256 -128 = 128,即二进制的 1000_0000。
从数学连续性上看,正数是:
0000_0000 = 0;
0000_0001 = 1;
0000_0010 = 2;
~~~~~~~~~~
0111_1110 = 126;
0111_1111 = 127;
而负数则是:
1111_1111 = -1;
1111_1110 = -2;
1111_1101 = -3;
~~~~~~~~~~
1000_0001 = -127;
1000_0000 = -128;
所以-128的补码天然就是1000_0000,而非人为定义。同时,在8位字长下,-128是不存在原码和反码的,自然也就谈不上使用 取反+1 的方法了。