1、什么是Setup 和Holdup时间?
答:Setup/hold time 是测试芯片对输入信号和时钟信号之间的时间要求。
建立时间是指触发器的时钟信号上升沿到来以前,数据稳定不变的时间。输入信号应提前时钟上升沿(如上升沿有效)T时间到达芯片,这个T就是建立时间-Setup time。如不满足setup time,这个数据就不能被这一时钟打入触发器,只有在下一个时钟上升沿,数据才能被打入触发器。
保持时间是指触发器的时钟信号上升沿到来以后,数据稳定不变的时间。如果holdtime不够,数据同样不能被打入触发器。
2、什么是竞争与冒险现象?解决办法?
答:在组合逻辑中,由于门的输入信号通路中经过了不同的延时,导致到达该门的时间不一致叫竞争。产生毛刺叫冒险。如果布尔式中有相反的信号则可能产生竞争和冒险现象。
解决方法:一是添加布尔式的消去项,二是在芯片外部加电容。三加选通信号。 用D触发器,格雷码计数器,同步电路等优秀的设计方案可以消除。
3、如何解决亚稳态? Metastability
答:亚稳态是指触发器无法在某个规定时间段内达到一个可确认的状态。当一个触发器进入亚稳态时,既无法预测该单元的输出电平,也无法预测何时输出才能稳定在某个正确的电平上。在这个稳定期间,触发器输出一些中间级电平,或者可能处于振荡状态,并且这种无用的输出电平可以沿信号通道上的各个触发器级联式传播下去。
解决方法:
① 降低系统时钟频率
② 用反应更快的Flip-Flop
③ 引入同步机制,防止亚稳态传播
④ 改善时钟质量,用边沿变化快速的时钟信号
关键是器件使用比较好的工艺和时钟周期的裕量要大。
4、说说静态、动态时序模拟的优缺点
静态时序分析是采用穷尽分析方法来提取出整个电路存在的所有时序路径,计算信号在这些路径上的传播延时,检查信号的建立和保持时间是否满足时序要求,通过对最大路径延时和最小路径延时的分析,找出违背时序约束的错误。它不需要输入向量就能穷尽所有的路径,且运行速度很快、占用内存较少,不仅可以对芯片设计进行全面的时序功能检查,而且还可利用时序分析的结果来优化设计,因此静态时序分析已经越来越多地被用到数字集成电路设计的验证中。
动态时序模拟就是通常的仿真,因为不可能产生完备的测试向量,覆盖门级网表中的每一条路径。因此在动态时序分析中,无法暴露一些路径上可能存在的时序问题;
静态时序分析缺点:
1、无法识别伪路径
2、不适合异步电路
3、不能验证功能
5、用VERILOG写一段代码,实现消除一个glitch。
滤掉小于1个周期glitch的原理图如下:
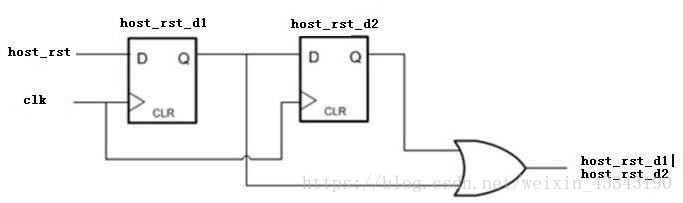
verilog代码实现如下:
module digital_filter_(clk_in,rst,host_rst,host_rst_filter);
input clk_in;
input rst;
input host_rst;
output host_rst_filter;
reg host_rst_d1;
reg host_rst_d2;
always@(posedge clk_in or negedge rst)
begin
if(~rst)
begin
host_rst_d1 <= 1'b1;
host_rst_d2 <= 1'b1;
end
else
begin
host_rst_d1 <= host_rst;
host_rst_d2 <= host_rst_d1;
end
end
assign host_rst_filter = host_rst_d1 | host_rst_d2;
endmodule
滤掉大于1个周期且小于2个周期glitch的原理图如下:
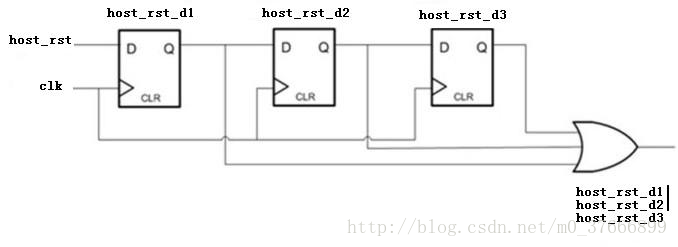
verilog代码实现如下:
module digital_filter_(clk_in,rst,host_rst,host_rst_filter);
input clk_in;
input rst;
input host_rst;
output host_rst_filter;
reg host_rst_d1;
reg host_rst_d2;
reg host_rst_d3;
always@(posedge clk_in or negedge rst)
begin
if(~rst)
begin
host_rst_d1 <= 1'b1;
host_rst_d2 <= 1'b1;
host_rst_d3 <= 1'b1;
end
else
begin
host_rst_d1 <= host_rst;
host_rst_d2 <= host_rst_d1;
host_rst_d3 <= host_rst_d2;
end
end
assign host_rst_filter = host_rst_d1 | host_rst_d2 | host_rst_d3;
endmodulePS:这是我自己采用的方式,上述方法消除毛刺是需要一定条件的,并不能保证一定可以消除。
版权声明:本文为CSDN博主「weixin_43343190」的原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/weixin_43343190/article/details/82961371