作者: 碎碎思,来源:OpenFPGA
这是新的系列教程,在本教程中,我们将介绍使用 FPGA 实现深度学习的技术,深度学习是近年来人工智能领域的热门话题。
在本教程中,旨在加深对深度学习和 FPGA 的理解。
- 用 C/C++ 编写深度学习推理代码
- 高级综合 (HLS) 将 C/C++ 代码转换为硬件描述语言
- FPGA 运行验证
在上一篇文章中,我们用C语言实现了一个卷积层,并查看了结果。在本文中,我们将实现其余未实现的层:全连接层、池化层和激活函数 ReLU。
每一层的实现
全连接层
全连接层是将输入向量X乘以权重矩阵W,然后加上偏置B的过程。下面转载第二篇的图,能按照这个图计算就可以了。
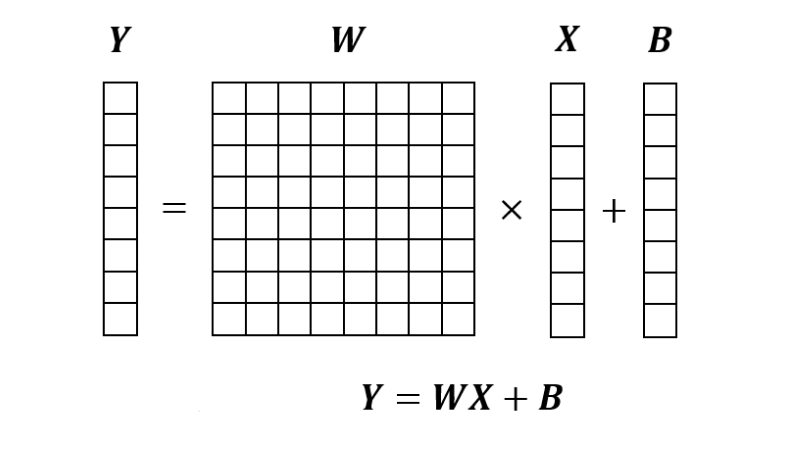
全连接层的实现如下。
void linear(const float *x, const float* weight, const float* bias,
int64_t in_features, int64_t out_features, float *y) {
for (int64_t i = 0; i < out_features; ++i) {
float sum = 0.f;
for (int64_t j = 0; j < in_features; ++j) {
sum += x[j] * weight[i * in_features + j];
}
y[i] = sum + bias[i];
}
}该函数的接口和各个数据的内存布局如下。
考虑稍后设置 PyTorch 参数,内存布局与 PyTorch 对齐。
输入
- x: 输入图像。shape=(in_features)
- weight: 权重因子。shape=(out_features, in_features)
- bias: 偏置值。shape=(out_features)
输出
- y: 输出图像。shape=(out_features)
参数
- in_features: 输入顺序
- out_features: 输出顺序
在全连接层中,内部操作数最多为out_channels * in_channels一个,对于典型参数,操作数远低于卷积层。
另一方面,关注权重因子,卷积层为shape=(out_channels, in_channels, ksize, ksize),而全连接层为shape=(out_features, in_features)。例如,如果层从卷积层变为全连接层,in_features = channels * width * height则以下关系成立。width, height >> ksize考虑到这一点,在很多情况下,全连接层参数的内存需求大大超过了卷积层。
由于FPGA内部有丰富的SRAM缓冲区,因此擅长处理内存访问量大和内存数据相对于计算总量的大量复用。单个全连接层不会复用权重数据,但是在视频处理等连续处理中,这是一个优势,因为要进行多次全连接。
另一方面,本文标题中也提到的边缘环境使用小型FPGA,因此可能会出现SRAM容量不足而需要访问外部DRAM的情况。如果你有足够的内存带宽,你可以按原样访问它,但如果你没有足够的内存带宽,你可以在参数调整和训练后对模型应用称为剪枝和量化的操作。
池化层
池化层是对输入图像进行缩小的过程,这次使用的方法叫做2×2 MaxPooling。在这个过程中,取输入图像2x2区域的最大值作为输出图像一个像素的值。这个看第二张图也很容易理解,所以我再贴一遍。
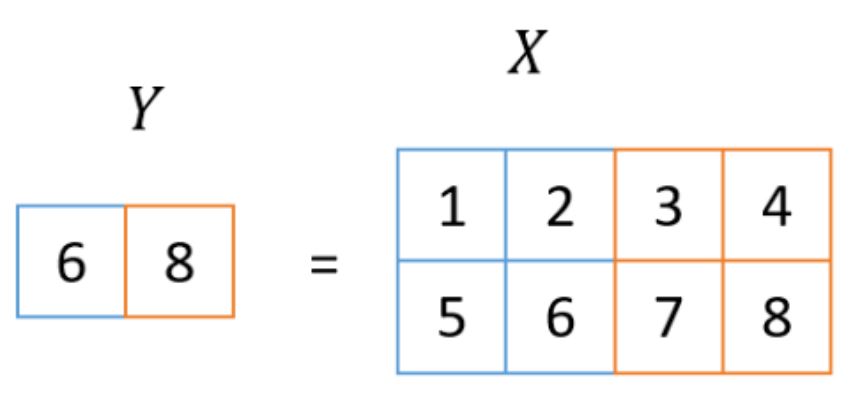
即使在池化层,输入图像有多个通道,但池化过程本身是针对每个通道独立执行的。因此,输入图像中的通道数和输出图像中的通道数在池化层中始终相等。
池化层的实现如下所示:
void maxpool2d(const float *x, int32_t width, int32_t height, int32_t channels, int32_t stride, float *y) {
for (int ch = 0; ch < channels; ++ch) {
for (int32_t h = 0; h < height; h += stride) {
for (int32_t w = 0; w < width; w += stride) {
float maxval = -FLT_MAX;
for (int bh = 0; bh < stride; ++bh) {
for (int bw = 0; bw < stride; ++bw) {
maxval = std::max(maxval, x[(ch * height + h + bh) * width + w + bw]);
}
}
y[(ch * (height / stride) + (h / stride)) * (width / stride) + w / stride] = maxval;
}
}
}
}这个函数的接口是:
此实现省略了边缘处理,因此图像的宽度和高度都必须能被stride整除。
输入
输出
参数
- width: 图像宽度
- height: 图像高度
- stride:减速比
ReLU
ReLU 非常简单,因为它只是将负值设置为 0。
void relu(const float *x, int64_t size, float *y) {
for (int64_t i = 0; i < size; ++i) {
y[i] = std::max(x[i], .0f);
}
}由于每个元素的处理是完全独立的,x, y因此未指定内存布局。
硬件生成
到这里为止的内容,各层的功能都已经完成了。按照上一篇文章中的步骤,可以确认这次创建的函数也产生了与 libtorch 相同的输出。此外,Vivado HLS 生成了一个通过 RTL 仿真的电路。从这里开始,我将简要说明实际生成了什么样的电路。
如果将上述linear函数原样输入到 Vivado HLS,则会发生错误。这里,将输入输出设为指针->数组是为了决定在电路制作时用于访问数组的地址的位宽。另外,in_features的值为778=392,out_将features的值固定为32。这是为了避免Vivado HLS 在循环次数可变时输出性能不佳。
static const std::size_t kMaxSize = 65536;
void linear_hls(const float x[kMaxSize], const float weight[kMaxSize],
const float bias[kMaxSize], float y[kMaxSize]) {
dnnk::linear(x, weight, bias, 7*7*8, 32, y);
}linear_hls函数的综合报告中的“性能估计”如下所示:
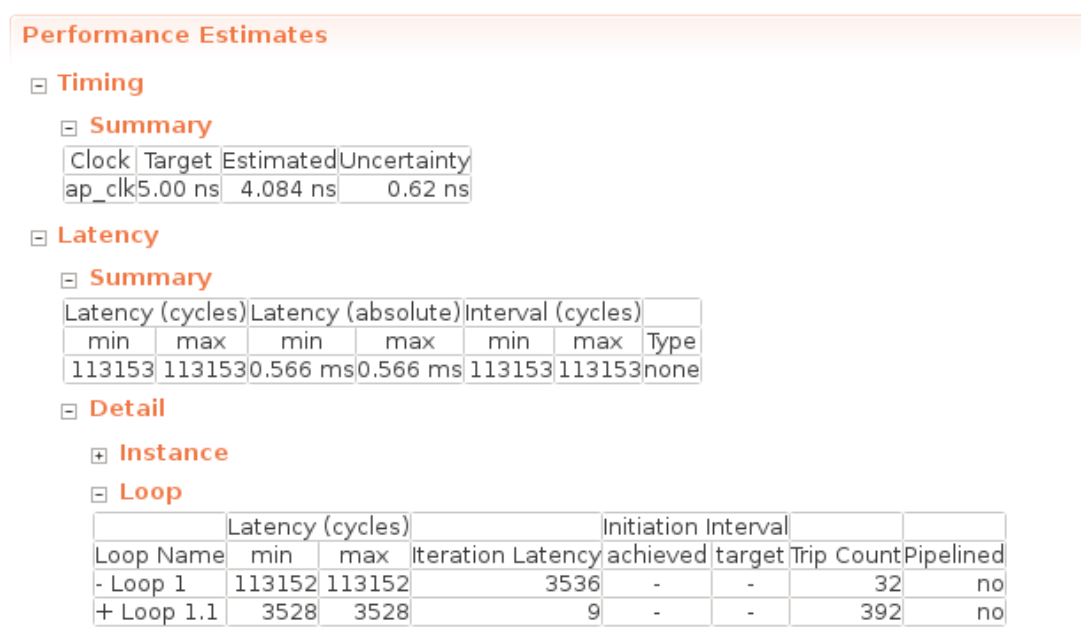
在Timing -> Summary中写入了综合时指定的工作频率,此时的工作频率为5.00 ns = 200MHz。重要的是 Latency -> Summary 部分,它描述了执行此函数时的周期延迟(Latency(cycles))和实时延迟(Latency(absolute))。看看这个,我们可以看到这个全连接层在 0.566 ms内完成。
在 Latency -> Detail -> Loop 列中,描述了每个循环的一次迭代所需的循环次数(Iteration Latency)和该循环的迭代次数(Trip Count)。延迟(周期)包含Iteration Latency * Trip Count +循环初始化成本的值。Loop 1 是out_features循环到loop 1.1 in_features。在Loop1.1中进行sum += x[j] * weight[i * in_features + j]; 简单计算会发现需要 9 个周期才能完成 Loop 1.1 所做的工作。
使用HLS中的“Schedule Viewer”功能,可以更详细地了解哪些操作需要花费更多长时间。下图横轴的2~10表示Loop1.1的处理内容,大致分为x,weights等的加载2个循环,乘法(fmul)3个循环,加法(fadd)4个循环共计9个循环。
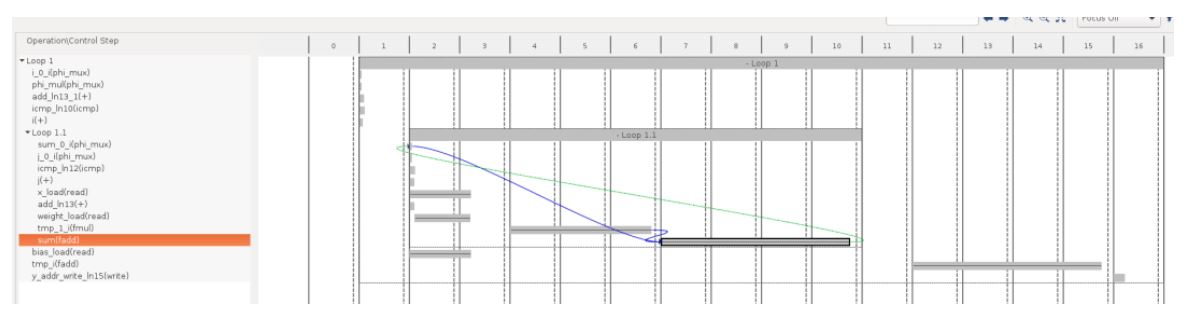
在使用 HLS 进行开发期间通过添加#pragma HLS pipeline指令,向此代码添加优化指令以指示它创建高效的硬件。与普通的 FPGA 开发类似,运算单元的流水线化和并行化经常用于优化。通过这些优化,HLS 报告证实了加速:
- 流水线:减少迭代延迟(min=1)
- 并行化:减少行程次数,删除循环
正如之前也说过几次的那样,这次的课程首先是以FPGA推理为目的,所以不会进行上述的优化。有兴趣进行什么样的优化的人,可以参考以下教程和文档。
教程:https://github.com/Xilinx/HLS-Tiny-Tutorials
文档:https://www.xilinx.com/support/documentation/sw_manuals/xilinx2019_2/ug902-vivado-high-level-synthesis.pdf
最后,该函数的接口如下所示。
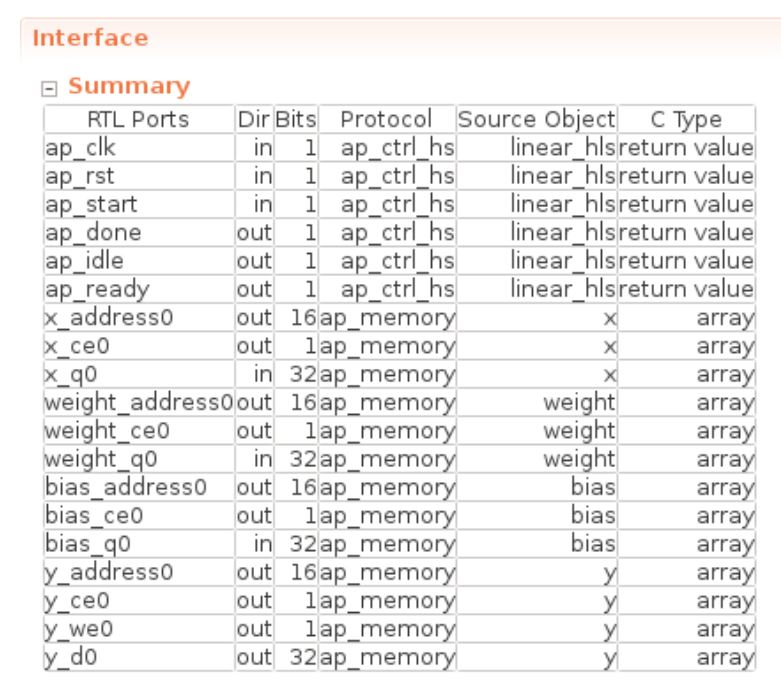
由于本次没有指定接口,所以数组接口如x_ 等ap_memory对应FPGA上可以1个周期读写的存储器(BRAM/Distributed RAM)。在下一篇文章中,我们将连接每一层的输入和输出,但在这种情况下,我们计划连接 FPGA 内部的存储器作为每一层之间的接口,如本例所示。
总结
在本文中,我们实现了全连接层、池化层和 ReLU。现在我们已经实现了所有层,我们将在下一篇文章中组合它们。之后我们会实际给MNIST数据,确认我们可以做出正确的推论。