文章来源:FPGA入门到精通
在当今数字化的时代,数字滤波器如同一位幕后的魔法大师,在众多领域施展着它的神奇魔力,悄然改变着我们的生活。
那么,究竟什么是数字滤波器呢?让我们一同揭开它神秘的面纱。
一、什么是数字滤波器?
1、模拟滤波器(Analog filter)
滤波器在模拟电路时代就已产生,按照频率响应的特性,选择性地通过或抑制输入信号中的特定频率成分,从而实现信号的频率选择性调节,比如常见阻容滤波器。
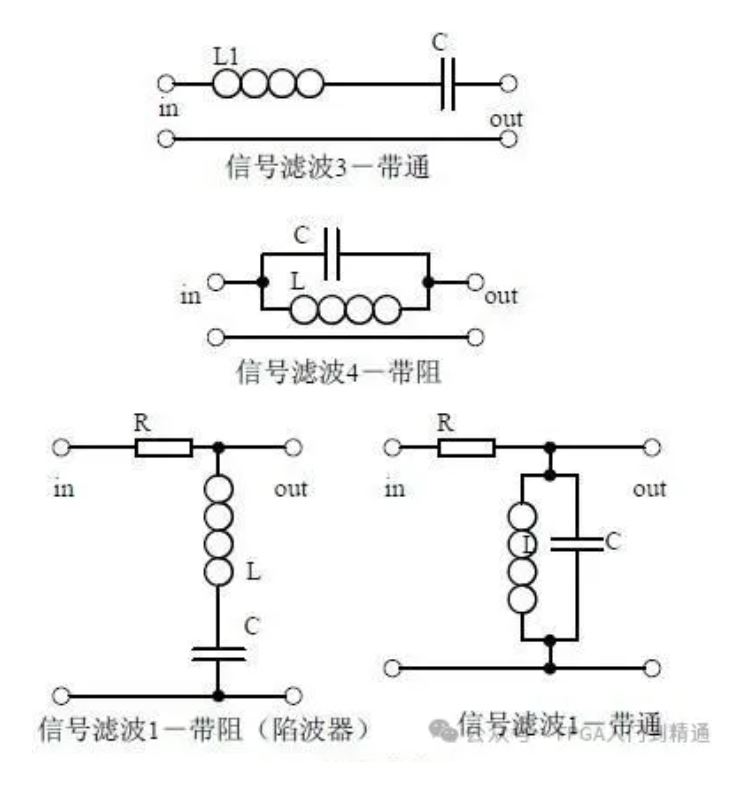
2、数字滤波器
数字滤波器,简单来说,就是一种对数字信号进行滤波处理的装置或算法。
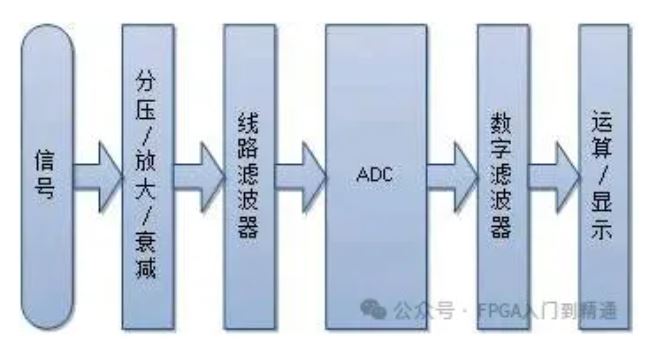
它以数字信号为输入,通过特定的运算规则,改变输入信号的频谱特性,从而实现对信号的滤波操作。
其基本原理是基于离散时间系统的特性,利用数字电路或计算机软件来实现对输入信号的处理。
与模拟滤波器相比,数字滤波器具有诸多显著优势:精度高、稳定性好、灵活性强。
二、数字滤波器的分类及特点
数字滤波器的分类方式多样,常见的分类包括:
1、按功能分类
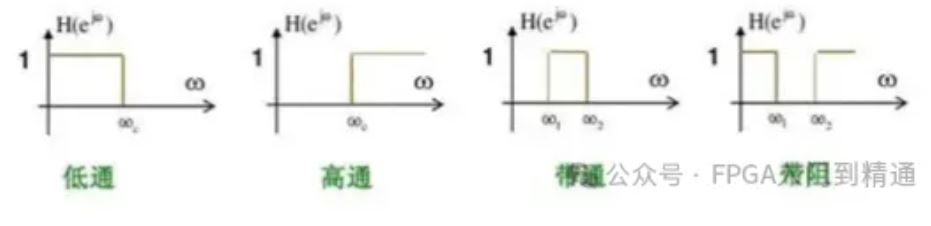
(1)低通滤波器
允许低频信号通过,而对高频信号进行衰减。
例如,在音频处理中,可用于去除高频噪声,使声音更加纯净。
(2)高通滤波器
与低通滤波器相反,它阻挡低频信号,让高频信号通过。
常用于去除信号中的低频干扰,突出信号的高频部分。
(3)带通滤波器
只允许特定频率范围内的信号通过,对范围外的频率进行抑制。
在通信领域,常用于选择特定频段的信号进行传输或接收。
(4)带阻滤波器
阻止特定频率范围内的信号,而让其他频率的信号通过。
可用于消除特定频率的干扰,如电力系统中对特定谐波的滤除。
(5)全通滤波器
对所有频率的信号都有相同的增益,但可能会改变信号的相位。常用于相位校正等特殊应用场景。
2、按实现的网络结构或单位抽样响应分类
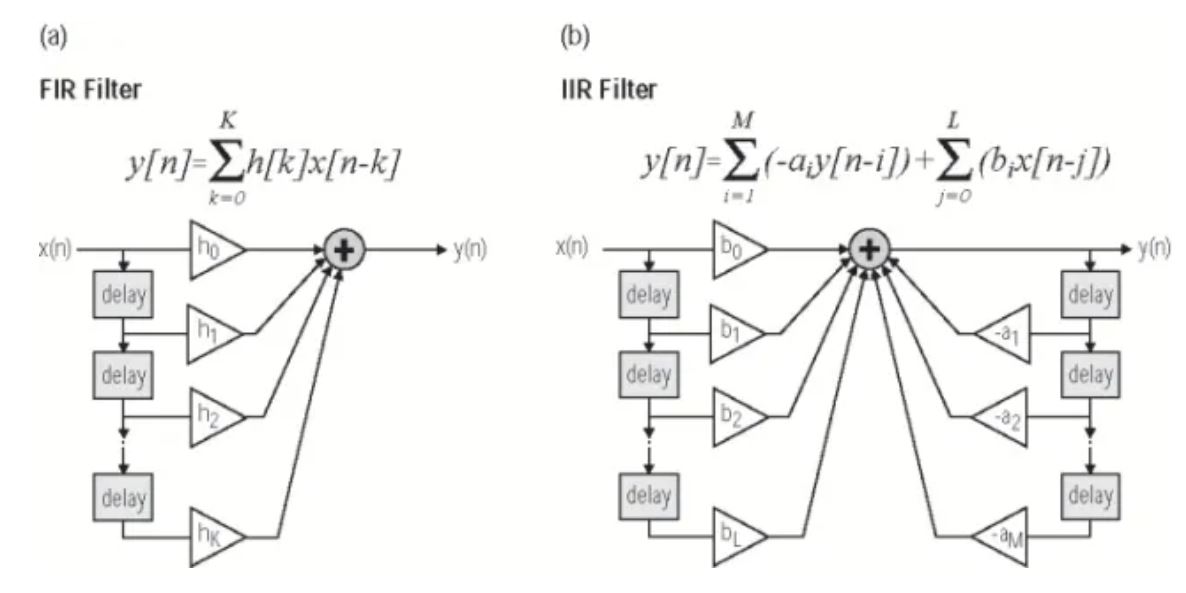
(1)无限脉冲响应(IIR)滤波器
具有反馈结构,冲激响应无限长。
IIR 滤波器能够提供更复杂的频率特性,在相同滤波性能要求下,通常所需的阶数较低,从而计算量较小、存储需求较少。
但是,由于存在反馈,可能会导致稳定性问题,并且在设计和实现过程中需要更加小心地处理极点位置,以确保系统的稳定性。
(2)有限脉冲响应(FIR)滤波器
冲激响应长度有限。
FIR 滤波器具有稳定性好、线性相位特性易于实现等优点。
线性相位意味着滤波器对不同频率的信号不会产生相位失真,这在许多对信号相位敏感的应用中非常重要,如通信系统中的高速数据传输、图像处理中的边缘检测等。
然而,为了实现与 IIR 滤波器相当的滤波性能,FIR 滤波器往往需要较高的阶数,这意味着更多的计算资源和存储需求。
三、数字滤波器的设计方法
数字滤波器的设计是一个复杂而关键的过程,不同类型的滤波器有不同的设计方法。
1、窗函数法
这是设计 FIR 滤波器的常用方法之一。
通过选择合适的窗函数,对理想滤波器的脉冲响应进行截断,以得到实际的滤波器系数。
常见的窗函数有矩形窗、汉明窗、布莱克曼窗等,不同的窗函数具有不同的频谱特性,会影响滤波器的性能。
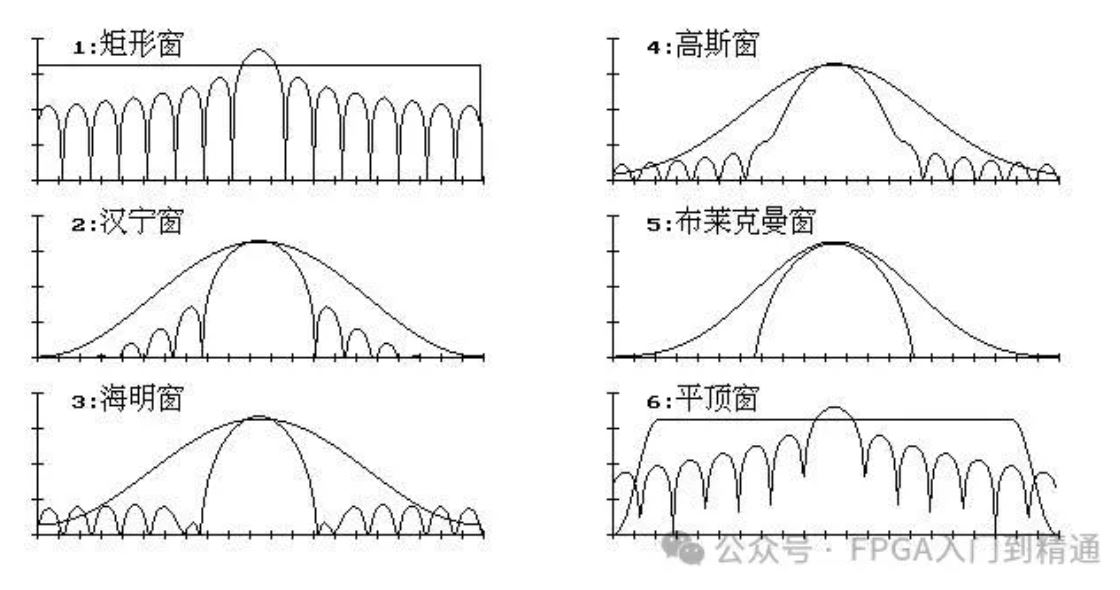
例如,矩形窗的主瓣宽度较窄,但旁瓣电平较高;汉明窗的主瓣宽度稍宽,但旁瓣电平较低,能够有效降低滤波器的旁瓣泄漏。
2、频率抽样法
该方法基于对滤波器频率响应的抽样来确定滤波器的系数。
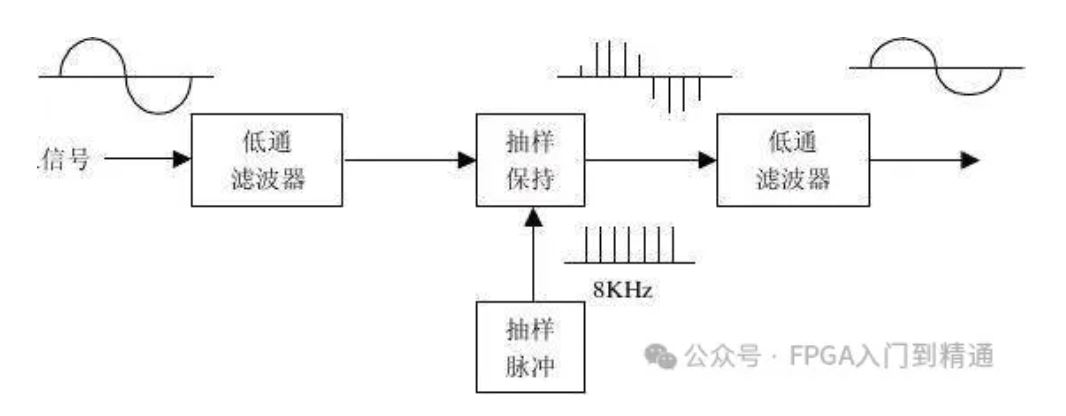
首先在频域上对所需的滤波器特性进行抽样,然后通过逆离散傅里叶变换(IDFT)得到滤波器的时域脉冲响应。
这种方法在设计特定频率特性的滤波器时较为方便,但可能会存在频率响应的误差,需要合理选择抽样点数来控制误差。
3、优化设计法
例如切比雪夫逼近法等。
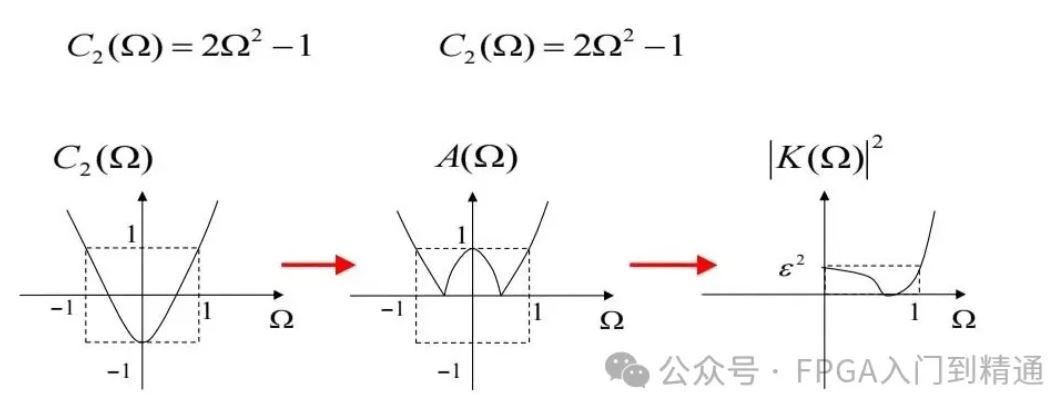
这种方法通过优化算法来寻找使滤波器性能指标最优的系数。
优化目标可以是最小化滤波器的误差、最大化滤波器的选择性等。
优化设计法通常需要较高的计算成本,但能够得到性能更优的滤波器设计。
四、数字滤波器的应用领域
数字滤波器的应用几乎无处不在,以下是一些主要领域:
1、通信领域
在无线通信系统中,数字滤波器用于信道滤波、信号调制和解调、抗干扰等。
例如,在手机通信中,滤波器可以对接收和发送的信号进行滤波处理,提高信号的质量和可靠性,减少多径衰落和噪声的影响。
2、音频处理
用于音频信号的降噪、均衡、混音等。
在音乐制作中,数字滤波器可以塑造声音的音色和频率特性,创造出各种独特的音效;
在语音识别系统中,滤波器可以去除背景噪声,提高语音信号的清晰度,从而提高识别准确率。
3、图像处理
可用于图像的增强、去噪、边缘检测等。
例如,通过低通滤波器可以去除图像中的高频噪声,使图像更加平滑;高通滤波器则可以突出图像的边缘和细节信息,有助于图像的分割和特征提取。
4、医疗领域
在医疗设备中,数字滤波器用于生物医学信号的处理,如心电图(ECG)、脑电图(EEG)等信号的滤波和分析。
可以去除信号中的噪声和干扰,提取有用的生理信息,为医生的诊断提供依据。
5、自动控制领域
用于控制系统中的信号处理,改善系统的性能。
例如,在工业自动化控制系统中,滤波器可以对传感器采集的信号进行滤波,消除噪声和干扰,提高控制精度和系统的稳定性。