本文转载自:FPGA技术联盟
1、前言
将浮点数定量化为定点数时,有一个避不开的问题:某些小数是无法用有限个数的2进制数来表示的。比如:

可以看到0.5是可以精准表示的,但是0.1却不行。原因是整数是离散的,而小数是连续的。在固定范围内整数的个数是有限个,而小数的个数则是无限个,所以某些小数注定是不能被有限个数的编码来精准表示的。
显然,在工程中不可能做无限位的定点化,我们只能根据需求,确定好精度从而决定定点数的格式。确定好定点数的格式后,有一个无法避免的问题,那就是如何对超过范围的部分进行处理,即如何舍入(Rounding)?
常见的舍入方式有向上取整(ceil),向下取整(floor),向0取整(fix),四舍五入(round)等等,本文只讨论四舍五入这种舍入方式。
2、10进制中的四舍五入
10进制的四舍五入大家都很熟悉了,比如:

假如有1个4位小数(整数2位)要舍入到2位小数(整数2位),例如 21.4567 >> 21.46 ,这类转换可以写如下的Verilog伪代码:

3、二进制中的四舍五入
2进制的四舍五入和10进制的原理是一样的。10进制的四舍五入,其中的4和5分别代表的是数据的上半部分04和下半部分59。2进制没有4和5,只有0和1,所以严格来讲,2进制的四舍五入应该叫 “0舍1入”。
首先对定点数的格式做如下约定:
. Qm.n 表示整体长度为m,小数部分长度为n的有符号定点数。例如,Q8.5表示 1bits符号位 + 2bits整数 + 5bits小数的有符号定点数
. UQm.n表示整体长度为m,小数部分长度为n的无符号定点数。例如,UQ8.5表示 3bits整数 + 5bits小数的无符号定点数
对于10进制的整数和负数的四舍五入,规则如下:
. -1.3四舍五入到,-1.5会四舍五入到-2,-1.8会四舍五入到-2
. 1.3四舍五入到1,1.5会四舍五入到2,1.8会四舍五入到2
比较需要注意的是0.5这类中间数据的处理规则:0.5四舍五入到1,-0.5四舍五入到-1。
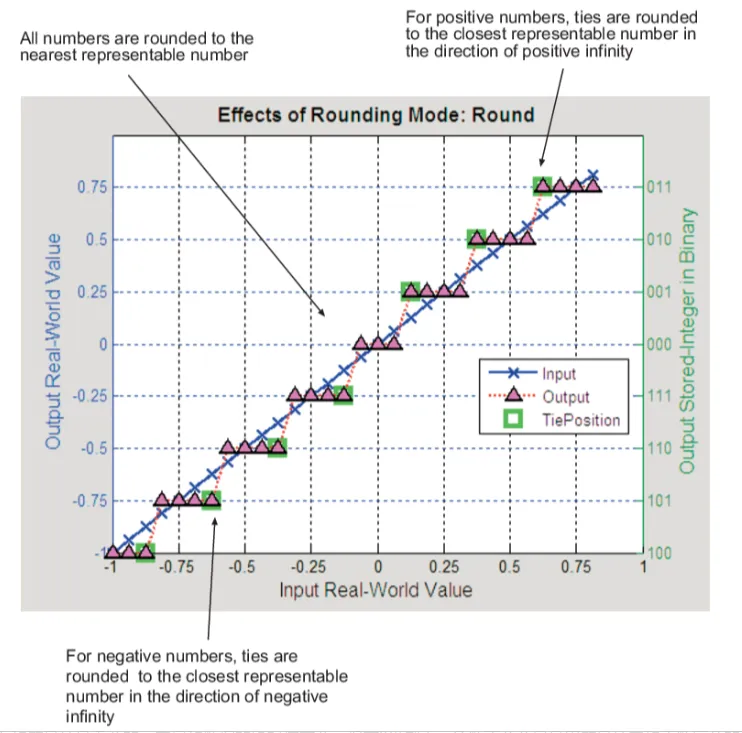
这说明四舍五入和符号位是无关的,它只和数据的绝对值有关。但在2进制中,负数不单单只是用符号位来和正数区分的,所以对于二者的处理还是有一些区别。接下来分别讨论。
3.1、无符号数的四舍五入
假设有一个UQ8.6格式的定点数要转换为UQ5.3格式的定点数,要求舍入模式为四舍五入(round)。即用四舍五入的方法保留3位小数,那么只需要判断第4位小数是否为1即可。若为1,则向第3位小数产生进位1,若为0,则向第3位小数产生进位0,其余小数部分舍去。例如

接下来就可以写Verilog代码了:

因为当次位的值是1时,就加1;当次位的值是0时,就加0。所以上面的写法和下面的写法是等价的:

接下来写个TB测试一下,把转换的结果保存在文本文件****里,后面再跟matlab的转换结果做比较。TB如下:

matlab对定点数的处理就方便很多了,主要需要用到两个函数 fi 和 hex。
. fi 可以生成一个/多个指定格式的定点数
. hex可以将定点数以16进制显示,方便写入文件
matlab代码如下(看注释吧):

这时就分别生成了两个文件:
因为这里数据量不多,所以我是直接打开两个文件用插件对比的,仿真结果有一点小小的问题,下面四个数据是对不上的:

左边是matlab的对照输出,右边是RTL的输出。这四个数据分别是二进制的:
. 11_111_100
. 11_111_101
. 11_111_110
. 11_111_111
matlab四舍五入后的结果是 0x1F 即5bits的11_111,而RTL的结果则是 0x00 即5bits的00_000,这是数据明显溢出了,因为我们没有设计对应的溢出保护机制,所以结果就出错了。关于溢出的几种处理方式在前两篇文章已经讲过了,这里就不讲了。
3.2、有符号数的四舍五入
讨论有符号数的四舍五入处理之前,需要先了解两个问题:
1. 如何根据有符号数的补码快速求得对应的数值?
2. 将定点数的小数部分截断,在数值上相当于什么操作?
(1)如何根据有符号数的补码快速求得对应的数值?
我相信很多人在把一个负数的补码转换成求其10进制数值时采取的方法是将其转化按位取反(除符号位外)+1,然后再把数值位都加起来。例如:

其实有更加简便的方法的,那就是让符号位也参与运算,但是权重是负的,例如:

(2)将定点数的小数部分截断,在数值上相当于什么操作?
例如通过直接截断方式把Q4.2格式的定点数转换成Q2.0格式的,实际上就是直接去除小数部分。去除小数部分,实际上就相当于在数值上向下取整(floor)。例如:

现在可以继续讨论如何实现有符号数的四舍五入了。
其实直接套用上面的方法也可以对有符号数做四舍五入,只是有一个例外,那就是对小数部分是0.5的这类数需要特殊处理。为了方便说明,接下来以Q4.2格式转Q2.0格式为例(实际上就是对小数做四舍五入)。

10_10(-1.5)和11_10(-0.5)这两个数按理来讲的四舍五入结果应该是:

如果用老办法,那就是 整数位直接加第1位小数的值 ,所以结果应该是:

虽然二者的处理结果是不同的,但也只是一个舍入到了左边的整数,一个舍入到了右边的整数,二者在精度上是一致的。如果算法不对这方面做特别的要求或者要求比较松,这种方法其实也是可以用的。这种方法最大的好处就是省资源,因为它不用判断0.5这类特殊情况嘛。
如果你希望严格遵守四舍五入的定义,那么我们接着分析。
从上面我们知道了,负数的最高位是可以参与加法的,所以计算一个负数的数值时,可以分为以下3种情况:
(1)要截掉的小数位的最高位为1,且剩余位全为0。
例如Q4.2转Q2.0,即xx.10,小数的最高位的值是0.5,剩余小数部分都是0则部分的和是0,相加说明小数的值为0.5,加上整数部分的值后,整个定点数应该是个x.5 类型的小数。
因为-1.5是舍入到-2(相当于向下取整)。所以这种情况的处理方式为:

例如1.5舍入到2,即01.10除去小数位即01,然后再加1即 01 + 1 =10(2);-1.5舍入到 -2,即10.10除去小数位即10,然后再加0即 10 + 0 =10(-2)。
(2)要截掉的小数位的最高位为1,且剩余位不全0
最高位为1表示的值是0.5,其他位不全为0,说明小数部分的值是(0.5,1),上面说过了,最高位的符号位是可以参加到数值的运算的,所以正数部分的值是个负数,整数 + 小数后 ,其小数部分的值的绝对值就处于(0,0.5)范围内了。比如:

因为这个范围内的值舍入都是向上取整的,例如 -1.25>> -1,-1.375>> -1。所以这种情况的处理方式为:

(3)要截掉的小数位的最高位为0
小数的最高位为0,说明整个小数的部分不会超过0.5,加上整数部分的负数后,整个定点数的值的小数部分的绝对值肯定在范围(0.5,1)。例如:

因为这个范围内的值舍入都是向下取整的,例如 -1.75 >> -2,-1.875 >> -2。所以这种情况的处理方式为:

可以采用与无符号数的转换类似的例子:

根据上面的分析,可以写如下的Verilog伪代码,首先出掉多余的小数位,并加上进位:

然后对不同的情况来判断应该加的进位值:

上面的判断可以简化一下:

综上,这部分的Verilog代码如下:

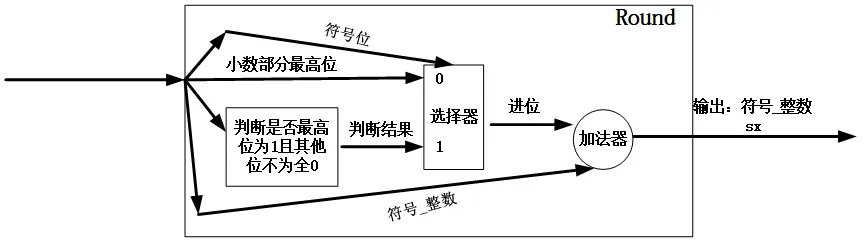
这一次,我们先用matlab生成所有的Q8.6格式的定点数和Q5.3格式的定点数,然后把Q8.6格式的定点数通过TB输入到RTL模块,观察RTL输出的Q5.3格式的定点数和matlab生成的是否一致,就可判断电路是否设计正确。
matlab部分代码如下:

然后编写TB,导入输入和输出,并将两个输出做比对,如果二者不一致则错误统计+1,最后观察错误个数即可。

仿真结果如下,有四个地方是对不上的:

和上面的无符号数的情况是一样,因为电路没有设计溢出保护,所以数据溢出了,因为matlab是有溢出处理的,所以二者的结果会对不上。