作者:FPGA入门到精通
在数字信号处理领域,滤波器是非常重要的工具,其中IIR(无限脉冲响应)滤波器以其独特的性能和应用场景,受到了广泛的关注。
今天,我们就来详细了解一下IIR直接型滤波器。
一、数字滤波器简介
数字滤波器从实现结构上划分,主要有FIR(有限脉冲响应)和IIR(无限脉冲响应 Infinite Impulse Response)两种。

FIR滤波器具有线性相位的特点,这意味着在设计者关心的通带范围内,它能保证输入信号的相位响应是线性的,即输入信号的延时特性以及各频率成分信号之间的相对相位是固定的。
IIR滤波器与FIR滤波器相比,在相同的幅频响应条件下,所要求的滤波器阶数明显比 FIR 滤波器低,需要消耗的硬件资源更少。
但IIR滤波器的另一个特点是不具备严格的线性相位特性,所以应用没有FIR滤波器应用广泛。
二、IIR滤波器原理
IIR滤波器的系统函数与差分方程如下所示:
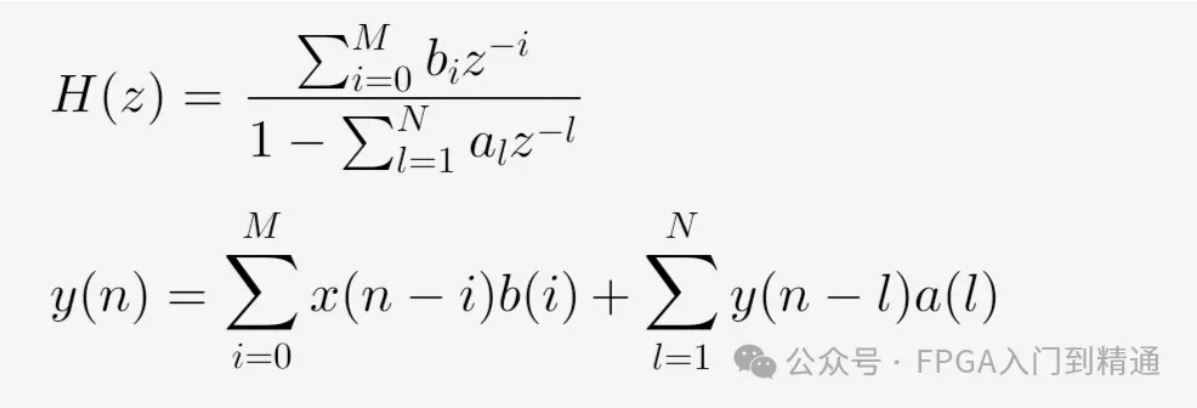
从差分方程可以看出,IIR滤波器存在反馈。这是它与FIR滤波器的一个重要区别。在FPGA设计时,必须要考虑到有限字长效应带来的影响。
IIR滤波器的结构有多种,比如直接I型、直接II型、级联型和并联型等,其中级联型结构准确性更好,且受参数量化影响较小,因此使用较广。
1、直接I型结构
直接I型结构直接由差分方程得到的。
从差分方程可以看出,输出信号由两部分组成:
(1)第一部分x(n-i)b(i)表示将输入信号进行延时,组成N节延时网路,这就相当于 FIR滤波器的横向网络,实现系统的零点。
(2)第二部分y(n-l)a(l)表示将输出信号进行延时,组成 N节的延时网络,每节延时抽头后与常系数相乘,并将乘法结果相加。由于这部分是对输出的延时,故为反馈网络,也就是系统的极点。
系统的信号流图,如下图所示:
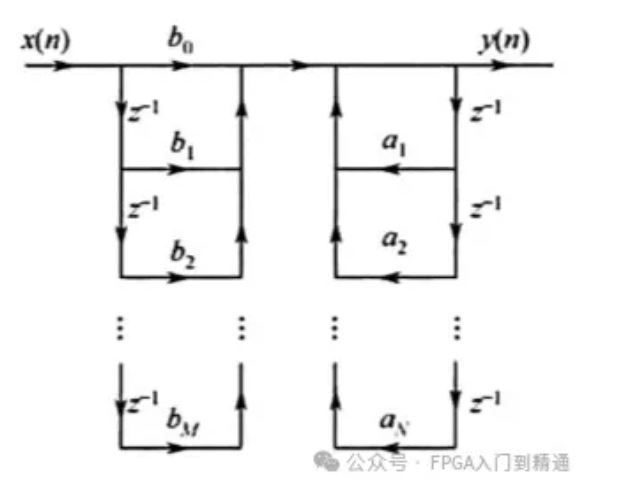
2、直接II型结构
如果从IIR的系统函数出发,视作两个系统的级联,并且合并公共的延时支路,得到的就是直接II型结构。
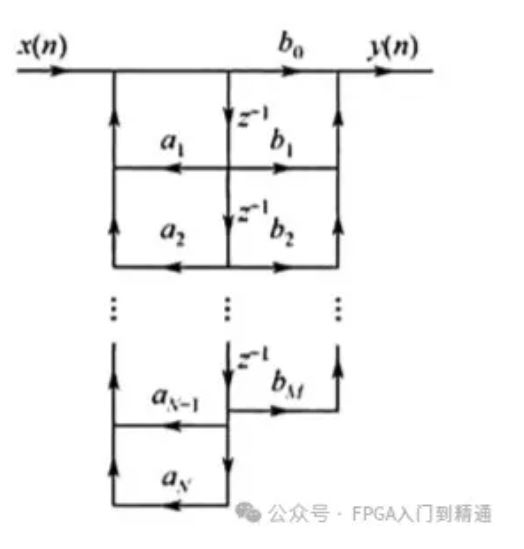
这种结构仅需要N个延时单元,在使用FPGA设计时采用直接II型结构可以节省一些资源。
三、Matlab设计IIR滤波器
使用matlab来设计滤波器,包括计算滤波器系数、滤波测试数据、滤波后数据等等,这里给出一个代码示例。
使用cheby2函数设计一个阶数为7(级数为8)的带通滤波器,采样频率为2000Hz,截止频率为500Hz、阻带衰减为60 dB。

输出结果:

新的差分工程:
512y(n) = 7[x(n)+ x(n- 7)]+ 21[x(n-1)+ x(n-6)] + 42[x(n-2)+ x(n- 5)]+ 56[x(n- 3)+ x(n-4)] - [-922y(n-1) + 1163y(n-2)- 811y(n- 3) +412y(n-4) - 122y(n- 5) + 24y(n-6)-2y(n-7)]
四、FPGA实现
零点滤波和极点滤波的实现,实际上可以看成是FIR滤波器,可以直接使用FIR滤波代码来实现。
顶层模块代码:
module direct_iir_filter( input clk, input rst, input [11:0] din, output [11:0] dout ); wire [26:0] x_out; wire [11:0] y_din; wire [26:0] y_out; wire [26:0] y_sum; wire [17:0] y_div; //实例化零点滤波系数 ZeroFilter u_ZeroFilter( .clk ( clk ), .rst ( rst ), .din ( din ), .dout ( x_out ) ); //实例化极点系数运算模块 PoleFilter u_PoleFilter( .clk ( clk ), .rst ( rst ), .din ( y_din ), .dout ( y_out ) ); //差分方程,零点滤波结果 - 极点滤波结果 assign y_sum = x_out - y_out; //因为滤波器系数中a(0)=512,除以512,即右移9位 assign y_div = y_sum[26:9]; //限幅处理 assign y_din = rst ? 0 : y_div[11:0]; //输出数据 assign dout = y_din; endmodule
零点滤波系数模块和极点滤波系数模块:
这两个模块都可以使用FIR滤波器计算实现,可以参考前面的FIR滤波器实现。
零点滤波系数模块可以成是一个7阶FIR滤波器,滤波系数是[170 21 4256 56 42 217]。
极点滤波系数模块可以成是一个6阶FIR滤波器,滤波系数是[512 -922 1163 -811 412 -122 24-2]。
滤波仿真效果图:
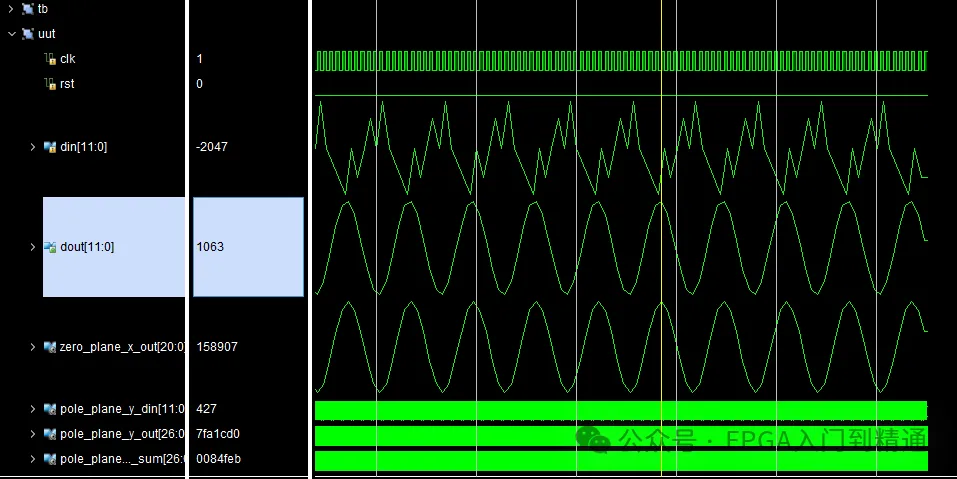
文章来源:FPGA入门到精通