文章来源：FPGA入门到精通
你是否好奇，一段嘈杂的录音如何被分离出人声和背景音乐？一张模糊的照片如何通过算法变得清晰？这一切的背后，都离不开一个关键数学工具——离散傅里叶变换（DFT）。
今天，我们用最通俗的语言，带你揭开它的神秘面纱！
一、DFT是什么？为什么它如此重要？
DFT全称离散傅里叶变换，是数字信号处理的核心工具。
简单来说，它能把一段随时间变化的信号（比如音频波形）转换成不同频率成分的组合，就像把一杯混合果汁分解出苹果、橙子各自的比例。
公式定义：
对于长度为N的离散信号x[n]，其DFT变换为：
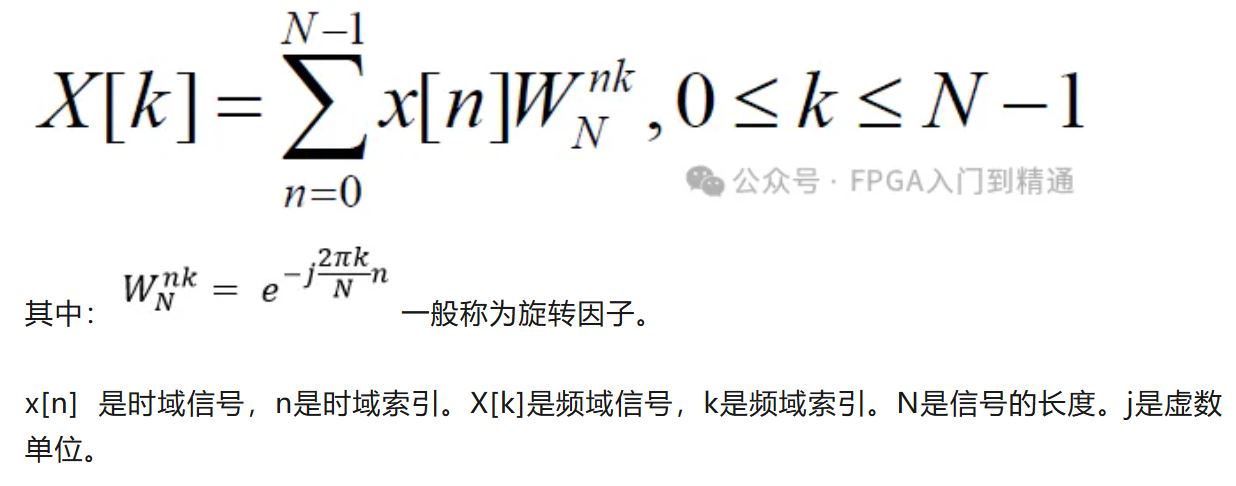二、DFT的三大核心特性
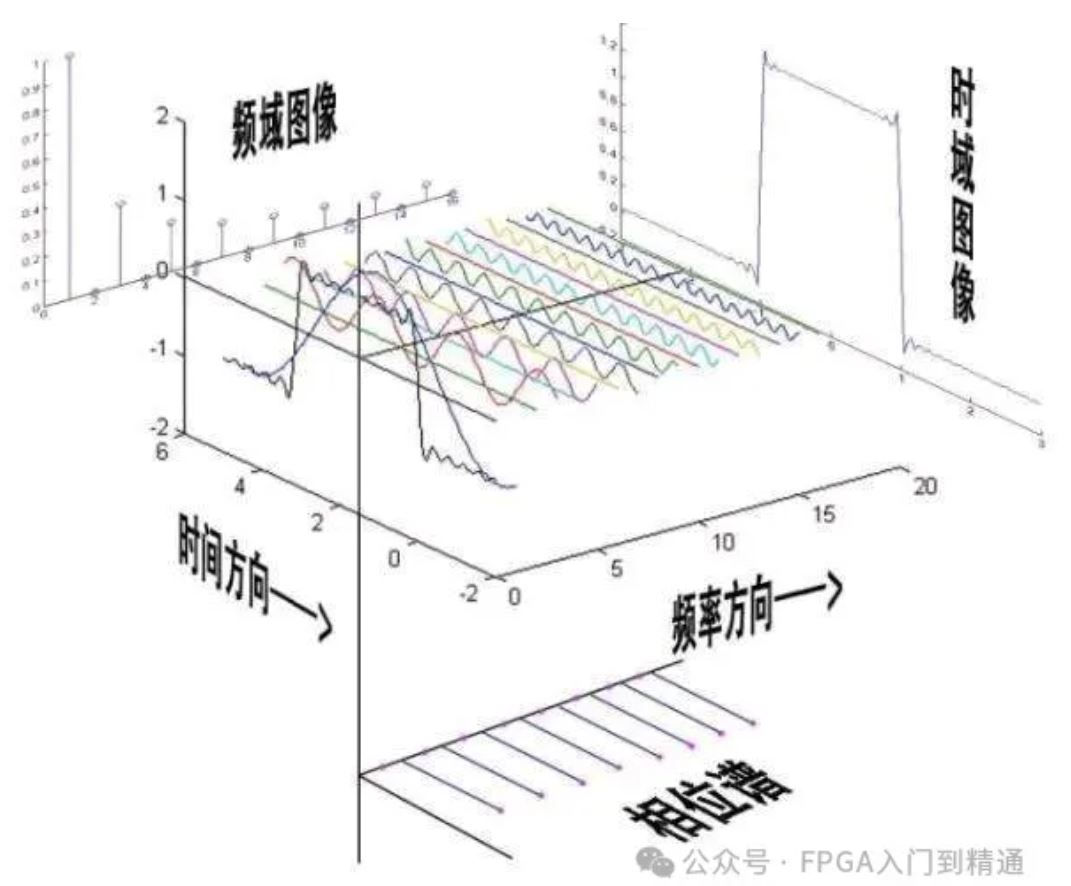
1. 频率分解将信号拆解为不同频率的正弦波，比如音乐中的高音、中音、低音。
将信号拆解为不同频率的正弦波，比如音乐中的高音、中音、低音。
2. 对称性
实信号的DFT频谱关于中点对称，高频分量在两端，低频在中间。
3. 快速计算
通过FFT算法（快速傅里叶变换），计算复杂度从O(N^2)降至O(N log N)，计算量大大降低。
三、DFT实战：从公式到应用
案例1：音频降噪
假设你录制的语音中有嗡嗡的电流声。通过DFT分析频谱后，找到噪声对应的频率k，将X(k)置零再逆变换回时域，噪音瞬间消失！
案例2：图像压缩
JPEG格式利用DFT将图像转换到频域，保留主要低频分量（人眼对高频不敏感），丢弃次要高频数据，实现高效压缩。
动手算一算：
对信号x[n] = {2,3,3,2}，做4点DFT：
最终4点DFT结果为：
- X(0)=10（直流分量）
- X(1)=-1 - j（第一个频率成分）
- X(2)=0（中间频率）
- X(3)=-1 + j（共轭对称）
四、DFT的局限与破解之道
1. 栅栏效应
DFT只能看到N个离散频率点，可能漏掉真实峰值。解决方法：补零增加DFT点数，让频谱“栅栏”更密。
信号截断导致频谱扩散。解决方法：加窗函数（如汉明窗）平滑信号边缘。
2. 频谱泄露
信号截断导致频谱扩散。解决方法：加窗函数（如汉明窗）平滑信号边缘。
五、DFT在生活中的无处不在
5G通信：OFDM技术利用DFT分解子载波，抗干扰传输数据。
医学成像：MRI通过DFT重建人体断层图像。
短视频滤镜：频域处理实现美颜、背景虚化。