10. 射频数据转换器品质因数与频率规划
10.1 噪声和杂散
在实际应用中,数据转换过程会产生噪声和杂散,它们会扭曲和干扰原始信号,影响系统的整体性能。
10.1.1 数据转换器噪声
在数据转换器中,通常讨论两个主要噪声来源:量化噪声和热噪声。在量化过程中,原始信号和离散信号中存在的误差叫做量化误差,如图10.1所示。

虽然量化噪声依赖于输入信号和数据转换器分辨率,但热噪声与这些因素无关,并且将始终存在于系统中。热噪声存在于所有电子元件中,是由数据转换器电路中的量子效应引起的。由于热噪声是数据转换器设计本身的产物,因此用户无法控制这种影响。热噪声可以通过测试仅使用直流输入信号的数据转换器的输出来轻松测量。
在低分辨率的数据转换器中,量化误差通常是噪声的主要来源。然而,随着分辨率的提高,热噪声变得更加突出。其他噪声源也会干扰数据转换器,如时钟噪声和放大器噪声。然而,由于这些噪声源来自与数据转换器分离的组件,因此可以通过良好的电路设计来降低它们的影响。
值得注意的是,RF-ADC的主要噪声源是时钟抖动,即时钟周期之间的时钟周期变化。对于这个问题,RFSoC板使用专用的时钟基础设施,其中包含多个时钟调节链,以尽可能地减少抖动。例如,ZCU208和ZCU216 RFSoC开发板使用单独的时钟子板CLK104,它使用两个参考时钟,抖动清除器和时钟合成器为数据转换器创建必要的时钟信号。
噪声通常与满量程输入信号的功率有关,通常为正弦波。信号功率和噪声功率之间的总体比率是信噪比(SNR)。
10.1.2 谐波失真
谐波失真是由数据转换器信号路径中的非线性引起的。这些非线性导致产生额外的频率分量,称为谐波,它在数学上与输入信号通过关系相关。

在考虑孤立的数据转换器,即忽略外部元件的影响时,设计人员可以参考制造商的数据表来了解谐波性能的信息。通常,在数据转换器规格中只说明前两个谐波,因为它们往往占主导地位。用于描述数据转换器的常用测量方法是总谐波失真( THD)。THD定义为所有谐波分量之和的功率与输入信号功率之比。通常只考虑前6次谐波,不考虑直流分量。
10.1.3 ADC交织杂散

交织ADC中的增益和相位失配与输入信号的频率相关,因此这些杂散的位置与信号频率成分有关。增益失配是指交织ADC的幅值差异,而相位偏移是指他们之间的时序差异。增益和相位失配产生杂散的位置为:

由于低阶谐波与内部ADC时钟频率混合,也存在额外的交织杂散。这些杂散的频率为:

10.1.4 时钟脉冲

数据转换器时钟也会引入它们自己的杂散,这些杂散取决于电路设计和时钟质量,很难量化。一种易于计算的杂散是锁相环混合产物,这些杂散的产生是由于时钟信号与输入信号混合,这种效应导致脉冲发生在:
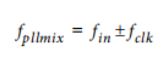
10.1.5 带宽限制信号的杂散发射
到目前为止,我们只考虑了与单频输入信号有关的杂散的频率含量。通常,通信信号包含若干频率,这些频率构成信号带宽。因此,与输入信号相关的任何杂散也将具有相对带宽,从而增加了它们引起干扰和失真的机会。此外,信号带宽越大,杂散重叠和干扰的可能性就越高。
在带宽有限的通信信号情况下,谐波失真产生的是谐波带而不是单音。一般来说,谐波是输入信号频率的倍数,由此产生的谐波带也是如此。因此,谐波带的带宽是原始信号贷带宽的倍数,二阶谐波是带宽的两倍,三阶谐波是带宽的三倍,以此类推,如图10.5所示。
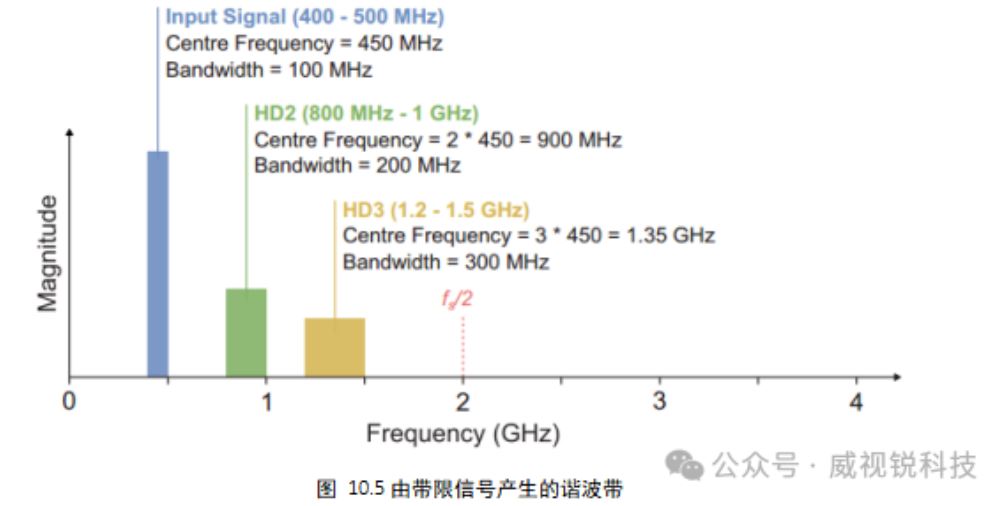
对于DAC,杂散频带占据了频谱很大一部分,必须在到达天线之前过滤掉,以避免对其他无线电信号产生干扰。对于ADC和DAC,频率成分高于奈奎斯特速率的杂散将混叠到第一奈奎斯特区,并可能干扰或扭曲感兴趣的信号。RF采样数据转换器的好处是能够通过过采样来减少上述影响,将在后续详细讨论。
10.2传统数据转换器特性
10.2.1 无杂散动态范围(SFDR)
无杂散动态范围是通信应用中的一个重要指标。SFDR测量数据转换器相对于奈奎斯特频带中存在的各种杂散分量的可用动态范围。它被定义为输入信号的RMS值与目标带宽中存在的最大杂散的RMS之比,即:
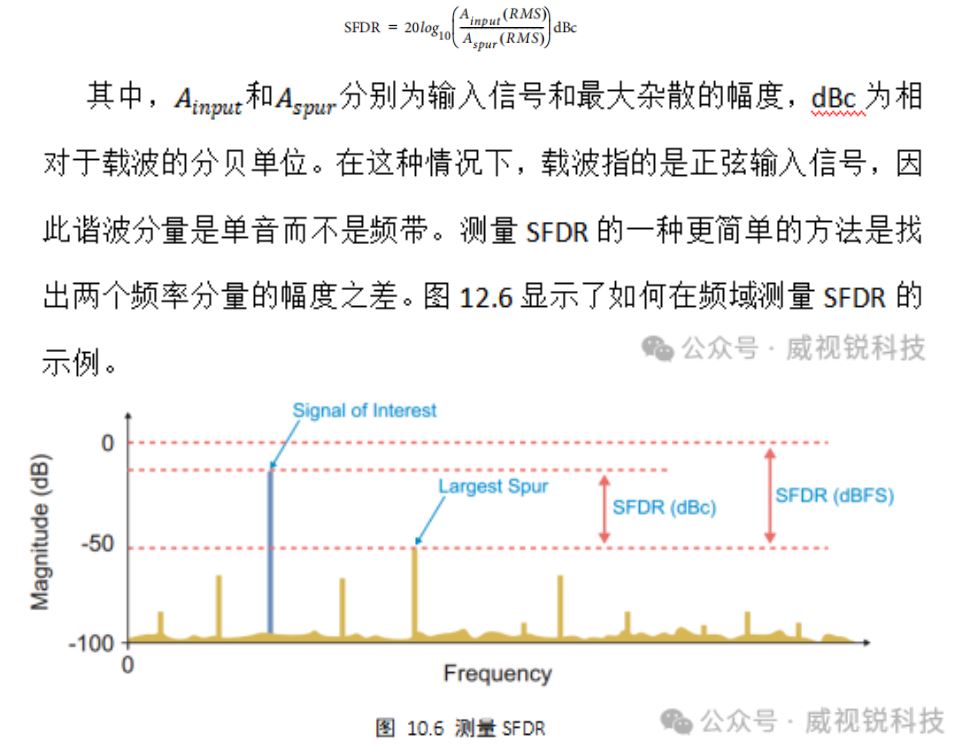
当输入信号在满量程时,谐波分量往往是最大的杂散。然而,随着输入信号幅度的下降,其他杂散会变得更加突出。SFDR度量将所有杂散分量考虑在内,并且SFDR测量排除谐波也是常见的。除此之外,由于杂散的幅度可能取决于输入信号频率,因此SFDR测量通常针对不同的输入频率。例如,第一代 RFSoC器件的数据表提供了240 MHz, 1.9 GHz, 2.4 GHz和3.5 GHz的SFDR测量,不包括二阶和三阶谐波。
10.2.2 信噪比
信噪比(SNR)为输入信号的功率与总噪声功率之比,其中不包括任何谐波或其他杂散成分。

由上式可知,随着噪声功率的减小,信噪比值增大。若信号和噪声功率相等,则信噪比为0dB。数据转换器信噪比有时也表示为:

其中N为数据转换器的分辨率,以位为单位。信噪比随着数据转换器分辨率的增加而增加。例如,一个12位数据转换器的信噪比为74 dB。但是,该式为理想的情况,只考虑数据转换器的量化噪声,而不考虑任何其他噪声源。因此,这个方程有时被称为信号量化噪声比(SQNR)。其次,该方程假设输入信号的均方根值处于满量程幅度,如果输入信号小于满量程,则必须添加一个附加项。

随着采样率相对于输入信号带宽的增加,信噪比也成比例地增加。这对RFSoC等器件具有积极的影响,因为高采样率可以大大提高信噪比。实际上,采样率每增加一倍,信噪比就会增加3dB。需要注意的是,当增加采样率时,噪声的总能量保持不变。然而,随着噪声在更宽的带宽上传播,其密度下降,如图10.7所示。也就是说,由于过采样信号的带宽现在占用更少的奈奎斯特带,因此可以滤波或抽取以降低总噪声能量。
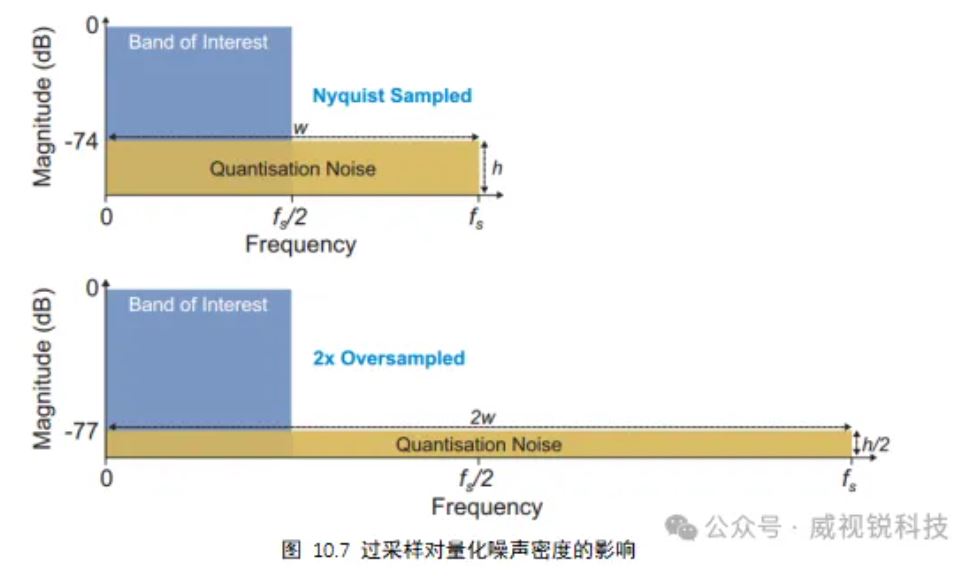
10.2.3 信干噪比
信干噪比是通信系统中重要的测量指标,通常简称为SINAD或SNDR。它不仅包括所有的噪声分量(量化噪声、热噪声等),还包括所有其他的频谱分量,如谐波、交织杂散等。它被定义为:

其中,为输入信号的功率,为噪声功率,为不含直流的总谐波失真(THD)。因此,SINAD给出了数据转换器动态性能的全面测量。
10.2.4 有效位数
有效比特数(ENOB)是数据转换器在整个奈奎斯特频带内能够实现的整体动态范围的测量。最好的情况是数据转换器的分辨率和它的ENOB是相等的,但在实践中通常不是这样。例如,一个数据转换器可能被宣传为具有10位的分辨率,但由于本章讨论的噪声和频谱成分,其实际分辨率可能只有8.5位。通常使用下式表示ENOB与SINAD的关系:
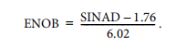
10.2.5 传统指标的局限性
本节中讨论的传统特性假设带宽接近奈奎斯特速率,它们与在RF频率下工作且具有高过采样率的数据转换。用于表征射频数据转换器性能的测量量如下:噪声频谱密度、互调失真和相邻信道泄露。
文章来源:威视锐科技