本文转载自: AI加速微信公众号
问题的提出
LSTM是一种循环神经网络,它解决了以往RNN中存在的长期依赖问题(采用门控信号来避免梯度消失和爆炸,同时增强了对过去信息的记录能力),现在被广泛的应用于NLP领域。LSTM也是一个多层网络,在实际应用中网络会更复杂一些,比如在语音识别中多层LSTM前往往还有对于语音信号的提取(包括FFT,离散余弦变换等)。一层的LSTM表达式如下所示:
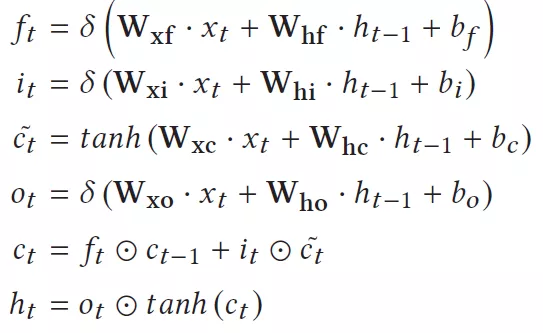
通过这个公式我们可以总结出LSTM计算本身的一些特点:
1 算子比较简单,计算算子有矩阵乘法,向量加法和乘法,激活函数(sigmoid/tanh),还有一个隐含的控制算子:循环和无条件跳转控制。循环控制来自于时间维度对x和h的计算,无条件跳转来自于不同LSTM层之间的切换;
2 参数量巨大,有8个不同的权重,以及4个偏置。权重通常都很大,因为一般LSTM的维度很大,比如对于一个1024维的LSTM层来说,其参数大小是8x1024x1024x2B(int16)=16M bytes。假设我们的DDR带宽能够达到80GB/s,加载一层的权重需要的时间为0.2ms左右。因此我们可以对这些巨大的参数对整个网络的延时所带来的影响有一个基本的理解。而一个网络的输入帧数通常都很大,因此帧数越多加载权重带来的时间开销也是线性增加的;
3 参数缺乏共享。权重参数只在时间维度上是共享的,但是在同一个时间点下的计算没有任何共享,即和x以及h的矩阵乘法中,每个权重参数只被使用一次,这个带来的后果就是参数复用率低,造成对off-chip和on-chip的带宽需求大;
4 计算存在内部依赖和外部依赖。Ht和ct的计算需要上一帧ht-1以及ct-1的数据,这是外部依赖。导致了无法在时间维度上实现ht和ct的并行计算。同时ht和ct又依赖于内部的中间结果,因此在LSTM内部ct和ht的计算必须在it,gt,ot计算之后。因此内部的并行性也受到了限制;
5 非线性函数的计算时间长,不太利于硬件的实现,所以通常是经过一些近似处理,比如线性化或者查表的方式,这种近似可能带来网路精度下降;
为了更好的实现LSTM的硬件加速,第一个要解决权重参数量大和有限带宽的矛盾,第二个需要处理好LSTM计算数据流,最后就是加速器设计本身的通用性支持。目前学术界以及产业界的解决方案主要有两种:一是定制化解决方案,一种是通用型解决方案。本章介绍定制化的解决方案。
定制化LSTM加速器
这类加速器通常将算法和硬件结构紧密结合,在算法层面通过剪枝,量化实现模型压缩,在硬件层面构建一个基于定制化数据流的LSTM计算结构。定制化结构能够最大限度利用算法压缩和硬件pipeline的优势,将网络性能发挥到极致,缺点是扩展性和可移植性较差,适合于网络模型固定或者变化较小的自有业务中。比如某一个固定功能的终端产品中,或者在数据中心针对某项固定模型的加速业务。
1. 权重稀疏化
在这种定制化LSTM加速器中,设计核心几乎都围绕着权重的剪枝和量化。正如前面所述,权重参数量巨大,无参数共享。其剪枝和量化可以大大提高整个网络的推理速度。LSTM中的矩阵计算是一个FC层网络,其剪枝位置包括输入通道剪枝和神经网络节点的剪枝。输入通道剪枝可以根据权重的某个阈值来去除那些对结果不重要的权重,其可以实现对权重矩阵的精细稀疏化操作。神经网络节点的剪枝即依据每个节点的结果,移除产生的输出不重要的节点。节点剪枝将权重矩阵的一行进行移除,保持了权重矩阵的对齐特性。节点剪枝可以更大的压缩权重参数量,而且可以保持tensor计算的对齐特性,有益于硬件的实现,但是其可能导致网络精度的下降。输入通道的剪枝位置具有精细调控参数,不对称的特性,其能够最大程度保持网络精度,但是由于其对权重矩阵稀疏化位置较为随机,往往造成硬件实现过程中有效计算不能够很好的对齐,造成计算资源的浪费。
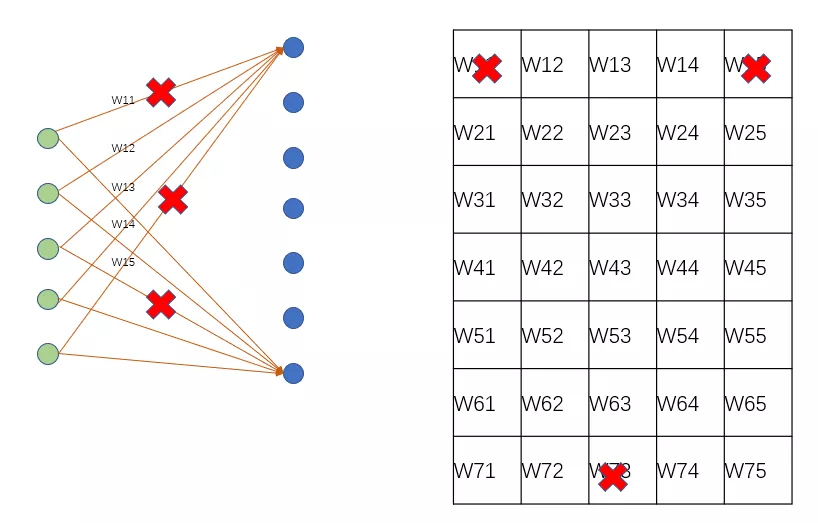
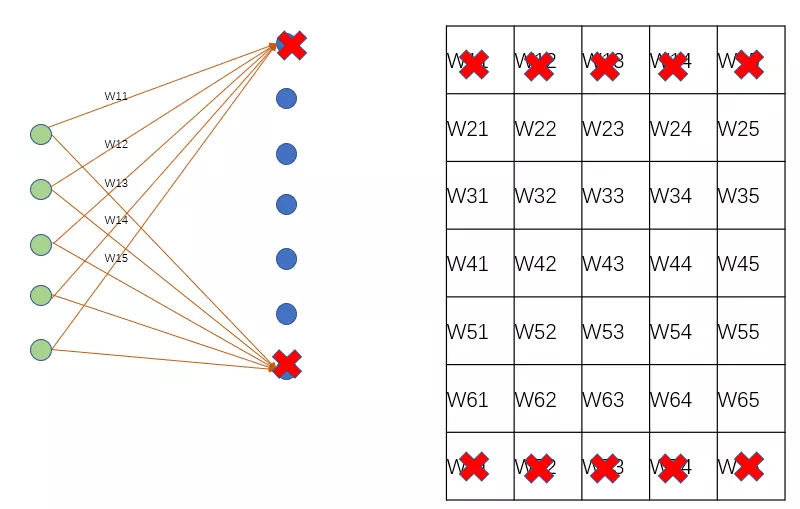
为了解决权重矩阵稀疏化导致的数据不对齐问题,一般在进行稀疏化的过程中施加一定的约束,保持一定的权重矩阵规则性。
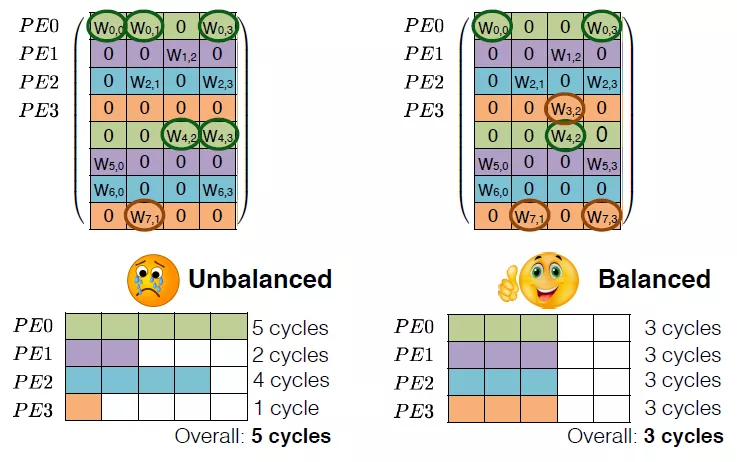
比如在文献[1]中,为了实现不同PE之间加载权重的balance,作者在稀疏化权重的时候,限制了对应相同PE的权重的剪枝数量。如果能够保证每个PE对应有效的计算元素是相同的,那么每个PE的有效计算量就是相同的,就避免了由于每个PE可能存在一些无效计算。比如下图,同一个颜色块用于同一个PE计算,那么所有PE的计算时间取决于有效数据最多的PE块,即5个cycle。如果采用平衡策略,那么保证了每个PE的有效数据都是3个,总的cycle就是3。在对权重矩阵稀疏化的过程中,权重可裁剪的阈值是需要根据有效权重数量进行动态调整的。比如原本在阈值之上的W01被去除,而原本在阈值之下的W43被保留。这样看来,权重中阈值是和PE相关的,如果PE对应的权重整体分布于较高值,那么阈值就相应增大,如果权重分布于较低值,阈值就相应减小。这样保证了对应每个PE的权重裁剪数量相同。
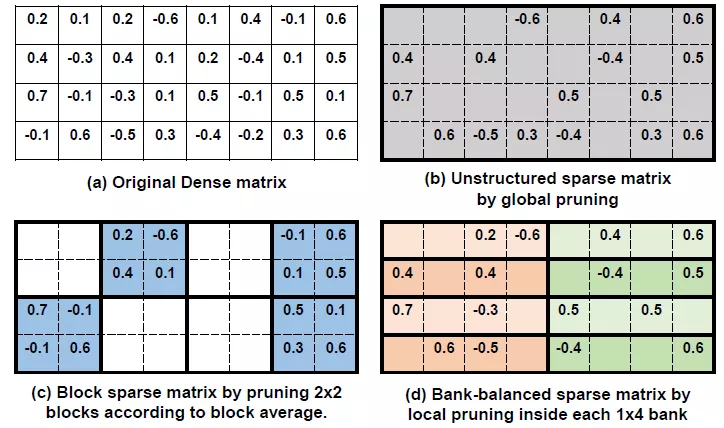
也有更为粗糙的权重稀疏化方法,在[2]中,对权重进行块稀疏化,即比较子矩阵中最大权重值和阈值大小,低于阈值的整个子矩阵都会被裁剪。整个过程如下图:

稀疏化后的权重矩阵分布更加规则,更有利于硬件的实现。相比于文献[1],这种方法施加了更强的限制,导致权重分布发生很大的变化。这可能造成网络精度的较大损失,同时带来了训练过程的复杂,需要调节多个hyper-parameter来满足精度需求:都是和阈值相关的,包括起始裁剪的iteration,增加阈值的起始iteration,停止裁剪的iteration等。除此之外,作者还对loss施加了权重的L2正则化约束,即对每个block中的权重进行L2norm计算,因此在训练过程中,L2 norm较大的block的权重会趋向于更大值,而较小L2值的block中权重会不断趋向于更小值。结合prunning可以更好的稀疏化权重并能保持网络精度。
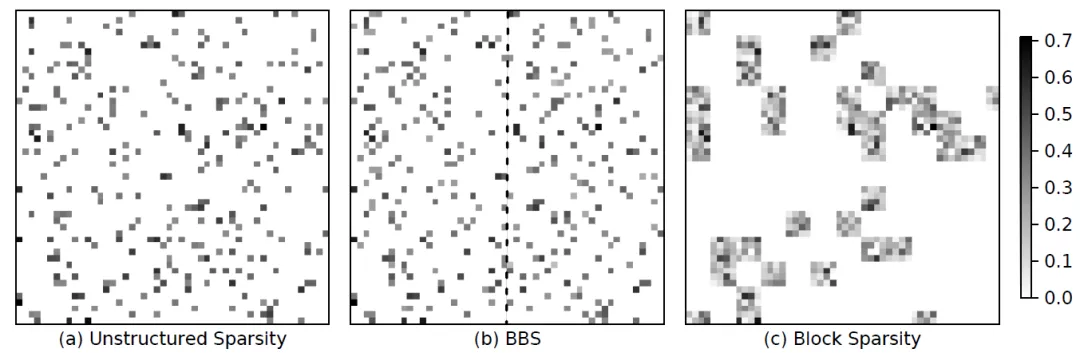
文献[3]中采取了更为缓和的裁剪策略:将一行权重分成多个bank,然后要求每个bank中裁剪数量相同。因此当硬件计算可以设计为按照每个bank计算的时候,这种权重分布对PE计算也是友好的。硬件上可以探索不同bank之间和bank内部的数据并行计算。同时其训练过程也比上一种方法简单了很多,在pre-trained model基础上逐渐提高prunning 比率来达到精度保持同时裁剪量最大。通过对权重的分布变化来看,bank-balance方法的权重分布变化很小,这也是其精度得以保持的原因。这里有几个超参数需要调节:权重矩阵中每行的bank数目,稀疏比率,阈值。Bank的数目受到硬件设计结构的制约,稀疏比率决定了bank中阈值的大小。算法描述见下面。

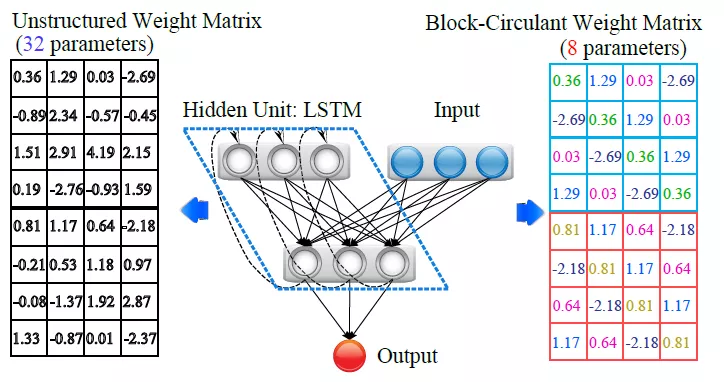
还有一种更具有技巧性的方法[4],作者利用了circular-matrix的特点,对权重矩阵分块,然后将这些块转换为circular-matrix。Circular-matrix是这样的矩阵:矩阵的每行/列的元素分别是上一行/列元素的偏移。因此circular-matrix中有效的矩阵元素只是一行/列的数目,这将2次幂参数量降低到1次幂。因此被分块成circular-matrix的权重矩阵大小取决于circular-matrix的大小,如果circular-matrix越大,那么权重矩阵参数量就被减小的更大,但是circular-matrix越大会导致网络精度的降低。因此需要寻找到一个合理的circular-matrix大小来在保证精度的前提下最大限度降低权重数据量。如果circular-matrix大小为1,那么权重矩阵保持不变,如果circular-matrix大小等于权重矩阵,那么原来的权重矩阵(nxn)会被减小的n个有效数据。
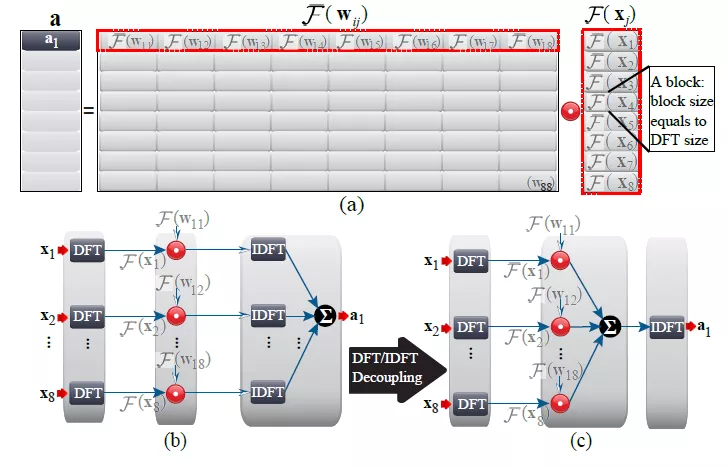
权重矩阵被转化为多块circular-matrix后,权重数据量大大降低,但是运算量并没有减少。但是circular-matrix乘法等效于卷积计算,因此将circular-matrix进行傅里叶变换后,卷积计算转换为element-wise乘法,这样卷积计算量被大大降低。虽然增加了离散傅里叶变换操作,但是可以采用快速傅里叶变换,最终总的计算量是降低的。经过作者的推算,一个被分割为pxq个circular-matrix(kxk)的权重矩阵,在做傅里叶转换后的计算量将由原来的pqk^2降低为pqklog(k)。并且权重的FFT可以被预先计算作为最终硬件使用的参数,那么硬件中只需要实现vector(x和ht)的FFT变换以及矩阵计算输出(W*x, W*h)的傅里叶反变换(IFFT)就可以了。W11,W12等是circular-matrix块,这些块的矩阵乘法将被转换为element-wise乘法。
2. activation稀疏化
在上一节中我们提出了对神经网络节点的剪枝,这需要来判断W*x的输出值,如果其重要性较低(即低于某个阈值),那么整个一行的权重矩阵元素都可以被裁剪。这种方法也是一种activation稀疏化方式。这种方法可以适用的前提是W矩阵中某一行的权重值都比较小,等效于将W按照行为块进行组织,然后进行块的裁剪优化。
还有一种activation稀疏化的方法,即对RNN网络中的x和ht进行裁剪[5]。其处理方法是这样的:
1 对于具有强时间相关性的RNN网络输入数据,其数值随时间变化缓慢,可以利用整个特性降低有效x和ht的数据量和计算量;
2 设置一个阈值,根据x或者ht变化的大小,选择保留前一时刻的值还是使用新值,即:
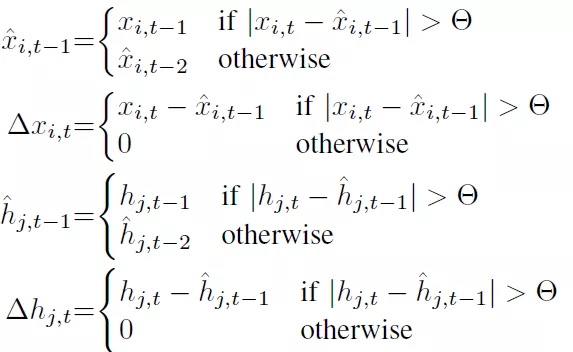
带有上标的为当前时刻的近似值,如果当前数值在以前一刻近似值为圆心,theta为半径的圆内,那么就使用前一时刻的值,如果不在圆内就使用当前时刻值作为近似值。然后求取相邻时刻近似值的差值,对于强时间关联性的信号就会出现大量的0值。这就为矩阵的优化计算提供了方便;
3 计算W*x可以用计算W*(xt-xt_1)来替代:
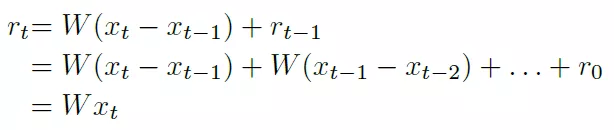
那么LSTM网络计算就可以描述为:
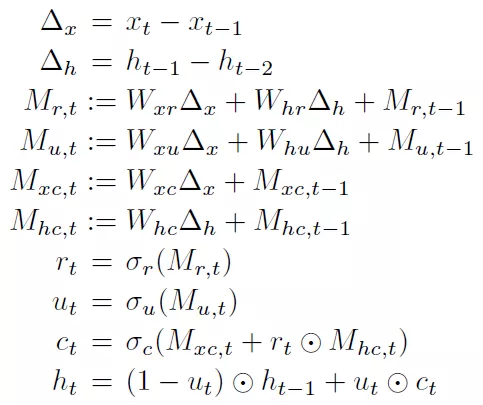
利用delta输入的特征,为0的值可以免除矩阵计算,这样大大降低了矩阵计算量;
4 虽然权重使用的总量没有减少,但是由于delta输入的特征,如果经过精心的设计,也可以在一定程度上减少对权重数据的加载。比如我们可以统计权重数据的使用频次,对于使用次数较多的weights,可以将其加载到cache中,这样就可以降低权重数据的缺失率;
观察一下结果,我们可以了解delta输入加速效果受到哪些因素的制约。我们可以看出来rounding,加高斯噪声,使用delta数据进行训练,以及增加L1 norm都可以提高网络精度。Rounding是在量化activation中采用了rounding操作,高斯噪声是附加在x和ht上,L1 norm是对delta ht施加L1正则化。
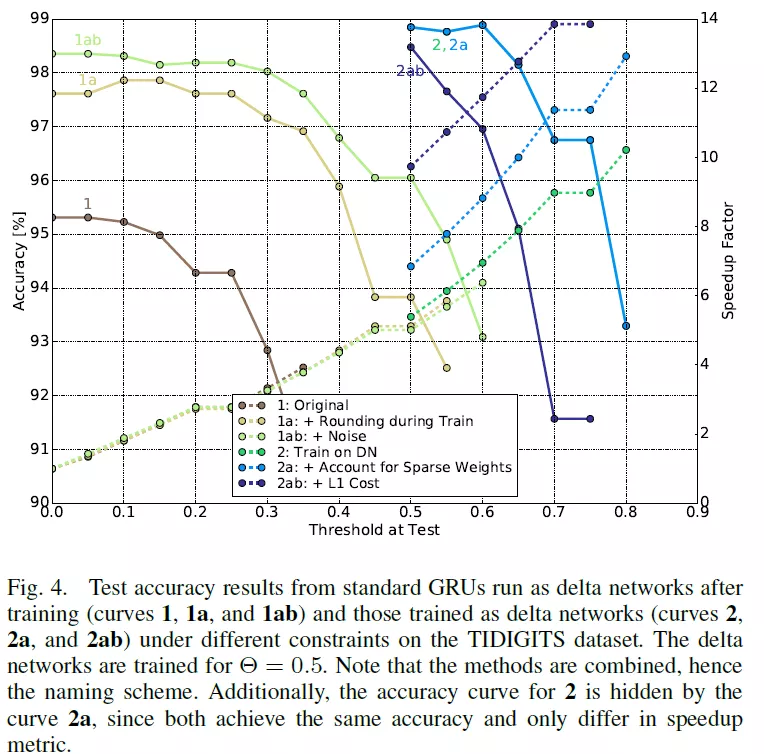
3. 量化
为了将LSTM网络成功部署到FPGA上,量化是不可缺少的步骤。免除了浮点运算的LSTM网络对FPGA才更加友好,不仅仅能够减少参数总量,还可以降低FPGA资源消耗,减轻FPGA设计难度。为了使得LSTM全部定点化,每一个operator的输入以及输出都要进行量化。常用的量化手段是统计数据的上下界范围,使用线性量化方法,将一个浮点数据表示成一个定点数和一个scale。为了硬件的进一步简化,scale可以round到2的幂次。因此最终的定点表示等效于一个具有固定小数点位置的浮点数据。当原来的浮点数据被表示为定点数据和一个bit偏移之后,硬件上对矩阵乘法,向量乘法的计算就可以通过定点数乘法和移位来实现。而对于加法操作,所有操作数的量化参数应该相同,否则不同加数之间不能够对齐小数点,就不能直接进行定点数相加,而额外的小数点对齐操作可能由于round的存在导致硬件计算结果不同于算法计算结果。比如:

非线性函数(sigmoid/tanh)用硬件实现是非常复杂的,因此对其不仅仅要做量化,还需要将非线性转化为线性计算。根据这两个函数的特点:其在一定范围是近似线性的,而超过某个范围接近饱和。有两种方法来进行处理:第一种是通过采样函数值,利用采样点近似;另外一种是使用分段线性函数来近似。
在文献[1]中,作者在函数非饱和区采样了2048个数据点作为近似值,硬件中可以通过查找表方式来计算这两个非线性函数。给定非线性函数输入后,通过移位和偏移可以将输入转化为查找表的index,然后得到非线性函数结果。查找表方式硬件实现逻辑很简单,但是会耗费一定的存储空间,特别是需要对非线性函数进行并行查找的时候,存储空间会翻倍。
在文献[5]中,作者使用了分段线性来近似sigmoid和tanh函数:
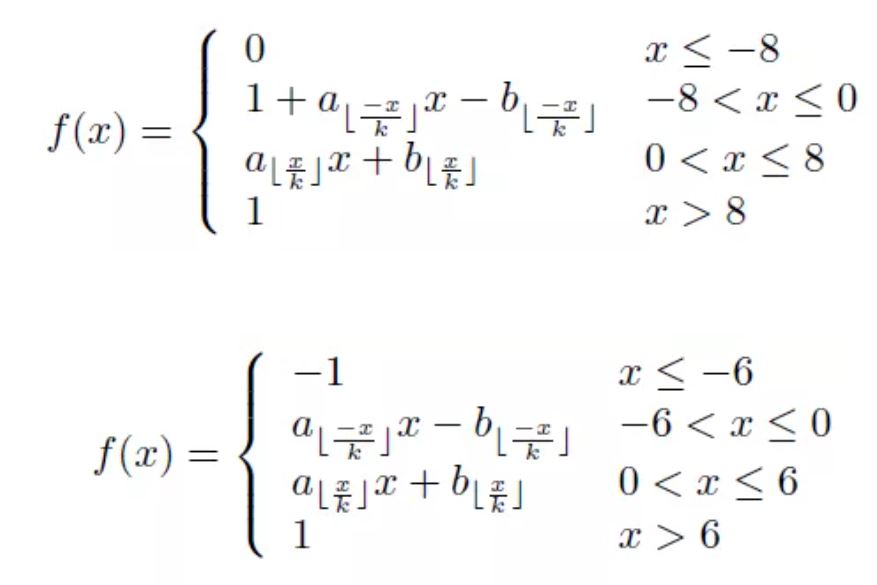
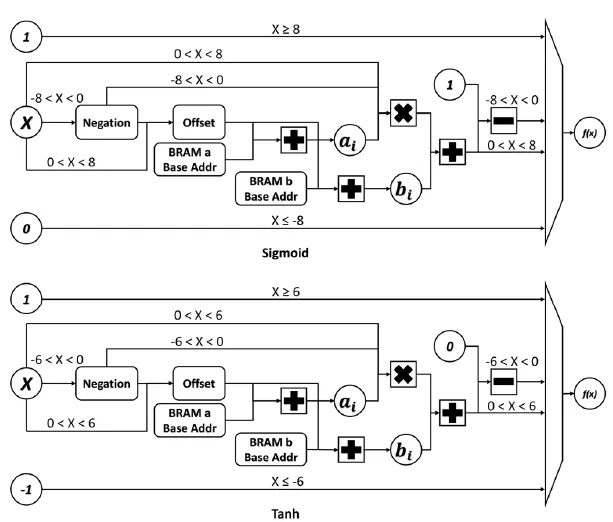
以上公式中线性区间k的大小决定了线性函数的个数,k越小,分段越多近似越好。在包河区之外用同一个值来近似饱和数值。分段线性近似需要消耗较多的组合逻辑,包括比较,mux,加法以及乘法操作。作者在文献中也给了硬件实现逻辑:线性函数的斜率a和偏移b分别保存在bram中,通过x来获得参数索引,然后得到a和b的值,在进行乘法和加法计算。
4. 硬件架构
定制化LSTM加速器基本都存在weight的稀疏化处理,因此硬件上首先要支持稀疏化数据的读取,存储和计算。根据weight稀疏化方式的不同,对有效权重数据的编码方式也不一样。在文献[1]中,作者使用了CSC(compressed Sparse Column)编码方式,即使用相对行索引和列指针来表示权重元素的位置。相对行索引即在一列权重数据中,某个数据相对上一个非零数据的偏移,相对行索引使用了4bit,而权重被压缩为12bit数据,因此权重数据和索引数据组成了16bit。这样对齐的bytes有利于数据在DDR中的存储,否则会浪费DDR存储和带宽。列指针用于表示这一列权重在原来矩阵中的位置。这样的编码方式要求硬件通过累加器计算权重数据的绝对row位置。通过row和column的位置恢复出实际的权重矩阵。

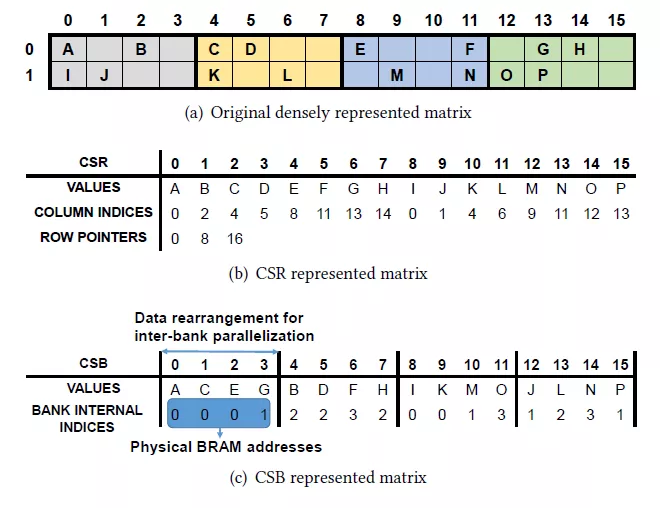
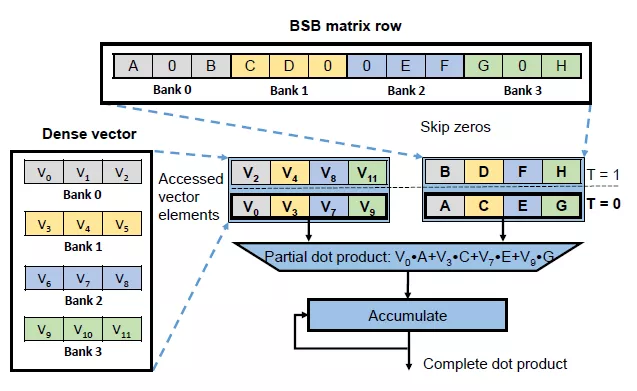
而在文献[3]中,作者根据其bank稀疏化的特性,采用了自定义的CSB编码方式。根据作者的说法,其和CSC,CSR等编码方式不同的是,可以免除硬件上解码逻辑。CSB的方式是将每一行权重中不同bank的第一个非零元素都排列在一起,然后再排列第二个非零元素……。编码采用非零元素在每个bank中的位置,这个位置可以直接作为稀疏矩阵计算单元读取权重的地址。使用bank的索引能够使用更少bit来表示,同时硬件针对其bank稀疏化进行了专门的设计,所以免除了硬件decoding。
除了以上介绍的CSC,CSB,稀疏矩阵的编码方式还有很多,比如CSR,COO等[6]。
根据LSTM的算子,硬件基本的计算单元有:矩阵乘法,非线性函数,向量加法和乘法。为了数据流在每个算子之间能够顺畅,不同算子对应硬件资源的比例应该和不同算子算力的比例相同。比如对于矩阵乘法和加法来说(假设LSTM输入为1024,输出为1024),在LSTM中矩阵乘法算力为8*2*1024*1024,加法的算力为4*2*1024+1024,那么最理想的情况是矩阵乘法使用的乘法器单元和加法器单元比例约为2048:1,即1个加法器就可以满足2048个乘法器的结果用于后续计算。即可以先计算出一个W*x和一个W*x元素,然后就可以进行二者的求和计算。如果再增加加法器,那么加法器就会有很多空闲时间。
LSTM中矩阵乘法的并行度来自于三方面:input channel,output channel以及batch方向。其中input channel对应输入的维度,output channel对应了矩阵乘法的输出维度,batch对应向量的batch数(比如对于语音信号,不同的batch为不同的输入源产生的向量)。文献[1]中是通过batch和output channel方向的并行度来提高稀疏矩阵的计算量。而在input channel方向没有并行性,这样做可以按顺序取得每一列权重中的index以及对饮的vector值,使得逻辑简化。当然也可以增加input channel方向的并行性,但是就要求每一列权重的稀疏化率相同,并且并行获取多个权重index值以及vector值。
文献[1]无法利用权重行内并行性,文献[2]中通过bank-balance的稀疏化,保证了每个bank中具有相同的非零元素,就可以同时利用权重行间和行内并行性(bank间并行性)。而且其通过将不同bank的权重排列在一起,可以在硬件上进行bank间并行计算。
定制化LSTM加速器的定制性表现在:片上存储资源针对权重,index,vector等有专用的结构,稀疏矩阵乘法是针对权重的稀疏性特点定制的结构,控制流是对LSTM计算图的映射和部分映射。这些都导致整个加速器的控制也是具有定制性。如果能够将LSTM计算图完整的映射到硬件上,可以更好的保证流水性。甚至节省了对中间结果的缓存。但是这受到FPGA资源和LSTM大小的限制。如果一个LSTM层大小为输入32输出32,那么我们可以使用8*2*32个乘法器计算矩阵乘法,即每32个乘法器计算一个结果。然后使用8个加法器,5个非线性计算单元,3个乘法器计算向量乘法。那么我们可以实现一层LSTM的完整计算流,可以在每个计算阶段耗费一个时钟周期完成。那么一个结果可以在8个周期得到,并且每个stage都可以pipeline起来。但是如果LSTM的维度更大比如1024x1024,那么FPGA可能不具有足够的乘法器资源(至少需要8*2*1024),在这种情况下,一层LSTM不能够完整的实现映射,就导致计算单元的时分复用。比如我们硬件上只有1024个乘法器资源,那么加法器,非线性单元等就存在空闲等待。因为矩阵乘法成为限制性因素,其它单元必须等待矩阵乘法完成计算。
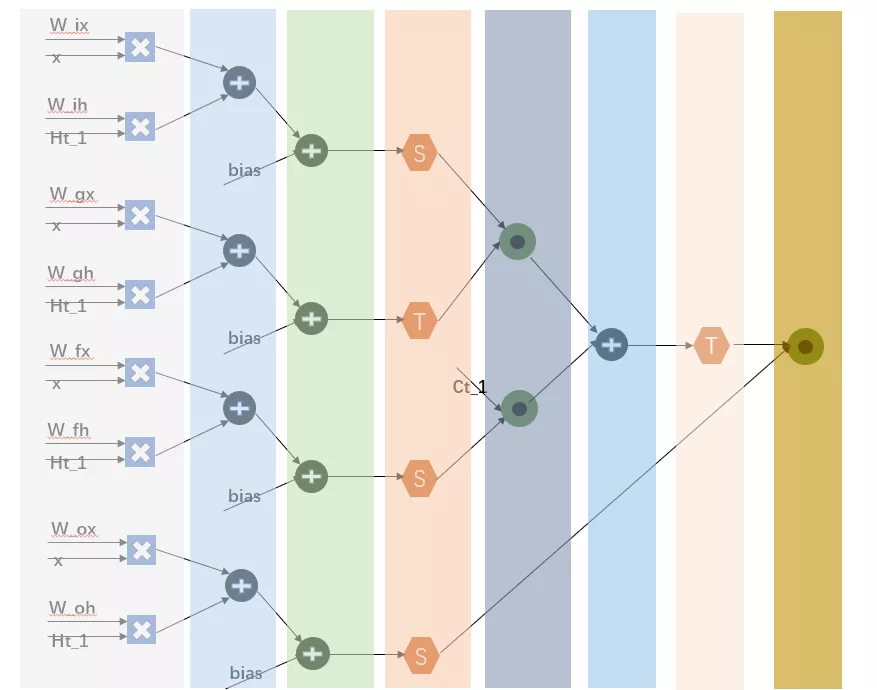
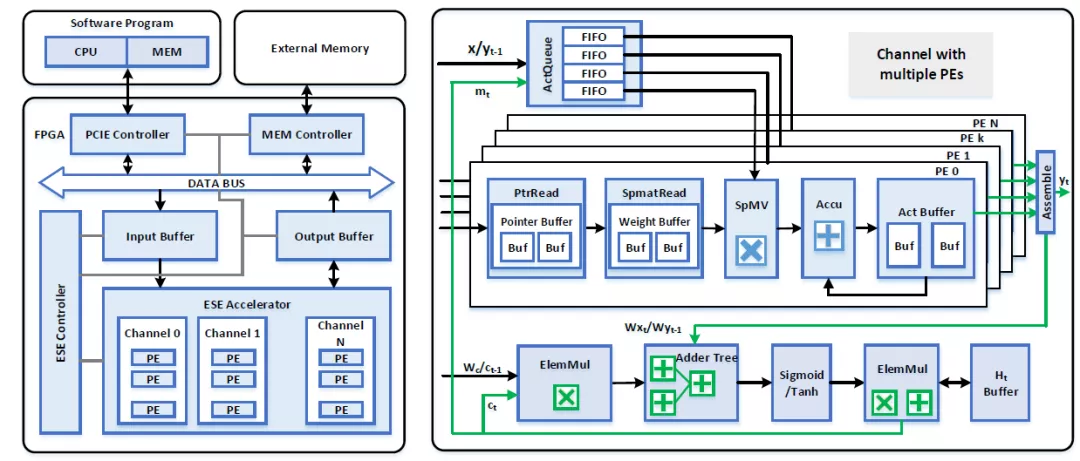
文献[1, 7, 8]中,每个算子的硬件实现都是以级联的方式进行组织的,然后控制数据流的流向。比如对于每个gate计算顺序都是:矩阵乘法->向量加法->激活函数。而ct的计算是包含element-wise乘法和加法。Ht的计算包括了激活函数和向量乘法。文献[1]中使用了更为复杂的多个算子的互联实现,分别实现了稀疏矩阵乘法,向量乘法,加法,激活函数,然后通过数据总线将其互联,然后通过控制信息来对不同的计算单元进行选择。这种方式增加了控制的复杂性,但是能够更好的复用计算单元。
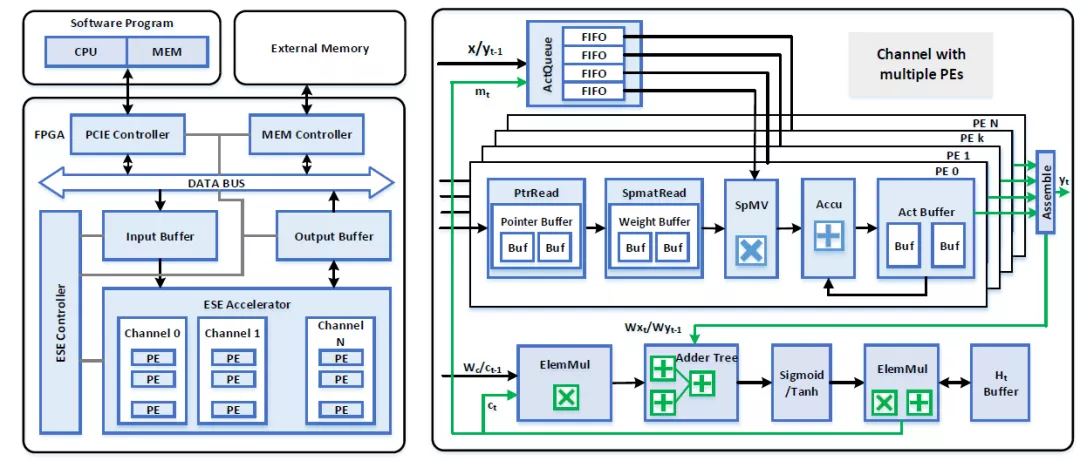
文献[8]中将gate的计算作为一个module,同时另外附加上element-wise计算(乘法和加法),这样就在一个gate上可以深度实现pipeline。其能够更好的实现gate中计算的流水,但是gate中计算单元不能够被复用。
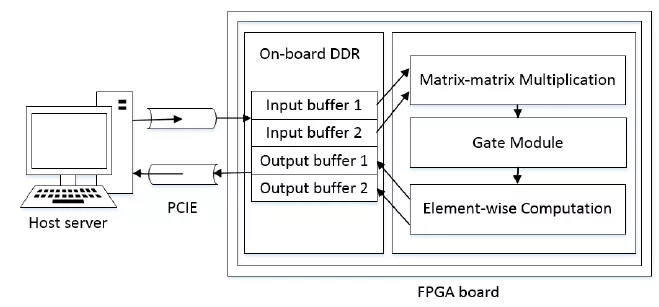
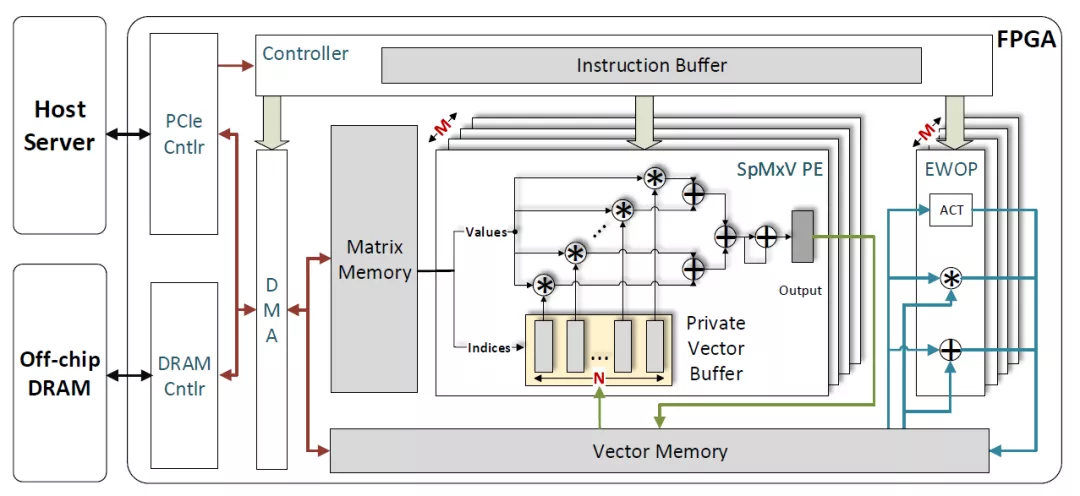
文献[2]中不同的计算单元通过buffer来实现数据交互,其稀疏矩阵乘法有单独的计算单元和权重buffer,而element-wise和激活在同一个模块中实现。矩阵计算单元和element-wise计算单元之间通过vector buffer来实现数据传输。虽然其定义了自己的指令集,但是我并不认为其是一个通用性加速器,因为其稀疏矩阵乘法单元以及matrix memory都是定制结构。定义指令集是方便编译器生成控制指令,以及软硬件具有清晰的区分。
文献
[1] ESE: Efficient Speech Recognition Engine with Sparse LSTM on FPGA
[2] Block-Sparse Recurrent Neural Networks
[3] Efficient and Effective Sparse LSTM on FPGA with Bank-Balanced Sparsity
[4] C-LSTM: Enabling Efficient LSTM using Structured Compression Techniques on FPGAs
[5] Implementation and Optimization of the Accelerator Based on FPGA Hardware for LSTM Network
[6] https://en.wikipedia.org/wiki/Sparse_matrix
[7] Implementation and Optimization of the Accelerator Based on FPGA Hardware for LSTM Network
[8] A Cloud Server Oriented FPGA Accelerator for LSTM Recurrent Neural Network