作者:Marcello Colozzo,来源:EDN电子技术设计
本文将深入分析离散傅里叶变换(DFT)和快速傅里叶变换(FFT)。
信号的采样过程是一种理想形式,因为它在时间轴上从−∞延伸到+∞,因此有无数个瞬时tn。这就破坏了使用电子计算器对采样信号进行频率分析的可能性。因此,我们需要一个能够返回有限数量的瞬时(样本)的真实采样过程。
加窗技术——频谱泄漏
从数学上讲,“截断”信号相当于将信号乘以一个时间窗口,如下所示:

相应的图表如图1所示。
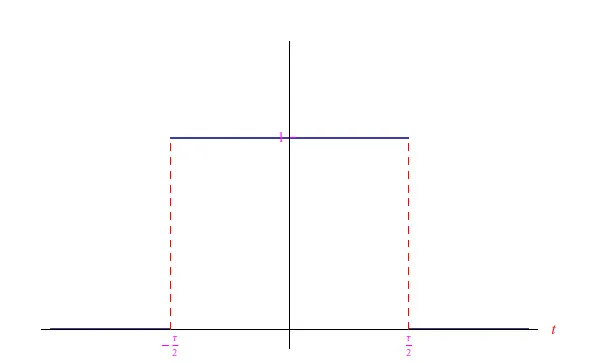
图1:时间窗口示例
由此可见,对于在整个时间轴上延伸的任何信号,对于指定的τ,截断信号由下式给出:

在计算截断信号的傅立叶变换时,卷积定理会对我们有所帮助,正如之前的教程中已经介绍过的那样。因此,我们省略了这些步骤并重点介绍截断正弦测试信号的具体示例:

傅里叶变换是下面的sinc函数:

Xτ(f)的趋势如图2所示。请注意,在τ→+∞的极限中,由于sinc函数的已知特性,通过无限增加信号的持续时间,傅里叶变换(4)将变成以f0为中心的狄拉克δ函数,因为我们现在有一个纯正弦信号,所以它一定是这样。
另一方面,对于有限的τ值,频谱分布趋于“加宽”,从而呈现出由δf=f1−f-1给出的频率色散,其中第二部分中的项是经傅立叶变换消失的第一个(对称)频率(图2)。快速计算可得δf=2/τ。频率色散(被称为频谱泄漏)表示由于采样而导致混叠的信号进一步失真。可以通过增加时间窗口的持续时间或使用非矩形窗口(平滑窗口)来减少这种失真。

图2:截断的信号频谱(3)
离散傅里叶变换
无论是在采样信号xc(t)的情况下,还是在截断和采样信号xτ,c(t)的情况下,频率都从-∞到+∞连续变化并且可以被离散化。由此产生的算法让我们能将时域tn=nTc转换为频域fn,缩写为DFT:离散傅立叶变换。抛开下标τ,c不看,假定样本序列{xn:n=1,…,N}为周期性的,周期为τ=NTc,即频率由下式给出:

频域采样遵循f→fn=kfτ:

其中我们考虑到了方程(5)。结果是:

此处,Xh=X(fh),其中h=0,1,…,N−1。复数序列Xh定义了xτ,c(t)的DFT。更准确地说,复数Xh被称为h的频谱分量。在连续情况下,傅立叶变换Xτ,c(f)的量纲为x(t)除以频率,因为Xτ,c(f)是频谱密度(每单位频率间隔内频谱分量的幅度)。
然而,在离散情况下, Xh与x具有相同的量纲,因为Xh不是频谱密度而是分量的幅度。将方程(7)反转:

以对称形式,我们有:

提供频率分布信息的频谱分量是k=0,1,..,N/2的频谱分量。由式(6)我们可以得出:

频率由下式给出:

这就是所谓的折叠频率。让我们将这些概念应用到下面的调幅正弦信号的研究中:
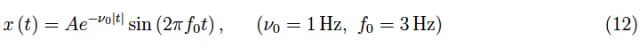
如图3所示,指数衰减让我们能用持续时间τ=4秒的窗口截断信号。我们使用Tc=10−2s进行采样,因此fc=10Hz。通过使用Mathematica执行傅里叶变换,我们可以得到相应频谱的图表(图4),其中横坐标出现的是样本,而不是频率。为了使后者出现,我们必须使用方程(6)。
图3:信号被截断(12)

图4:截断和采样信号的傅里叶频谱(12)
通过向Mathematica发送正确的指令(通过列表),我们获得了频谱与频率的函数关系,如图5所示。但是,它仍然不是很清楚。让我们尝试缩小范围,获得如图6所示的频谱。从中,我们可以看到3Hz左右的峰值,这正是正弦波振荡的频率(ν0控制调制包络的宽度,因此尽管它具有过去倒数的量纲,却不是频率)。回到图5,我们可以看到折叠频率为50Hz,从这一频率开始,频谱就是之前频谱的翻版。我们可以得出结论,所研究信号的傅里叶频谱仅在3Hz附近才与零点有明显不同,因此3Hz是主频。
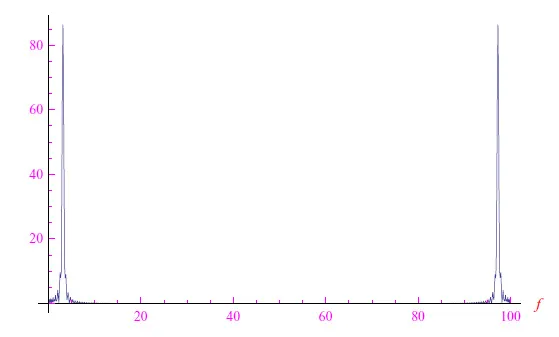
图5:截断和采样信号的傅立叶频谱与频率的函数关系
快速傅立叶变换
方程(9)可以写成矩阵形式。准确地说,是N阶方阵的行乘列与N行列向量的乘积。因此,DFT的计算需要N2量级的多次运算。由此我们可以理解,当样本数量较多时,这种算法的计算成本会很高。为了减轻计算负担,人们开发了各种以FFT为缩写的算法,将运算次数减少到O(N ln N)。
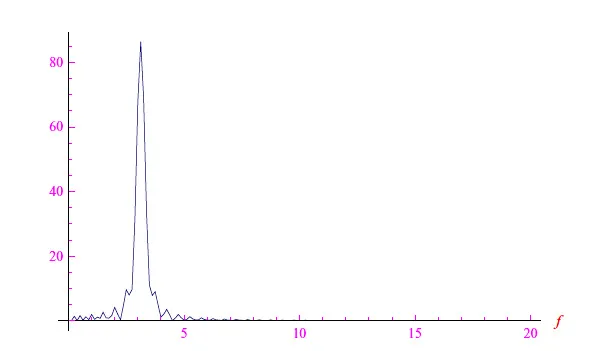
图6:就是上图的傅立叶频谱,但频率范围缩小了