快速傅里叶变换（FFT）：从数学公式到5G信号，揭开数字世界的“频率密码”
judy 在 周四, 02/20/2025 - 09:38 提交
你是否想过，为什么手机能瞬间解码WiFi信号？为什么音乐APP能一键分离人声和伴奏？答案就藏在快速傅里叶变换（FFT）这个“数字魔法”中
傅里叶变换
线性联合时频分析方法中的短时傅里叶变换：STFT
judy 在 周三, 01/10/2024 - 09:39 提交
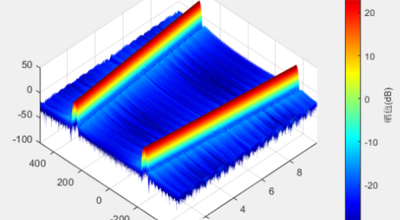
本文用Matlab仿真一个简单的线性调频信号，参数设置如下：
深入分析：离散傅里叶变换(DFT)和快速傅里叶变换(FFT)
judy 在 周三, 12/20/2023 - 10:11 提交
本文将深入分析离散傅里叶变换(DFT)和快速傅里叶变换(FFT)。
傅里叶级数→傅里叶变换
judy 在 周四, 10/19/2023 - 09:39 提交
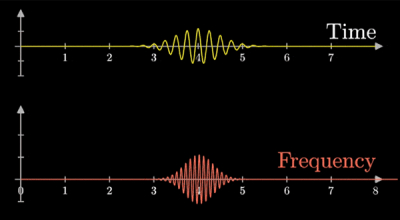
傅里叶变换实际上就是对一个周期无限大的函数进行处理
雷达信号处理 | 快速傅里叶变换(FFT)中的增益损失
judy 在 周三, 07/26/2023 - 10:07 提交
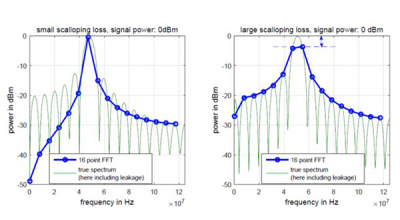
本文主要解释如何用FFT精确地测量信号功率（signal power）
傅里叶变换、拉氏变换、z变换的含义
judy 在 周二, 07/18/2023 - 09:31 提交
fourier变换是将连续的时间域信号转变到频率域
深入浅出的学习傅里叶变换
judy 在 周五, 01/06/2023 - 10:31 提交
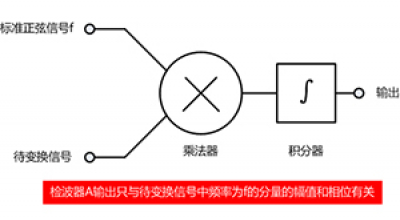
学习傅里叶变换需要面对大量的数学公式，数学功底较差的同学听到傅里叶变换就头疼
通俗讲解：傅立叶分析和小波分析之间的关系
judy 在 周一, 02/21/2022 - 14:51 提交
从傅里叶变换到小波变换，并不是一个抽象的东西，完全可以讲得很形象。小波变换有着明确的物理意义，如果我们从它的提出时所面对的问题看起，可以整理出非常清晰的思路
【下载】在AI引擎上实现逐块可配置的快速傅里叶变换应用说明
judy 在 周五, 01/15/2021 - 15:46 提交
快速傅立叶变换(FFT)已被广泛应用于各种信号处理算法中，这些算法通常需要可配置FFT大小的高吞吐量。本应用说明展示了在Xilinx® Versal™ AI Core器件中的AI Engine (AIE)阵列上高效的FFT实现。
Matlab中短时傅里叶变换 spectrogram和stft的用法
judy 在 周二, 05/26/2020 - 10:56 提交
在Matlab中，做短时傅里叶变换需要使用函数spectrogram，而在Matlab2019中，引入了一个新的函数stft，下面我们就来看下这两个函数都如何使用。