DSP基础
3.3时域和频域
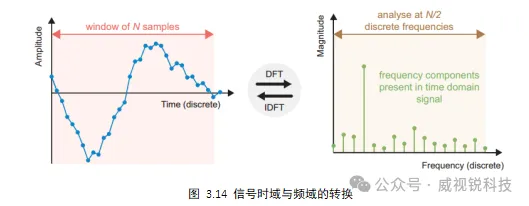
从时域到频域的转换的简单描述如图3.14所示。离散傅里叶变换(DFT)通常以更有效的形式实现为快速傅里叶变换(FFT),用于执行转换。逆DFT(IDFT)或逆FFT(IFFT)可用于进行从频域到时域的相反转变。
3.4 定点算法
硬件设计中主要使用两种定点数:无符号数和二进制补码。在这两种情况下,数字都由整数位和小数位组成,由一个二进制点分隔。通常以(s,n+b,b)的形式指定格式,其中s表示格式(0为无符号,1为有符号的二进制补码)。例如,(0,8,5)表示一个具有3个整数和5个小数位数的无符号数。
3.4.1 无符号定点格式
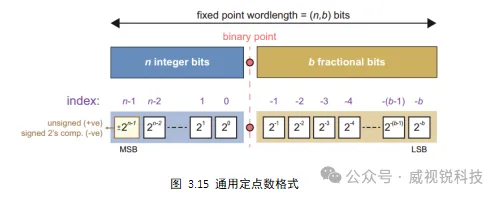
无符号定点格式适用于信号只能取非复负值的情况,例如用于控制电路的计数器。无符号定点数由整数位和小数位组成,由一个二进制点分隔。形成数字的比特从左边的最高有效位(MSB)排列到右边的最低有效位(LSB),并且每个比特都具有单独的比特权重。图3.16描述了一个通用定点数的结构。
3.4.2 二进制补码格式
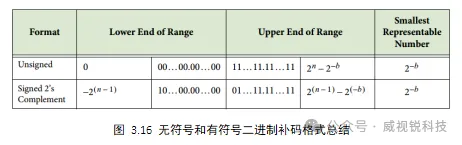
二进制补码格式与无符号格式相似,不同之处在于MSB具有负加权,如图3.15所示。因此二进制补码可以表示负数。MSB为0 时代表正数,为1时代表负数。图3.16总结了两种固定点格式的范围和精度。
3.4.3 字长增长
当不动点是算术运算的对象时,通常应该允许它们增长,以避免溢出。然而,较长的字长会导致运算电路的实现成本更高。作为一个简单的经验法则,当两个数字相加或相减时,该数字的整数部分应增加1位。这将使可用范围翻倍,并确保所有可能的答案都能表示出来。乘法运算会导致更大的幅度变化。为了避免上溢和下溢,应该将两个被乘数的整数部分和小数部分相加。
3.5 滤波
3.5.1 滤波器响应类型
当希望以某种方式改变信号的频率内容时,例如去除某个频带时,通常对信号进行滤波。滤波器可分为四种响应类型,即:低通、高通、带通和带阻,如图3.17所示。
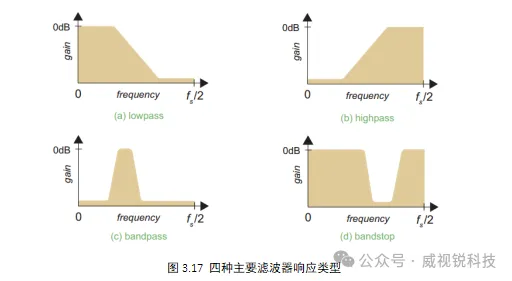
还有一类滤波器是全通滤波器,在这里不重点讨论。信号的幅度不会通过滤波而改变,相反,滤波的目的是修改信号的相位。
3.5.2 滤波器幅值响应特征
滤波器可以在模拟域和数字域中实现,滤波器响应可以用一组关键特征来描述。图3.18以低通滤波器响应为例说明了这些滤波器特性。在这里定义了响应的三个区域:通带、过渡带和阻带。通带中的信号频率分量经历大约0dB的增益。在阻带中,信号受到衰减。在通带和阻带之间存在具有滑动增益的过渡带。
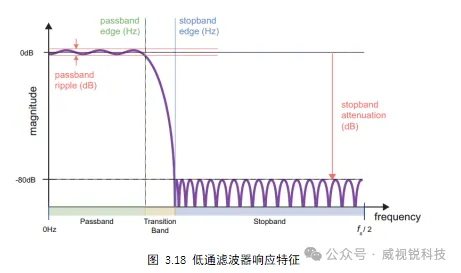
在指定滤波器的要求时,通常使用以下参数:通带频率、阻带频率、通带波纹和阻带衰减。过渡带宽对应于通带和阻带边缘频率之间的差。理想的滤波器响应通带增益为0dB,阻带衰减无限,过渡带宽为0Hz,如图3.19所示。
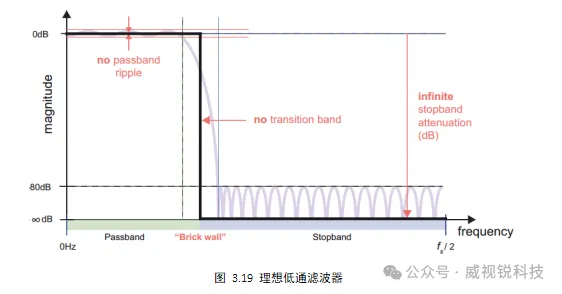
对于带阻滤波器和带通滤波器,分别有两个通带区域和两个阻带区域,并且可以单独设置响应的这些附加特征的参数。例如,带通滤波器的两个阻带区域中的衰减不需要相等。
3.5.3 无限和有限脉冲响应滤波器
要进行的基本设计选择之一是选择有限脉冲响应(FIR)或无限脉冲响应(IIR)滤波器。顾名思义,FIR对脉冲的响应仅持续有限数量的样本。相比之下,IIR滤波器对脉冲的响应在理论上可以永远持续。图3.20中提供了比较两种滤波器响应类型的示意图。
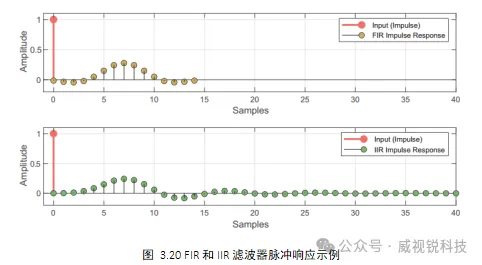
FIR滤波器对数据样本窗口执行加权平均(卷积),如(3.10)。
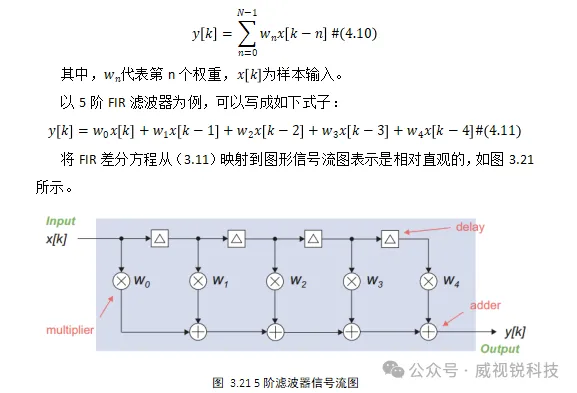
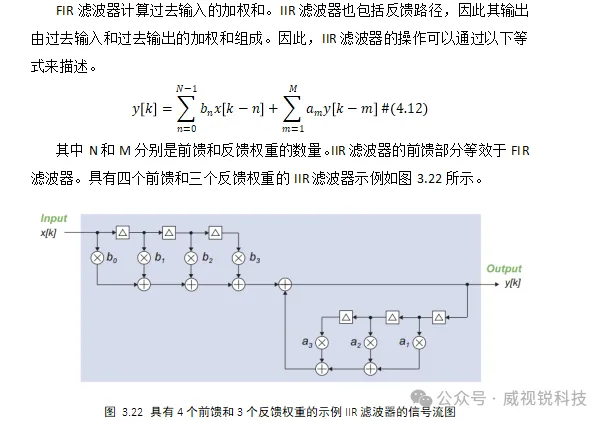
选择IIR滤波器的主要动机是,它们可以使用更少的权重来实现与FIR滤波器相同的幅度响应,因此它们需要更少的计算,并且在硬件中实现的成本更低。然而,FIR滤波器具有两个有利的特性,这使它们成为通信应用的首选:FIR滤波器本质上是稳定的,因为它们没有反馈路径;任何由标准算法之一设计的FIR滤波器都具有对称的权重,因此具有线性相位响应的属性。这意味着通过滤波器的所有频率都被延迟相同的时间量,这对应于线性增加的相位差。
线性相位响应属性的意义在于保持不同频率分量之间的相位关系,这在通信中尤为重要,因为通信中信息由由几个不同频率组成的“脉冲”携带。脉冲形状可以被非线性相位滤波器破坏,但被线性相位滤波器保留。
3.5.4 z域滤波器响应
数字滤波器和其他DSP算法通常使用z域表示进行描述,z域表示提供了一种方便且数学上易于处理的形式。
因果信号的单侧z变换可以定义为:
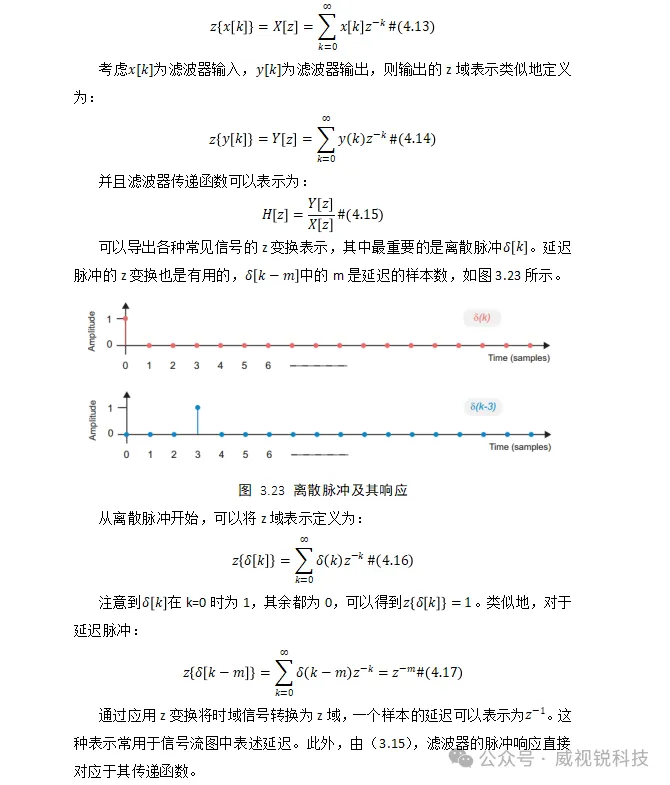
3.5.5 数字滤波器设计
滤波器响应的期望特性表示对设计过程的输入。例如,为了设计低通滤波器,通常提供通带边缘频率、阻带边缘频率、通带纹波和阻带衰减的参数。滤波器设计算法然后试图满足这些要求,并假设它可以做到这一点,输出一组实现所需响应的滤波器权重。通常,除非被约束为生成特定长度的滤波器,否则设计算法输出一个滤波器,该滤波器以最小数量的权重实现所需的响应,因为这代表了计算效率最高的解决方案。
滤波器设计有几种不同的方法,包括FIR滤波器的窗函数法、频率采样法、最小二乘法和Parks-Mclellan(Equiripple)方法。对于任何给定的输入参数集,每种方法都可能产生略有不同的响应。
3.5.6 FIR滤波器的实现
在设计了滤波器响应并生成了实现滤波器所需的权重集后,下一步是实现它。在使用RFSoC平台的通信设计中,自然目标资源是PL。PL提供了一种灵活、高度并行和低功率的选择,并且能够支持通信系统中经常需要的高采样率。因此,我们将重点讨论FIR滤波器的基于PL的实现。
以11权重对称FIR滤波器为例,我们通过预加来自输入延迟线的和以相同权重值相乘的样本来利用对称性。这将实现滤波器所需的乘法器总数减少了大约一半,高效对称结构如图3.24所示。
滤波器中的基本计算单元是乘法累加(MAC),并且实现MAC所需的硬件被称为MAC单元。PL被优化用于实现FIR滤波器结构,并且它的每个DSP48E2片可以支持一个MAC单元,该MAC单元包括权重乘法器和后加法器,以及前加法器和所有相关联的延迟元件。因此,这个11权重的例子可以使用六个DSP48E2片来实现,而不需要任何额外的PL逻辑。

此外,值得注意的是,上面讨论的实现是完全并行的,其中信号流图中的每个乘法器(例如)对应于PL中的物理硬件乘法器。因此,实现滤波器所需的硬件量在滤波器权重的数量内。另一种可能性是串行化或部分串行化滤波器实现,以减少其资源占用——这是通过分时MAC单元实现的,因此每个MAC单元为滤波器的每次执行计算两个或多个MAC操作。只有当滤波器硬件的运行速度至少是要支持的采样率的两倍时,这才有可能实现,因此它不适合以非常高的采样率进行处理,但对于以较低的采样率运行的滤波器实现来说,它可能是一个非常有用的工具。
3.5.7 滤波器设计权衡
通常,以下设计选择往往会增加实现滤波器所需的权重数量:
1. 减少允许的通带波纹量
2. 增加所需的阻带衰减
3. 指定通带和阻带之间较窄的过渡带
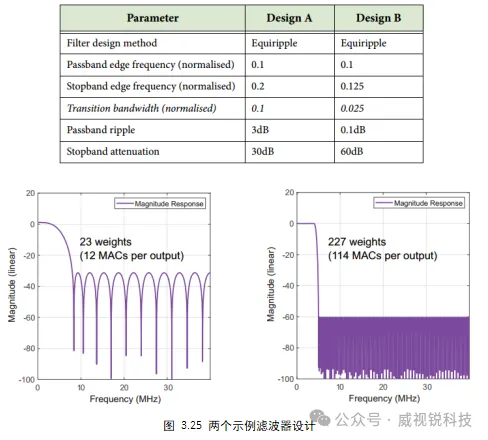
例如,如果要将转换带宽减少两倍,这将使所需的滤波器权重数量增加一倍左右。图3.25中给出了两个示例低通滤波器设计的设计参数以及由此产生的滤波器设计。
图中右侧滤波器的响应更好但其所需计算量为左侧的十倍,意味着所需资源和功耗的增加。滤波器的性能与实现它所需的计算和处理硬件之间存在权衡。一种谨慎的方法是设计每个滤波器,以最大限度地减少权重和固定点字长的数量,同时仍能达到所需的功能规范。
文章来源:威视锐科技