DSP基础
3.6 模拟-数字接口
3.6.1 模数转换
如前所述,可以通过对信号进行采样和量化来将连续时间模拟信号转换为数字等效信号,与这些操作相关的关键参数是采样率和量化器中使用的量化位数。
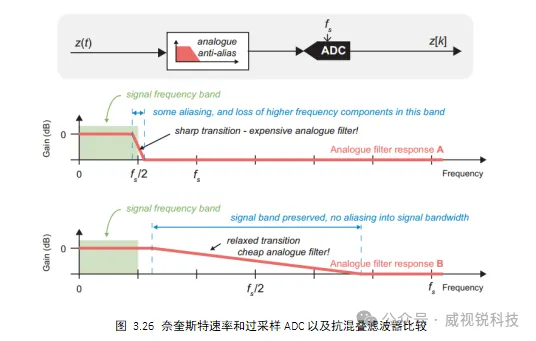
由于实际设计中,理想滤波器无法实现,因此可以使抗混叠滤波器在奈奎斯特一区的上限以下截止,其后果是丢失了一些感兴趣的频率分量;也可以使过渡带稍微延伸到奈奎斯特二区,这意味着可能会出现某种程度的混叠。上述突出的问题可以通过ADC处的过采样来解决,即,根据奈奎斯特采样定理,以比其必要的更高的速率进行采样。因此,可以使用更宽松的模拟抗混叠滤波器,其实现成本更低。任何混叠分量都不会影响感兴趣的频带,并且可以在ADC之后使用数字滤波器去除。这两种不同方法之间的比较如图3.26所示。
过采样方法的一个可能的缺点是,在数字域的输入处采样率高于所需的采样率,这意味着后续处理阶段的计算负载更高。通过在ADC之后不久使用多速率滤波器来降低采样率,使得以更接近奈奎斯特速率的速率对信号进行采样,可以容易地解决该问题。
3.6.2 数模转换
传统的数模转换过程包括从离散样本和振幅再生连续时间信号,这通常是使用零阶保持技术来完成的,该技术会产生如图3.27所示的“阶跃”信号。
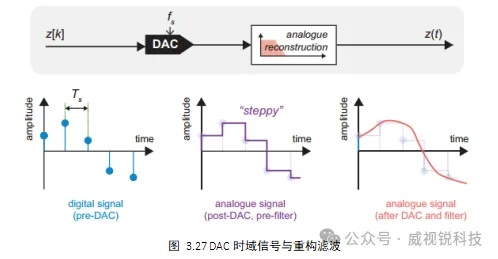
DAC输出的信号,包括感兴趣的信号以及图像频谱,遵循矩形滤波器响应的正弦形状,如图3.27所示。DAC响应的轮廓意味着频谱图像仅被部分衰减,留下具有显著能量的残余,需要通过模拟重建滤波器进一步衰减。这起到衰减奈奎斯特区上部存在的重要频率分量的作用,并在这样做的过程中平滑时域信号,以产生更直观的“模拟”波形。这种重建滤波器的应用可能会使感兴趣的信号带失真。过采样技术可以一定程度上解决这些问题,此外,也可以在DAC之前,在数字域中引入反向sinc滤波器校正其响应。
3.6.3 更高奈奎斯特区
RFSoC设备中的一个重要创新是RF-ADC和RF-DAC能够在上部奈奎斯特区外操作。在ADC或DAC工作在更高奈奎斯特区的情况下,本节中讨论的模拟滤波器不应再是低通滤波器,而是必须设计为针对所需频率范围的带通滤波器。
3.7多速率操作
3.7.1 多速率处理的动机
多速率处理通常用于保持大于奈奎斯特速率的采样率,定义如下
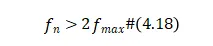
在信号带宽发生变化的情况下,可能希望使用多速率技术来增加或减少采样率,从而保持采样率和信号带宽之间的类似关系。应用的示例包括:匹配将被组合的两个信号路径的采样率、信号带宽变化时调整采样率、匹配外部接口的采样率、简化模拟抗混叠或图像抑制滤波器的要求。
3.7.2 过采样ADC和DAC
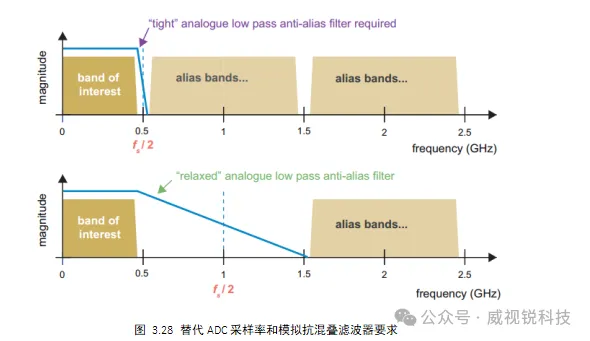
以模数转换为例,如果信号占用0 MHz和480 MHz之间的频率,并且ADC在1 GHz的采样频率下工作,则520 MHz和1 GHz之间的频带将别名为感兴趣的频带,如图3.28的上部所示。因此,需要一个具有非常紧密过渡带(在480MHz和520MHz之间截止)的模拟抗混叠滤波器——这样的滤波器设计可能很难实现,而且成本很高。
作为一种替代方案,采用2 GHz的ADC采样率将允许更宽松的模拟抗混叠滤波器响应,如图3.28的下半部分所示。可以在ADC之后引入多速率操作(抽取2),以将采样率降低到1 GHz,并以数字方式执行抗混叠任务的剩余部分。
在DAC,类似的原理适用于过采样和模拟滤波要求。在DAC处引入过采样可用于减少对模拟镜像抑制滤波器的要求。较高的采样率是通过DAC之前的插值来实现的。
3.7.3 抽取
抽取是降低采样率的过程。在最简单和最常见的情况下,这是通过整数因子来实现的,该整数因子通常表示为M。抽取包括两个过程:抗混叠低通滤波和下采样,如图3.29所示。
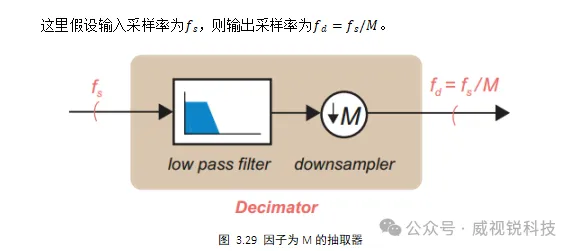
低通滤波用于去除会产生混叠的频率分量,降采样通过只保留第M个样本来降低采样率。抽取过程的时域与频域变化如图3.30所示。在频域中,由于降采样,频谱分量移动得更加靠近。由于之前已经通过低通滤波,所以不会出现混叠。
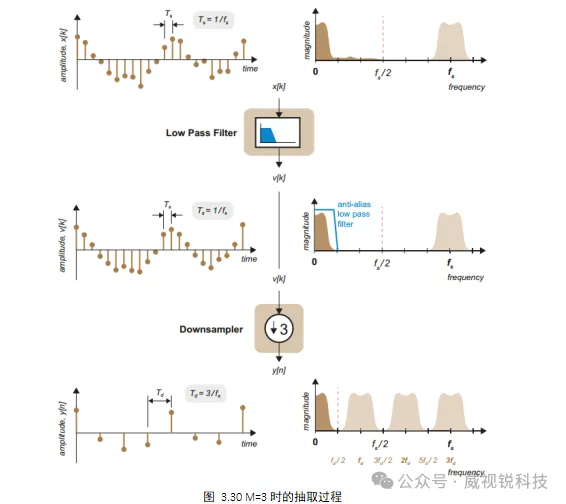
在实现方面,图3.30所示方法直观但会浪费计算,且冗余计算的比例随抽取率的增加而增加。解决这一方法通常以多相形式来实现。
3.7.4 插值
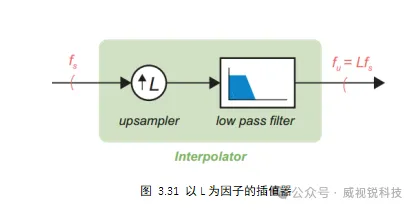
插值会增加采样率,通常通过表示为L的整数因子来增加采样率。插值器由升采样操作和低通滤波器组成,如图3.31所示。升采样在原始样本点之间插入零值从而提高采样率。
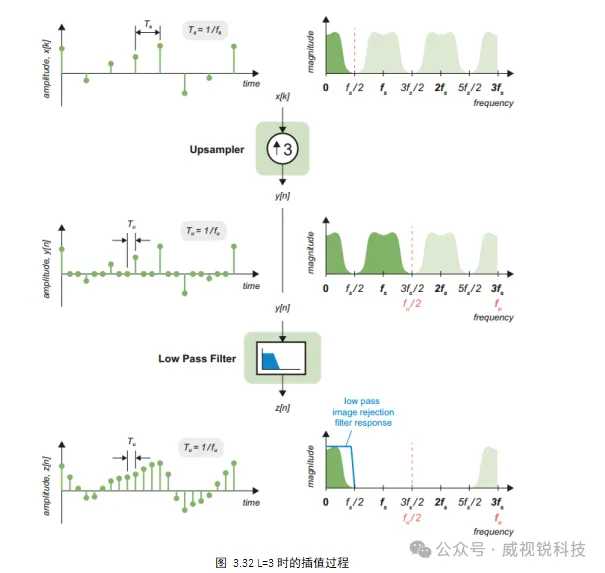
插值过程在时域与频域中的变化如图3.32所示。
在频域中,以原始采样率对称的两个频谱分量存在于0Hz到新的升采样采样率一半之间的区域中。必须使用低通滤波器来去除这两个频谱分量,这在时域中表现为信号的“平滑”,即零值样本被插值到原始样本之间的中间振幅。插值滤波过程中插入的零值样本造成了一定程度的冗余计算,且插值率越高,冗余计算越多。
对于插值和抽取,都可以使用多相方法来实现,它所需计算量小得多,且结果与直接方法相同。多相插值器和抽取器适用于PL中的实现,并且实际上可以利用减少的计算需求来产生非常节省资源的设计。
3.7.5 半带和L波段滤波器
以整数因子R变化速率时,需要一个带通滤波器通过第1/R个频带。奈奎斯特滤波器也成为L波段滤波器,满足通过第1/R个频带,如图3.33所示。
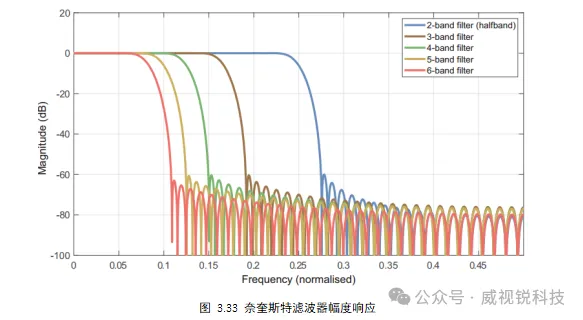
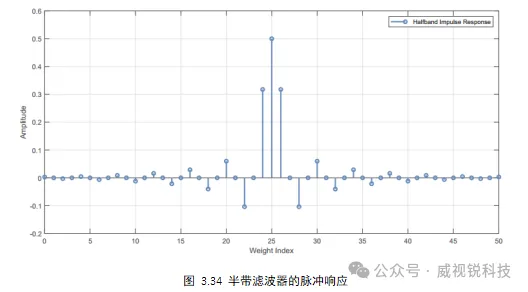
如图3.34所示,半带滤波器的脉冲响应是对称的.
3.7.6 抽取和插值级联
当抽取或插值任务扩展到更大的整数因子时,需要阶数更高的滤波器以及更多的计算。因此通常将较大的变化率因子划分为几个较小的变化率任务,可以使得滤波器设计更简单,总体计算量更小。
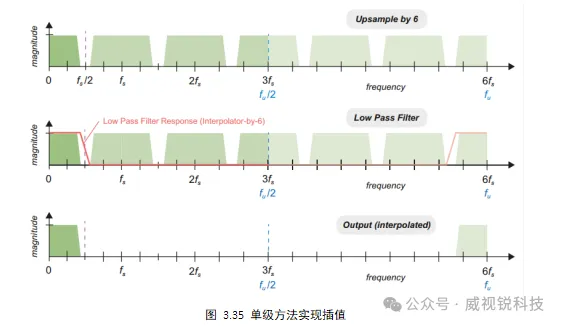
举一个简单的例子,考虑一个占据0到45MHz频段的信号,该信号将被6倍的插值。
加速允许0.2dB的通带纹波,并且阻带衰减至少为60dB。假设采用插值器实现的直接方法。单级方法要求151阶的对称滤波器来满足,该滤波器工作在600MHz,因此计算速率为45.6gman/s,插值过程如图3.35所示。
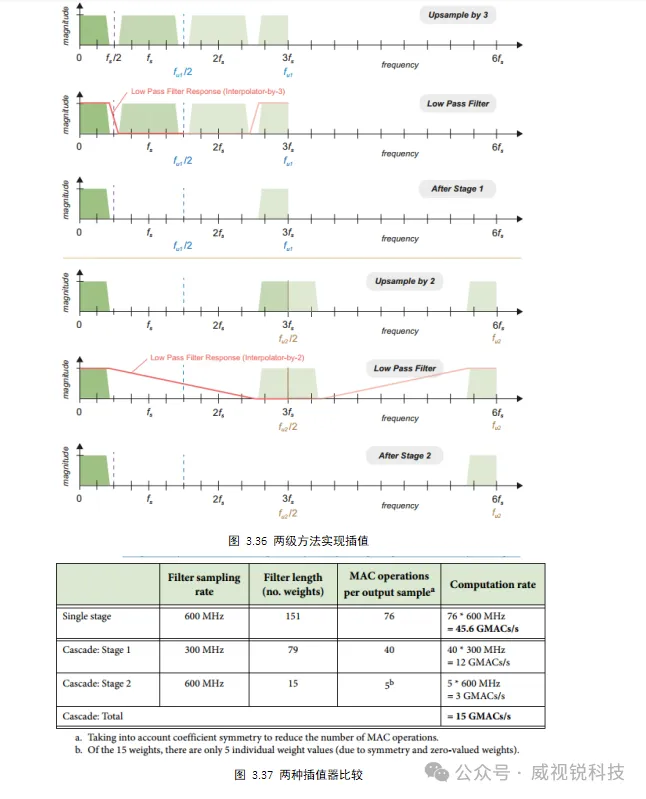
采用两级实现,使单个速率变化分别为2和3,这两个阶段分别示意在图3.36的上半部分和下半部分。在第一阶段中,产生了很大一部分空的频谱,因此第二阶段滤波器的过渡带可以更宽,从45MHz扩展到了255MHz,从而实现更简单的滤波器设计。
在前述参数情况下,将二者的计算过程进行比较,如图3.37所示。级联设计在计算方面节省了相当大的成本。
这个例子表明,与单级插值器相比,级联插值器可以减少计算需求。在可能的情况下可以选择尽量小的速率变化因子,并最大限度地使用因子为2的抽取器和插值器,其中可以利用半带滤波器的效率。
3.7.7 积分梳状(CIC)滤波器
积分梳状滤波器是一种特别有效的滤波器,通常用于多速率操作。CIC由多个级联的积分器和梳状滤波器(非常简单的无乘法器滤波器)组成。从移动平均线派生出单个阶段,即长度为W权重的FIR滤波器,其中每个权重值为1/W。CIC的诀窍是重新制定移动平均线的计算,这样就代替了传统的FIR结构,可以使用降低复杂性的架构来实现相同的输出。
但CIC在幅度响应方面不够好,通带仅在非常低的频率下平坦,而阻带衰减仅在几个级联时才较可接受。CIC滤波器在多速率系统中经常负责插值的最后阶段或抽取的第一阶段,此时采样率最高,计算效率最高。
3.7.8 重采样和其他多速率操作
除了简单的以整数因子进行抽取和插值之外,主要还有三种操作需要注意。第一种是用有理数对信号进行重采样,合理的分数速率变化可以使用插值器和十进制器的级联来实现。第二种是通过无理数或随时间变化的因子对信号进行重采样,当重采样比没有方便的基于整数的表达式或者是动态时,就需要不同类型的方法来实现,常用的方法包括高度过采样多相滤波器和Farrow结构。第三种为改变采样相位,或引入分数延迟,有时可能希望将信号延迟的持续时间小于一个采样周期,这可以使用与第二类相似的方法来实现。
文章来源:威视锐科技