傅里叶变换实际上就是对一个周期无限大的函数进行处理,将一个时域非周期的连续信号,转化为一个在频域非周期的连续信号,从这个方面来说傅里叶变换可以处理周期和非周期信号
傅里叶级数处理周期信号
傅里叶变换处理周期和非周期信号

生活中遇到的很多事情都是非周期的,比如将我们的生命比作一个沿时间不断变化的函数,有高潮有低谷,但是添加上傅里叶变换以后可以看作各种正弦波或者圆环不断叠加、交织组成每个人的生活。那么处理非周期的信号就尤为重要。所以有傅里叶级数还不够,我们需要一个数学工具来处理非周期信号,这就是傅里叶变换。
关于傅里叶级数可以查看前期内容:傅里叶级数的来龙去脉
如何通过傅里叶级数得到傅里叶变换呢?统共分三步
1、把傅里叶级数用复数形式表示(此处用到欧拉公式)
2、把傅里叶级数中的周期T变成∞(无穷大)
3、对数学公式进行简化
实际上我们在讨论傅里叶级数的时候已经悄悄用到了周期函数的傅里叶展开:
推导过程,可以看高等数学的书,此处暂时不展开。
其中几个前置知识要搞清楚:
1、什么叫正交性
2、三角函数的正交性

但这和我们平常看到的不太一样,是的,结合欧拉公式我们就会得到另一个形式

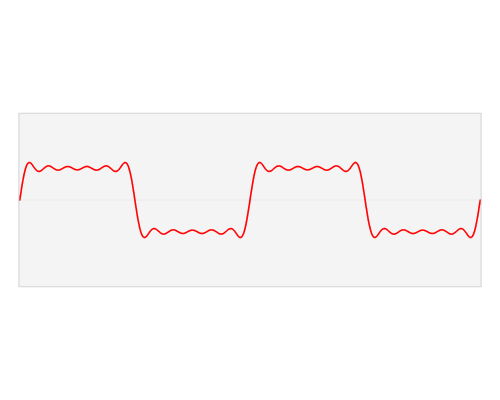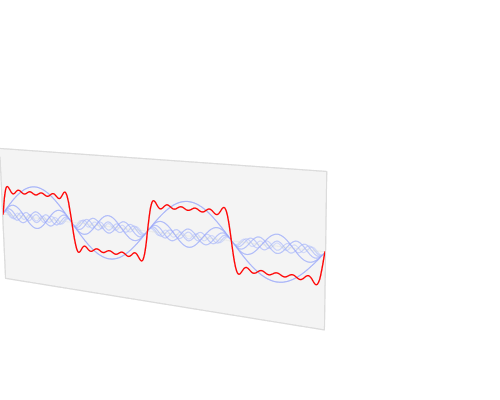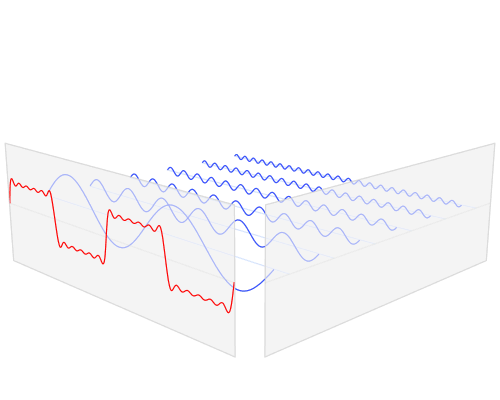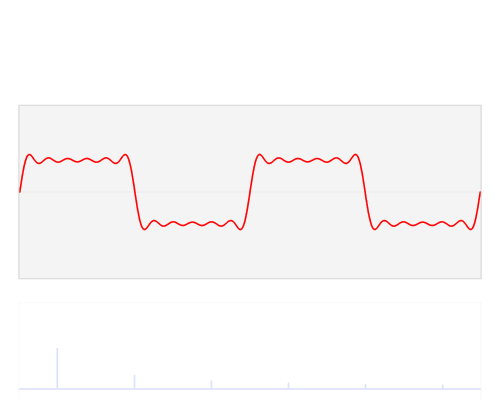
通过欧拉公式,我们把傅里叶级数中三角函数用复数来表示了。


所以,利用欧拉公式,我们可以得到傅里叶级数的复数形式:
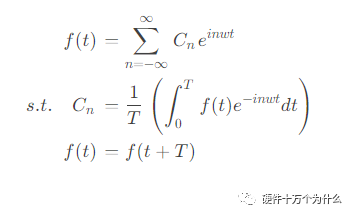

频率和周期的关系
我们有了傅里叶级数的复数形式,目的就是为了去解决非周期函数的问题。
非周期函数到底怎么能把傅里叶级数运用起来呢?
我们看到傅里叶级数的复数形式,我们看到了积分的范围是一个周期。同时,也知道频率和周期的关系。
将非周期函数由时域转换为频域的变换即为傅里叶变换。非周期函数可以看作 T → ∞ ,因此

为了方便计算,我们把积分的周期从0~T,改一下,也是一个周期,积分区间取为-T/2~T/2,则,傅里叶复数形式:
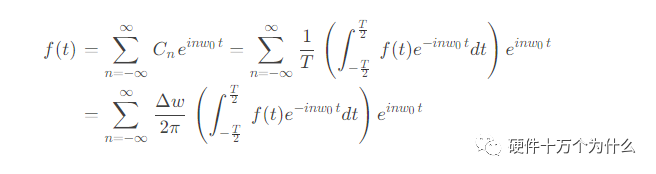
我们把T变成无穷大,


代入傅里叶级数的复数形式可得
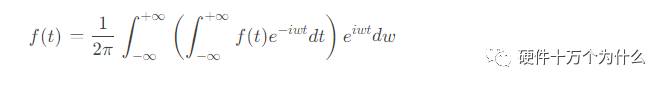
傅里叶变换即为中间括号里的积分项:
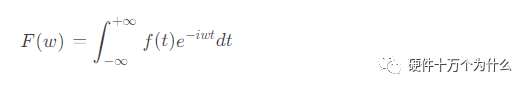
傅里叶变换的逆变换即为:

本文整理自
1、《信号与系统》奥本海姆
2、傅里叶级数、傅里叶变换 (FT) CSDN博客连理o
本文转载自:硬件十万个为什么