文章来源：FPGA入门到精通
在数字信号处理中，滤波器应用非常广泛，包括信号的过滤、检测和预测等等。
滤波器在数据采集和分析中有多种应用。它们用于通过降低或放大某些频率来改变时间信号的频率内容。
例如，如图1所示，低通滤波器以三种不同的方式影响信号中的频率内容：一些频率内容保持不变，而其他频率内容要么幅度减小，要么完全从信号中去除。
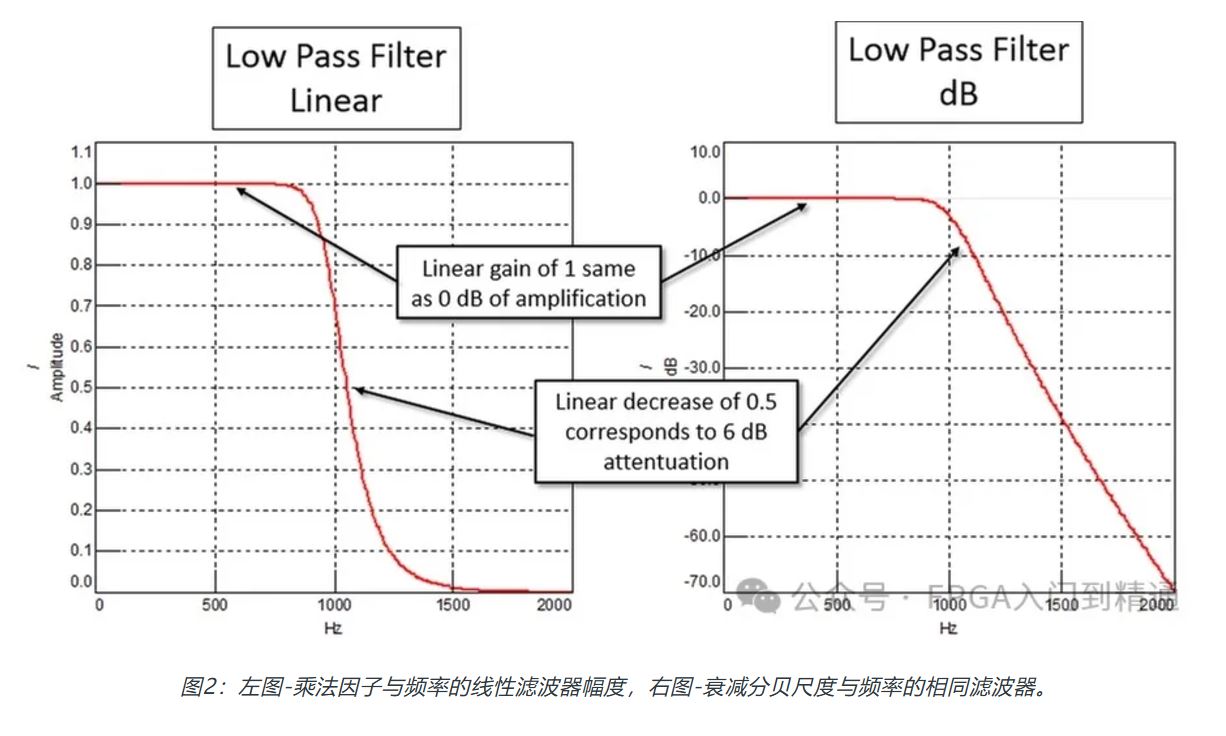
滤波器还可以放大频率内容，而不仅仅是减少或消除它。滤波器调整信号幅度的量可以用线性项（即放大因子）或增益/衰减的分贝表示，如图2所示。
线性振幅减半为6 dB衰减
没有幅度调整对应于1或0 dB衰减的线性增益
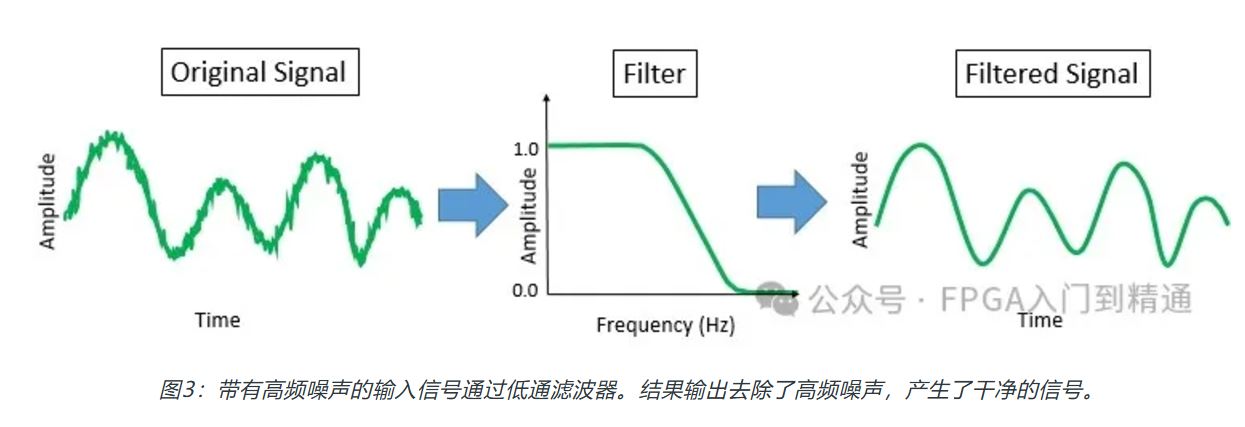
虽然在频域中查看滤波器特性很有用，但滤波器在时域中执行其工作（图3）。
2. 滤波器的应用(Applications of Filters)
滤波器可用于信号清理与信号分析。
在某些应用中，滤波器用于通过衰减不需要的频率内容来调节时域信号，例如：
抗混叠滤波器(Anti-Aliasing Filter)—用于去除模拟数字转换前不能正确数字化的信号频带。
去噪(Noise Removal)—可以用来去除信号中不需要的高频噪声，例如在音乐录音中的呲呲声。
漂移消除(Drift Removal)—通过高通滤波器或交流耦合器(AC coupling)从信号中消除漂移或较大的偏移。
有时滤波器用于将特定的信号特性保留下来用于后续分析:
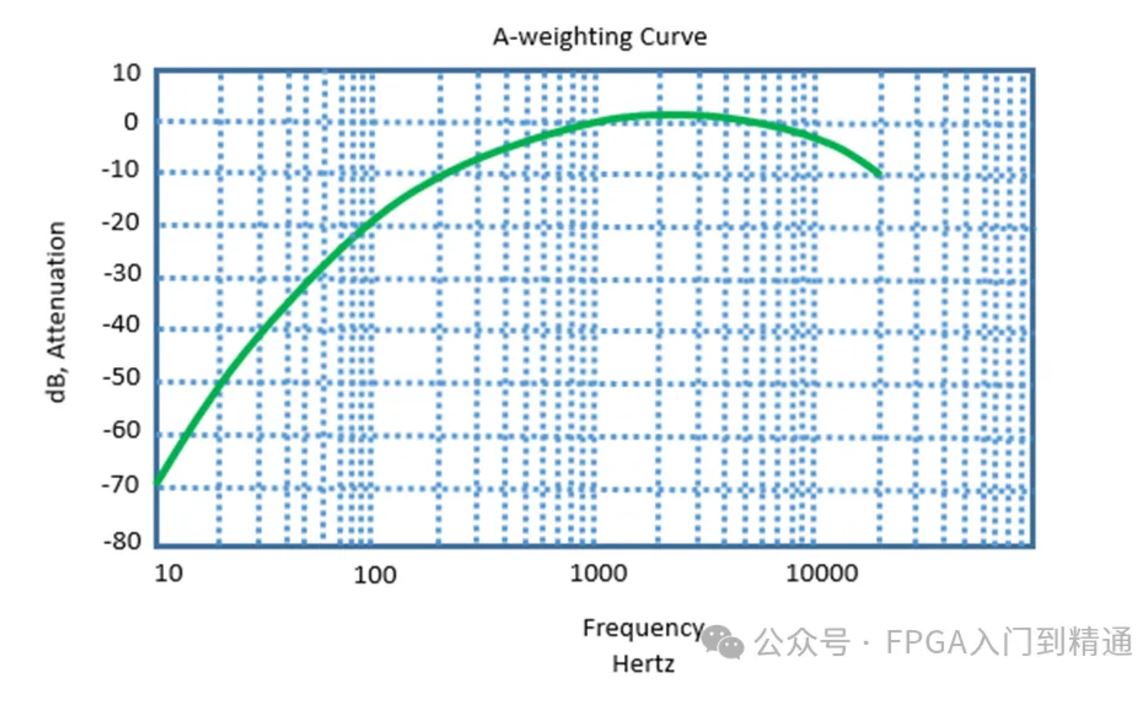
A加权(A-Weighting)—A加权滤波器，用于将人的听觉特性引入麦克风数据采集，如下图所示。麦克风在听不同频率的信号时，其状态是一样的，即无法区分不同的频率输入，而人耳却能感觉到不同频率信号的差异。A加权滤波器降低麦克风采集信号的高频和低频部分，以模拟人耳感知声音的方式。
全身振动加权(Whole Body Vibration Weighting)—人体对某些特定的振动频率比较敏感，因此，基于加速度计的振动信号，结合全身振动加权滤波器(ISO 2631)可以对人体的健康和舒适度进行评价。
滤波器可以在模拟系统（用于实时信号）或数字系统（用于处理PC上已记录的信号）中实现。
3. 滤波器类型(Filter Types)
滤波器可以针对不同的任务进行设计。
例如，滤波器可以分为高通(high pass)、低通(low pass)、带阻(band stop)或带通(band pass)滤波器。
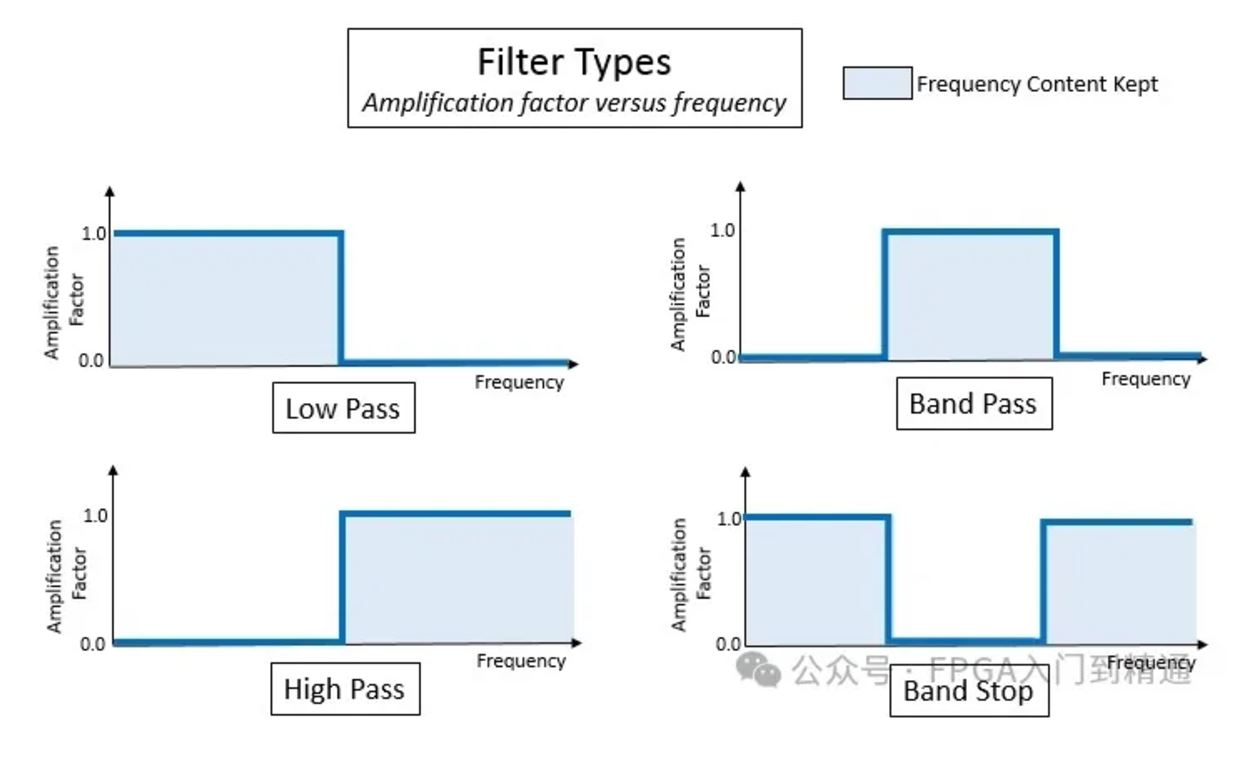
滤波器类型:
高通滤波器—高通滤波器用于去除信号中的低频偏移。例如，如果仅对应变仪信号的动态内容感兴趣，则可以使用高通滤波器去除仪表中的任何低频漂移。
低通滤波器—低通滤波器衰减或消除指定频率以上的频率。例如，其可以用来去除音频记录中的高频嘶嘶声。
带通滤波器—此滤波器用于仅允许指定频率范围内的信号通过滤波器。
带阻滤波器—带阻滤波器用于去除指定范围内的信号频率。
这些滤波器类型可以使用FIR或IIR滤波器来实现, 也可以使用这些组合来生成任意形状的滤波器。
4. FIR和IIR(FIR versus IIR)
两类数字滤波器是有限脉冲响应(Finite Impulse Response, FIR)和无限脉冲响应(Infinite Impulse Response , IIR).
脉冲响应是指滤波器在时域内的出现，滤波器通常具有较宽的频率响应，这对应于时域内的短时间脉冲，如下图所示：
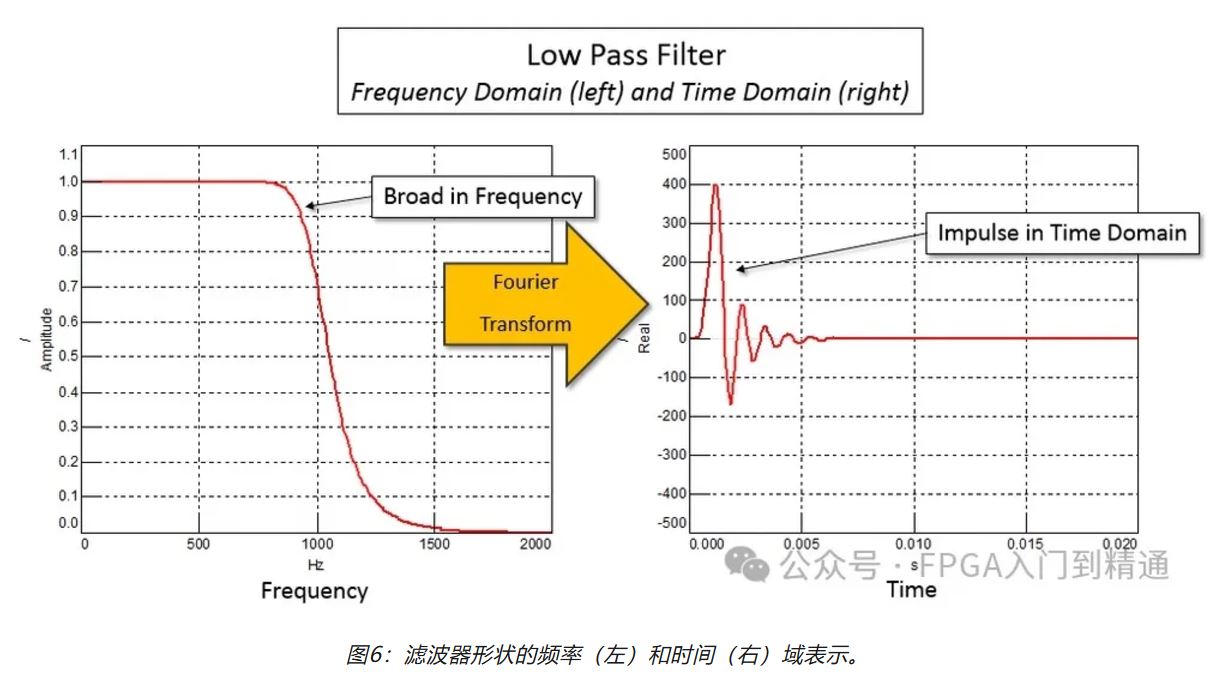
IIR和FIR滤波器的方程如下图所示：
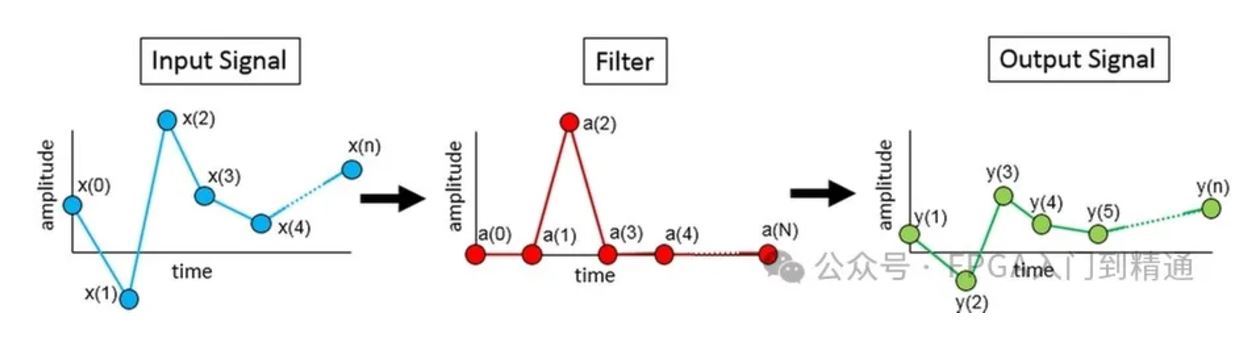
滤波器的输入为时间序列x(n)，滤波器的输出为时间序列y(n)，第一个样本点在n=0处。
每个方程都有三个数字序列: 输入时间序列、滤波器和输出时间序列。
x(n)—输入时间序列是x(0), x(1), x(2), ..., x(n). 小写n是输入时间序列中数据点的总数。
a(k)—FIR滤波器用字符“a” 表示，IIR滤波器用字符“a”和“b”. 大写字母N和P分别表示滤波器中的项数，也称为滤波器的阶数。
y(n)—输出时间序列y(0), y(1), y(2), …
在实践中，FIR和IIR滤波器具有重要的性能差异，如下图所示：
IIR滤波器的优点是，对于与FIR类似的滤波器，可以使用较低的阶数或项数. 这意味着实现相同结果所需的计算量更少，使得IIR的计算速度更快，然而，IIR具有非线性相位和稳定性问题。
这有点像龟兔赛跑的寓言，FIR滤波器就像赛跑中的乌龟—缓慢而稳定，总是能跑完全程。 兔子就像IIR滤波器—非常快，但有时崩溃，并没有完成比赛。
4.1. 滤波器阶数和计算速度(Filter Order and Computational Speed)
由公式中的FIR滤波器方程可知，N越大，滤波器的阶数越高。
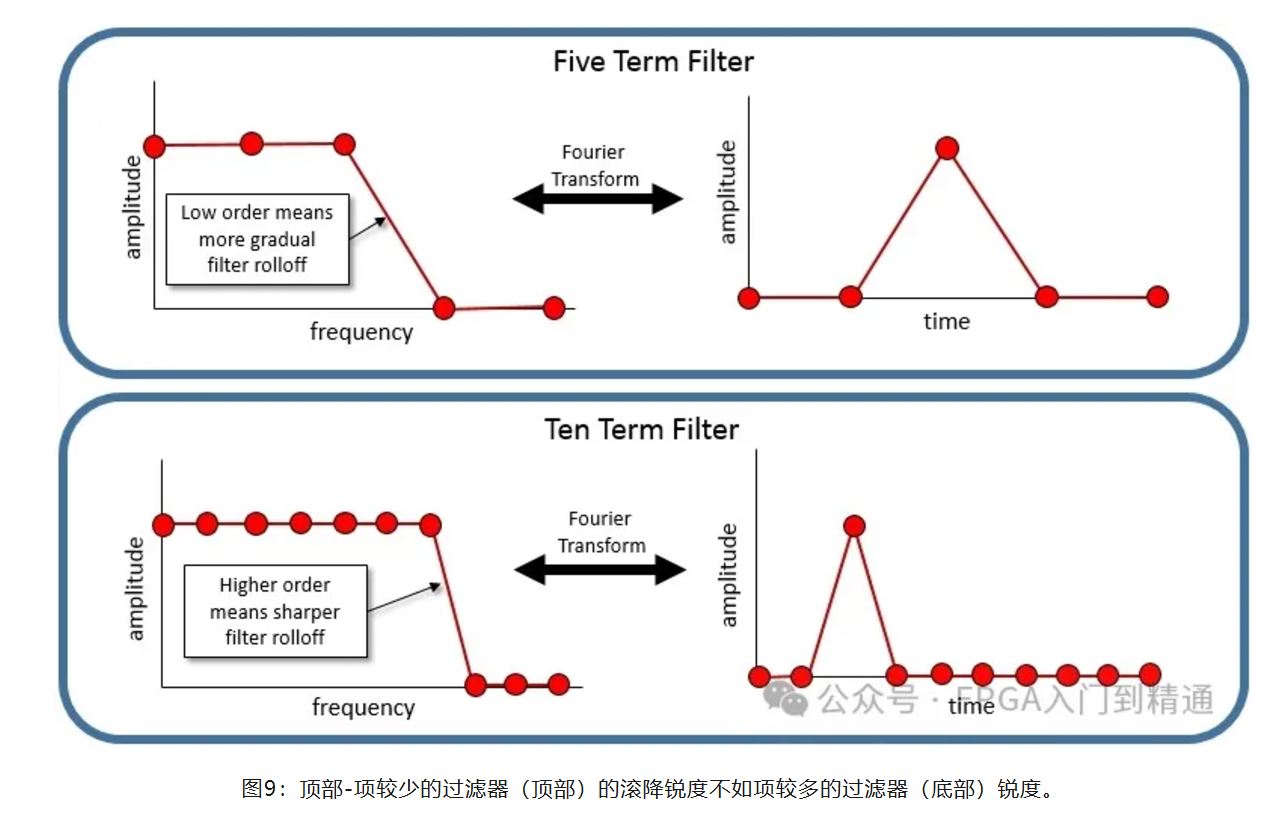
例如，如果滤波器项数为10，而不是5，那么滤波器的计算将花费两倍的时间。然而，滤波器的频率下降会更清晰，如下图所示：
从图中可看出包含更多项(阶数更高)滤波器在通过频率和截止频率之间有更剧烈的转换。
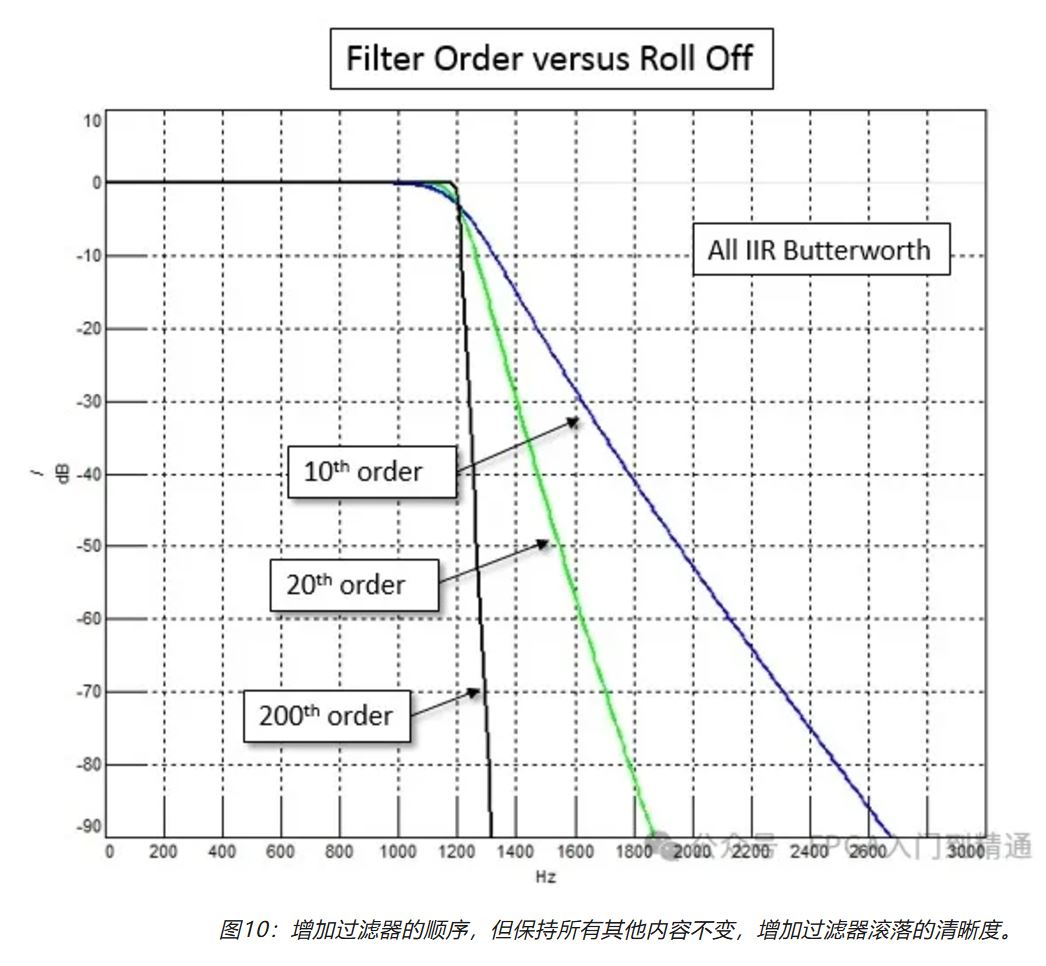
下图显示了相同滤波器类型在使用不同阶数计算时的幅频响应图。
从图中可以看出阶数越高，滤波器的幅频响应变化曲线越陡峭，滤波器对滤除的频率截断效果越显著。
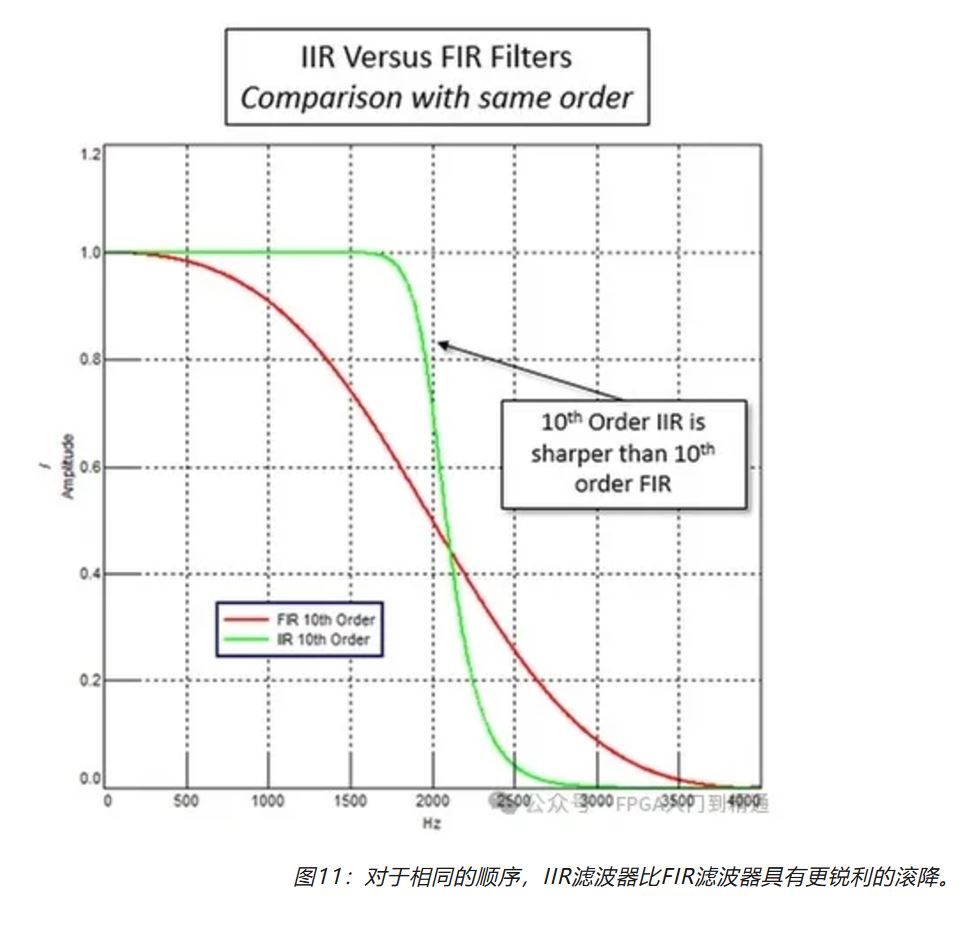
FIR和IIR滤波器的清晰度对于相同的顺序非常不同，如下图所示。由于IIR滤波器的递归性质，其中部分滤波器输出用作输入，它使用相同的顺序滤波器实现了更清晰的滚降。
相反，IIR中可以使用更少的阶数来实现与FIR滤波器相同的性能。这如下图所示。
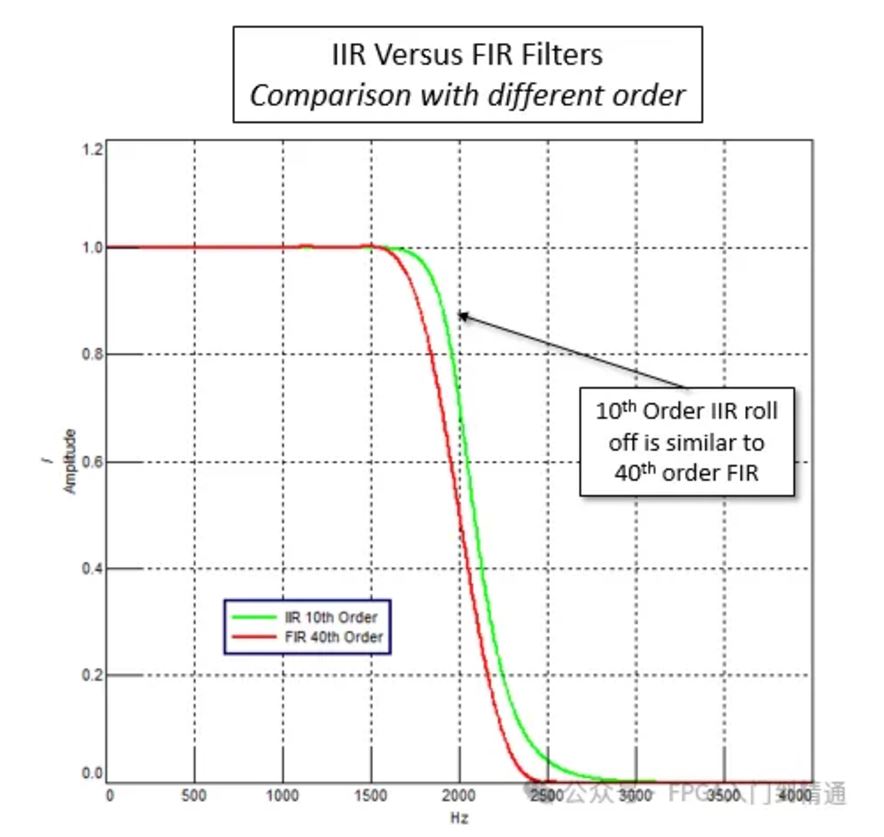
从计算的角度来看，这使得IIR滤波器比FIR滤波器更快。如果过滤器必须在实时应用中实现（例如，监听时的交互式过滤），它通常使用IIR滤波器来完成。
然而，使用IIR滤波器有一些潜在的缺点：
4.2. 滤波器的时间延迟(Time Delay)
滤波后的时间序列，与原始时间序列相比，会出现轻微的偏移或时间延迟。
下图显示了同步采集的声音数据(红色曲线，顶部)和振动数据(蓝色曲线，底部)。
对声音数据滤波器后(绿色曲线，顶部)会导致声音和振动数据之间出现时延现象。
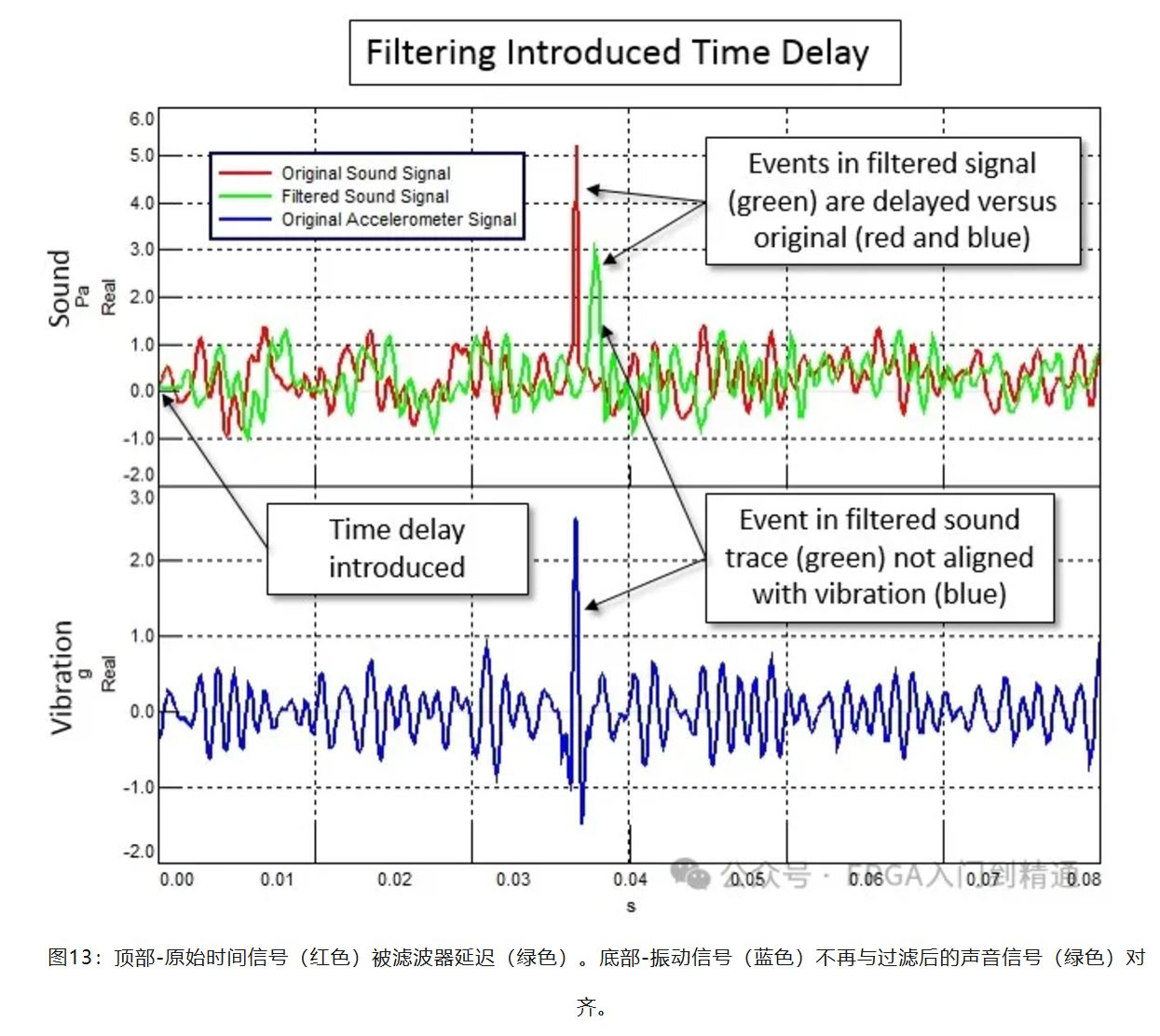
在某些应用程序中，这不是问题，因为偏移量是已知的，可以忽略， 而在其他应用程序中，这种延迟可能很重要。
例如:
什么原因导致滤波器在输出时间序列中引入了时间延迟?
从下图中得到FIR滤波器的方程，通过对该方程的分析，可以看出产生时延的原因。
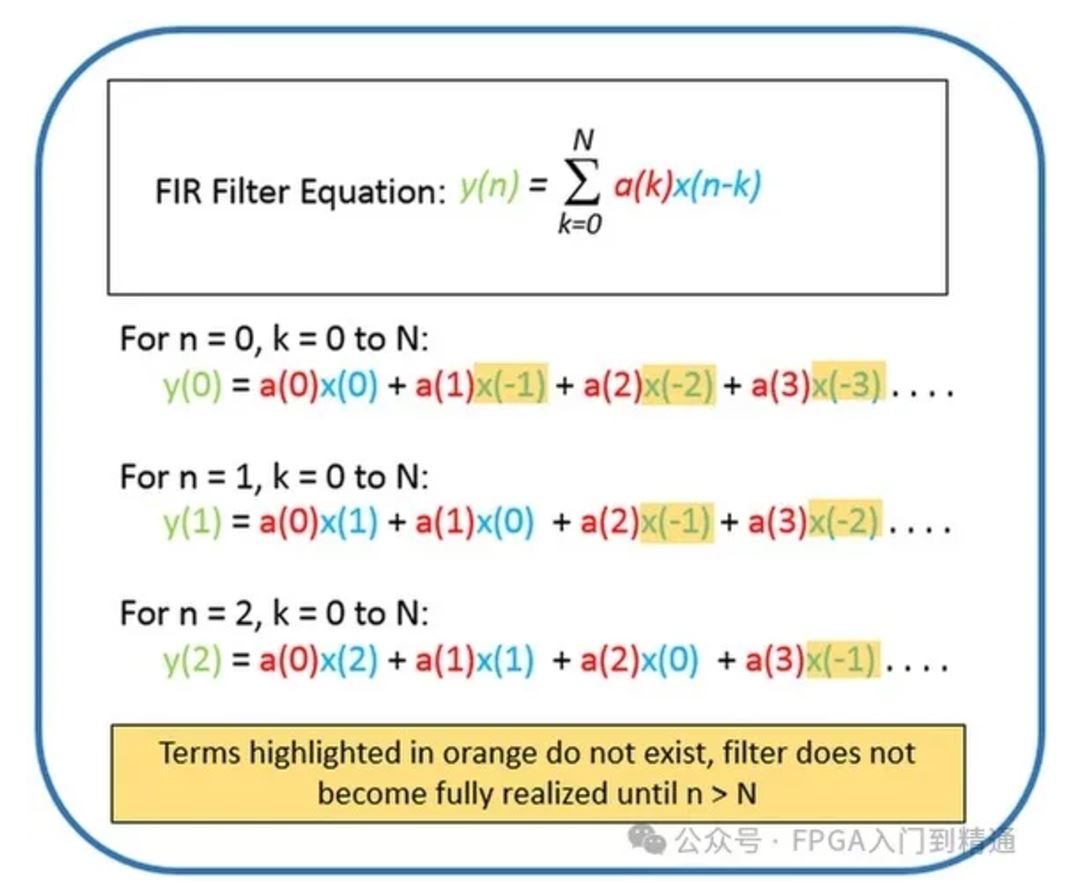
在滤波器工作之前，来自输入信号（x）的时间数据样本的数量必须通过与项数（N）成正比的滤波器。过滤后的输出数据直到通过滤波器的数量（n）数据点大于N才开始。
因为一些数据必须通过过滤器才能创建输出，所以与输入时间历史（x）相比，输出时间历史（y）中的延迟会被创建，如图13所示。通过使过滤器更清晰，这种延迟会增加。
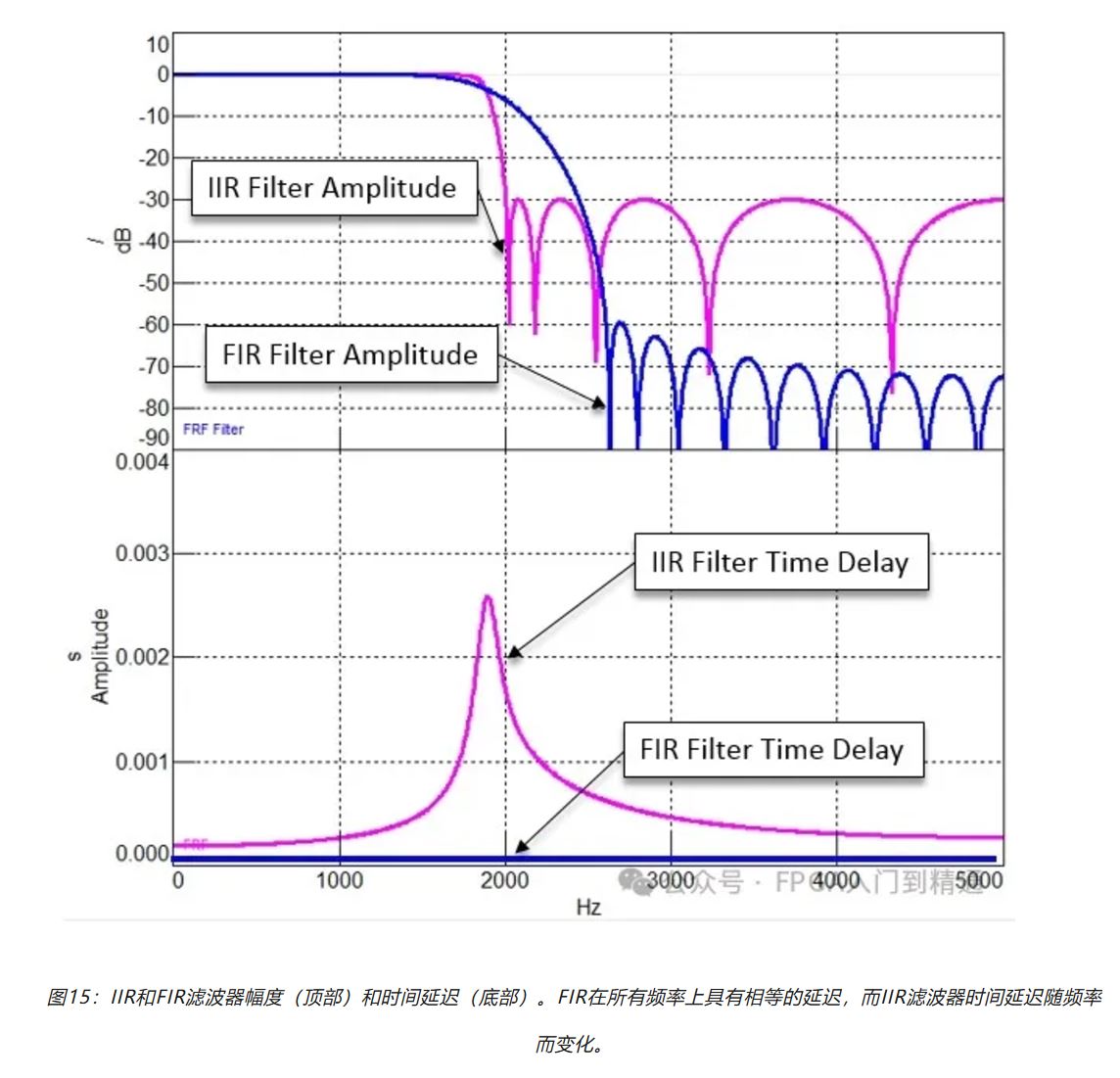
FIR和IIR滤波器的延迟特性非常不同，如图15所示。
从图中可看出，滤波器的幅频响应变化曲线越陡峭锐利，这种延迟就越长。
FIR滤波器在所有频率上具有相同的时延，而IIR滤波器的时延随频率而变化。
所有的滤波器都会产生某种时延(模拟或数字)，根据滤波器的特性，延迟或长或短，它们也可以是频率的函数。
4.3. 零相位滤波(Zero Phase)
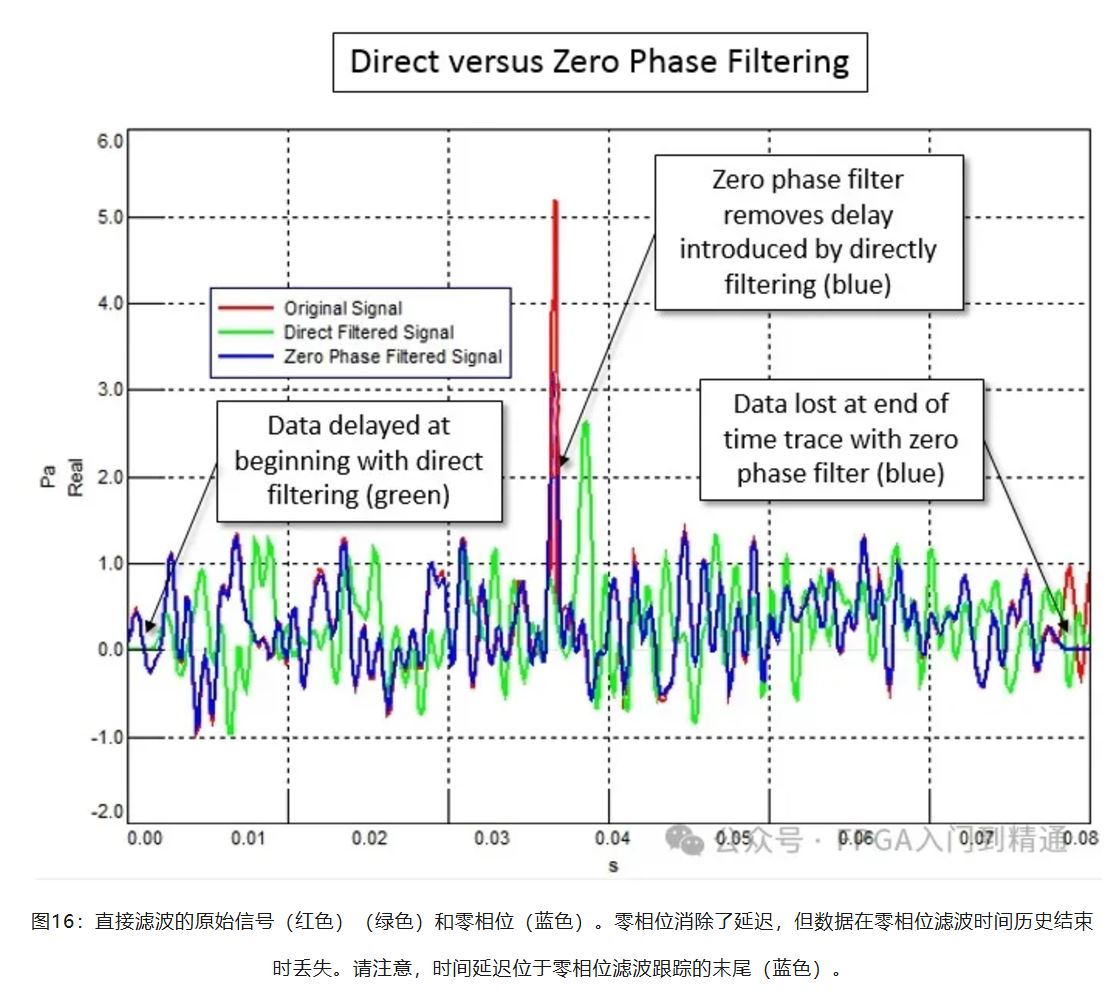
输出时间历史中的延迟可以通过过滤数据'向前和向后'来消除。
时间历史x（n）被过滤后，新的输出时间历史y（n）被创建，它可以被向后馈入滤波器。y（n）中的数据点在时间上按顺序颠倒，并再次馈入滤波器。这被称为“零相位滤波”。结果如图16所示。
“零相位”滤波器时间的输出y（n）不仅与x（n）对齐，但数据被过滤两次，因此衰减加倍。使用零相位滤波器时存在权衡：
5. 滤波器属性(Filter Methods and Attributes)
可以选择过滤器的系数a（n）来控制特定的过滤器属性。系数或方法会影响过滤器属性，如图下图所示。
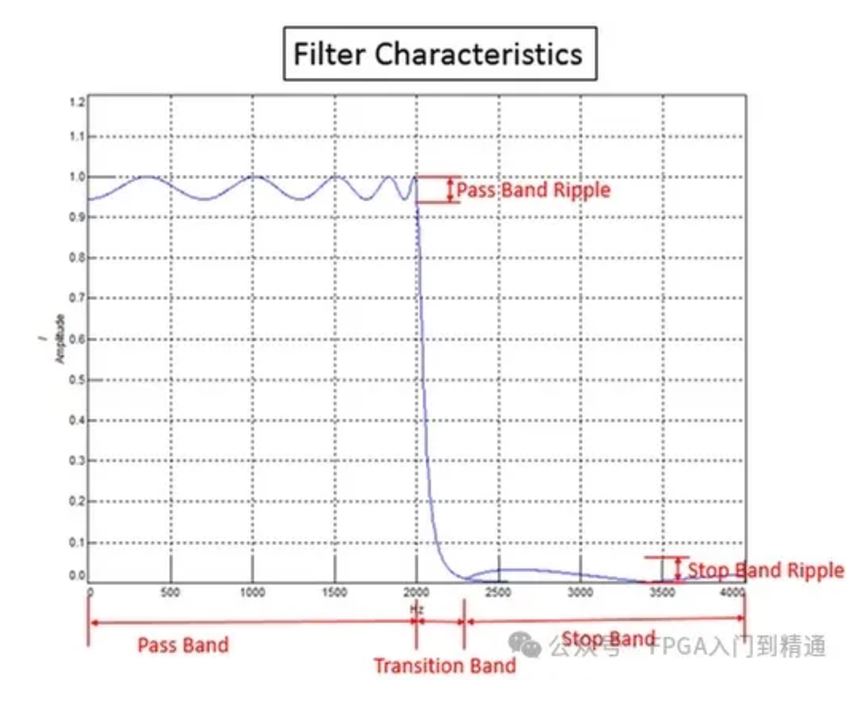
滤波器有四个主要的属性:
（1）通频带(Pass Band)
通带中的数据直接发送到输出时程。为了确保通带中的数据与原始时程数据相同，滤波器中不应有纹波。纹波是幅度随频率的微小变化。理想情况下，在这个频段，滤波器的幅度应该正好为1。
（2）过渡带宽(Transition Width)
根据应用的不同，可能希望通带和截止带之间的过渡在频率方面尽可能窄。方法和滤波器顺序决定了通带和截止带之间的过渡发生的速度。
（3）截止频带(Stop Band)
如果滤波器有纹波，停止带也可以包含数据。在某些应用中，幅度可能很小，没关系。在其他情况下，纹波可能是不可接受的。
（4）组延迟/相位(Group Delay/Phase)
滤波器在输出时间历史中产生延迟，这甚至可以作为频率的函数而变化。如前所述，通过滤波器向前和向后运行时间历史可以消除这种延迟（零相位滤波器）。对于某些应用，相位至关重要，零相位滤波器操作不是一个选项，这可能是一个重要的考虑因素。
5.1 FIR滤波方法(FIR Filter Methods)
下面列出了有限脉冲响应(FIR)滤波器的方法：
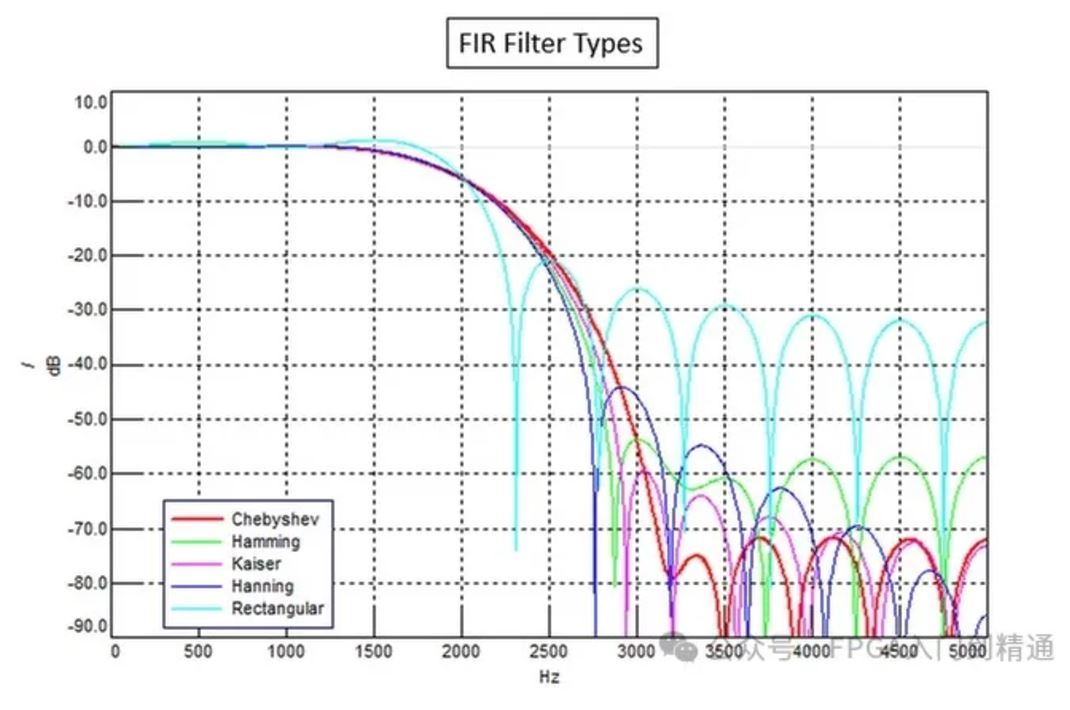
FIR方法在从频域到时域的转换中使用了不同的谱窗。
常用的窗口方法包括:
（1）切比雪夫（Chebyshev）
停止带纹波最小，过渡带最宽。
（2）汉明（Hamming）
狭窄的过渡区，波纹比汉宁小。由曼哈顿计划成员理查德·汉明开发。
（3）凯泽（Kaiser ）
由贝尔实验室的詹姆斯·凯泽开发，凯泽窗口在停止区具有小幅度波纹，只有宽过渡宽度切比雪夫具有较低的幅度波纹。
（4）汉宁（Hanning）
过渡带最窄，停止带纹波较大。
（5）矩形（Rectangular ）
纹波最大，甚至影响通带。
5.2 IIR滤波方法(IIR Filter Methods)
无限脉冲响应滤波器的方法：
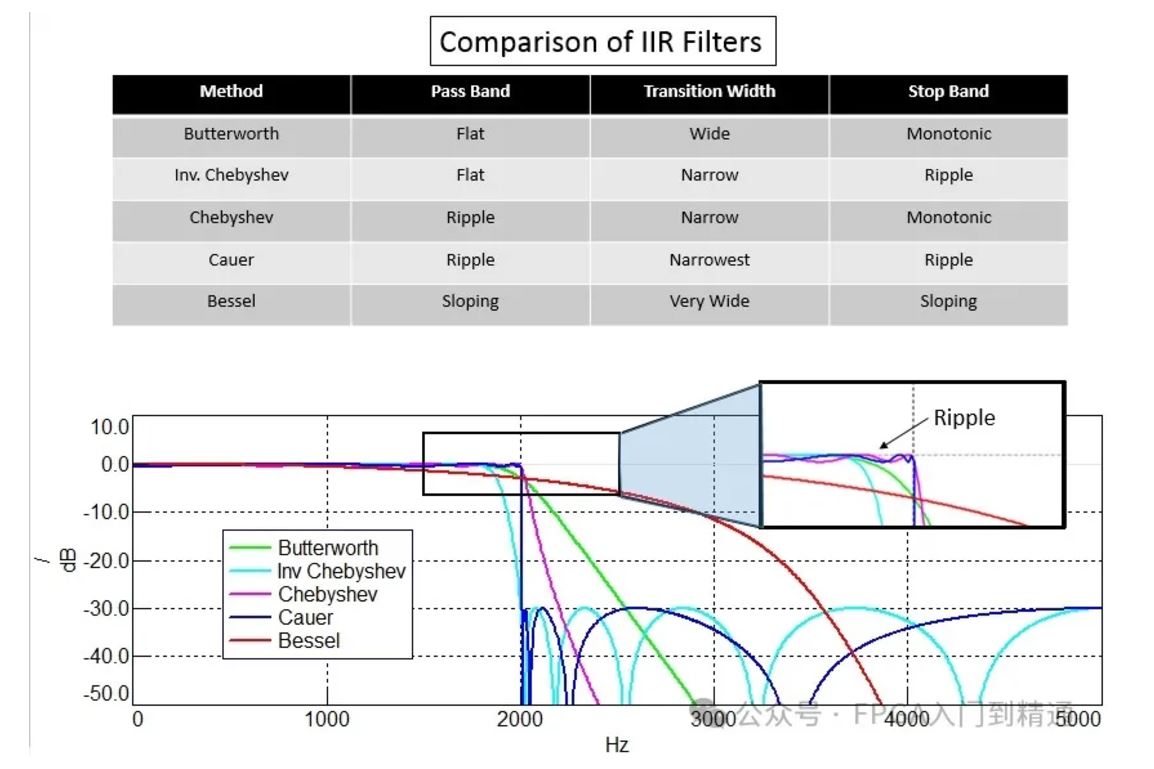
不同IIR滤波方法的属性:
（1）巴特沃斯 （Butterworth）
通过带和停止带的平坦响应，但有一个宽的过渡区。英国物理学家斯蒂芬·巴特沃斯于1930年首次描述。
（2）逆切比雪夫 （Inverse Chebyshev）
通带平坦，过渡宽度比巴特沃斯滤波器窄，但在截止带有纹波。
如果截止带的纹波不是问题，对于给定的应用，可能比巴特沃斯滤波器更受欢迎。
（3）切比雪夫 （Chebyshev）
通带可以有波纹，但比反切比雪夫有更陡的滚落。
（4）Cauer
最窄的过渡区。停止和通过带中的纹波。有时称为椭圆滤波器。
（5）贝塞尔（Bessel ）
通带和阻带的斜率幅度，过渡带非常宽。滤波器中的延迟对频率是这个列表中最平坦的。贝塞尔滤波器以德国数学家弗里德里希·贝塞尔（1784-1846）的名字命名。
