作者:威视锐科技
DSP基础
3.1采样
将模拟信号转换为数字等效信号时发生的两个过程分别是采样和量化。可以将采样视为将信号的时间轴转换为一组离散时刻,而量化则将其振幅转换为一系列离散的可表示振幅值。这种简单的模数转换模型如图3.1所示。
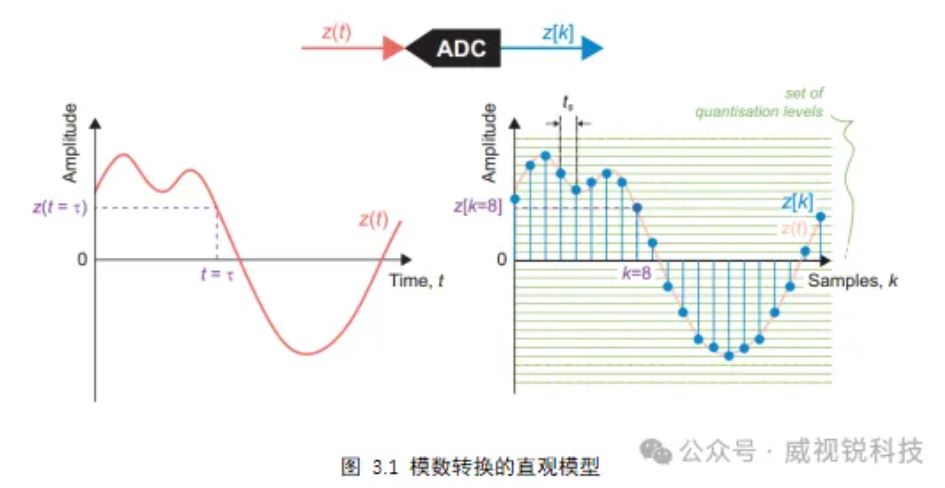
如图3.1左侧所示,模拟信号被视为连续时间,这意味着振幅是在所有时间内定义的。当转换到数字域时,如图3.1右侧所示,信号被表示为离散的时刻,这些时刻被采样周期分开。这种转换过程称为采样。采样周期和采样频率具有倒数关系,如(3.1)所示。
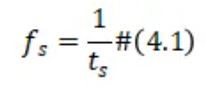
3.1.1 采样率选择
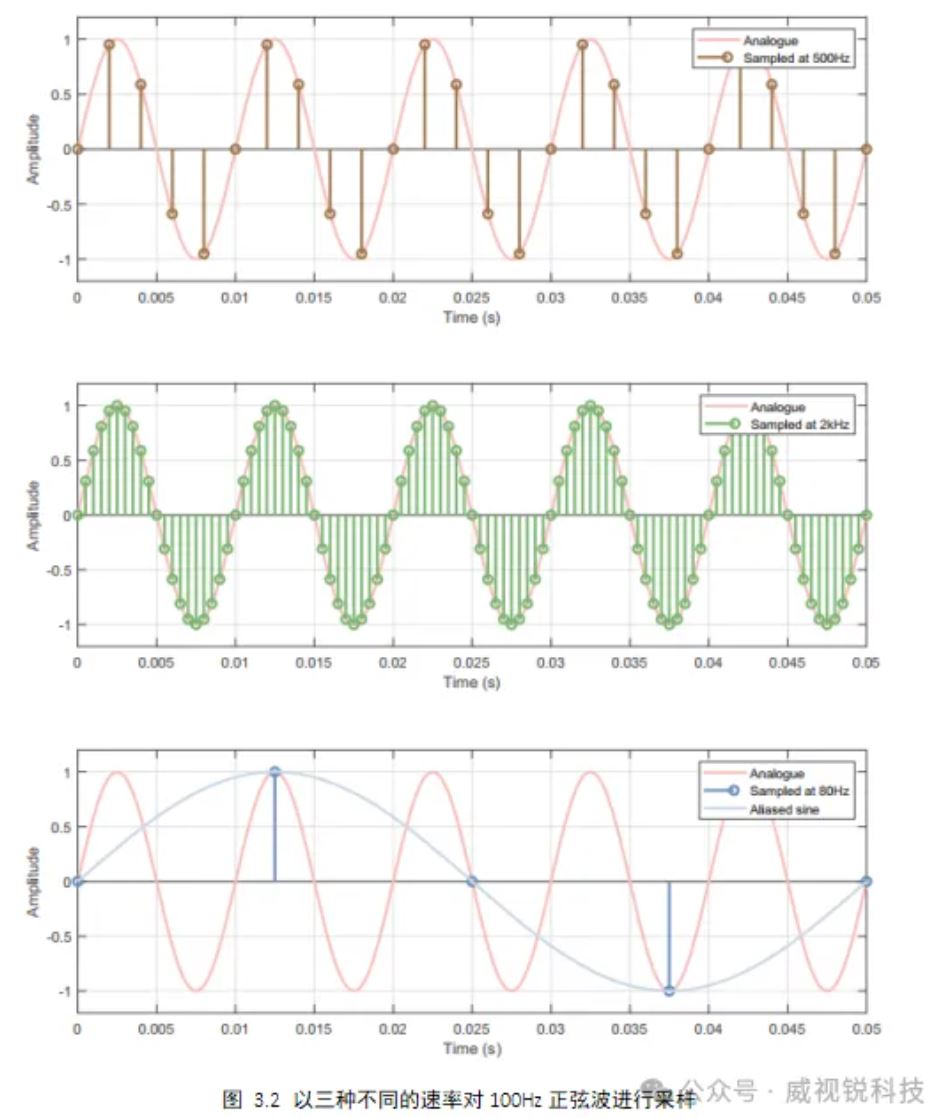
适当采样频率的选择主要受待处理信号的频率内容的影响。采样过慢,则无法正确捕获有关信号的信息,采样过快,处理信号所需的操作则被不必要地夸大。图3.2中展示了以三种不同速率采样的100Hz正弦波。
过高的采样率可以可靠地捕获信号,但也会为后续处理带来许多不必要的开销。过低的采样率会导致正弦波不能从以该速率采集的样本中准确地重建。图中以80Hz的速率采样,实际上会得到更低频率的正弦波,这种效果通常被成为混叠。当前例子中混叠信号的频率为20Hz,这与正弦波频率和采样率有关,如:
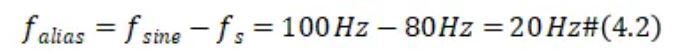
尽管混叠通常被认为是一种不可取的效果,但在某些情况下,它可能会被故意利用,这将在后面讨论。
3.1.2 信号频率范围术语
图3.3展示了两个信号在频域上的草图
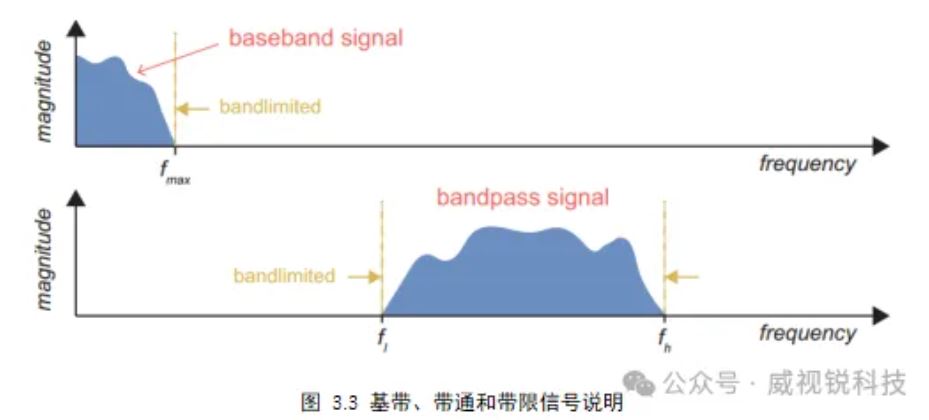
首先,当信号的最低频率分量处于或接近0Hz时,该信号被称为基带。通常在通信中,我们考虑的信号分别处于发射机或接收机调制或解调的过程中,不具有任何接近0Hz的分量,可以用带通描述这些信号,反映出信号占用的频率范围不接近0Hz。基带和带通信号也可以被称为带限信号,这意味着信号能量被包含在特定的频率范围内。
3.1.3 奈奎斯特采样定理
为了避免混叠,奈奎斯特采样定理给出了最小可能采样频率的更正式的定义。奈奎斯特采样定理指出,基带带限信号的采样频率必须大于信号中最大频率分量的两倍,即

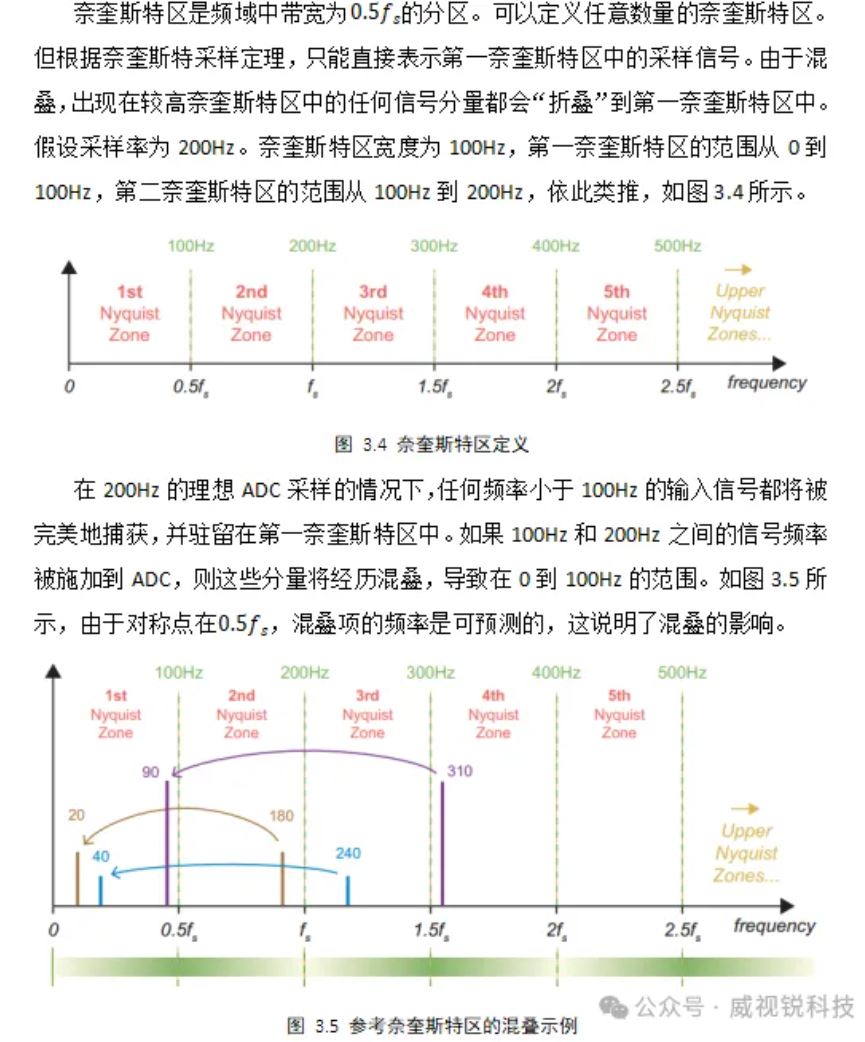
3.1.4 奈奎斯特区和混叠
欠采样技术可用于利用混叠,并有意将带通信号向下折叠到奈奎斯特一区。该技术可以在接收机中用作将IF或RF调制信号转换为基带的手段,也就是下变频。该技术的一个示例如图3.6的上半部分所示,颜色为紫色。下变频信号的主要优点之一是后续处理阶段所需的采样率可以显著降低,这可以减少功耗和计算负载。该技术依赖于原始信号完全包含在单个奈奎斯特区中,否则产生的频谱会被混叠分量的叠加破坏,如图3.6的下半部分所示。注意,当接收到的信号跨越两个奈奎斯特区时,信号的两个单独部分都混叠到第一奈奎斯特区的上部,并且彼此叠加。
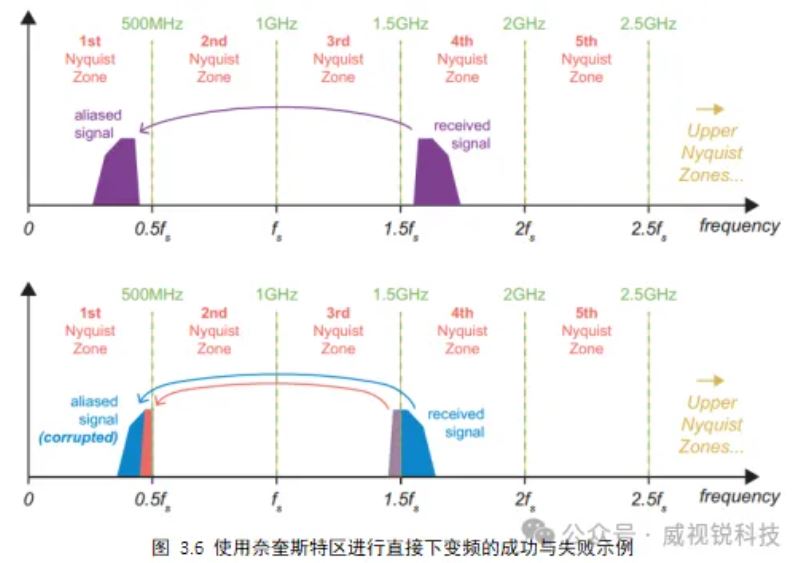
这些例子没有考虑频谱中存在的任何其他频率分量。然而,在使用这种方法进行下变频之前,也应谨慎地对信号进行带通滤波。这将去除任何其他奈奎斯特区中存在的任何噪声或杂散频率分量,否则所有这些分量都将混叠到第一奈奎斯特区并降低所需信号的质量。
RFSoC器件在其RF-ADC处理中利用奈奎斯特区进行信号接收;在发射侧,使用RFSoC的RF-DAC在上部奈奎斯特区生成信号。
3.1.5 采样抖动 实际情况中,ADC的采样的预期样本之间的周期会有一些变化,如图3.7所示。

可变采样周期的这种影响被称为抖动,这是我们不希望看到的,因为输入信号的采样不是在理想的时刻进行的。抖动也是DAC的一个特性,其中期望的输出样本在采样周期中受到误差的影响,因此不能在正确的时刻产生。与理想采样时刻相比,由于采样在时间上错位,振幅值经历相应的误差。所以抖动可以被建模为噪声源。
高保真度DAC和ADC在很大程度上最大限度地减少了抖动,然而在非常高的采样频率下,抖动可能是一个显著的问题。
文章来源:威视锐科技