文章来源:FPGA入门到精通
前面两篇文章详细介绍了DFT和FFT,今天介绍一下使用Verilog实现8点FFT。
3分钟掌握离散傅里叶变换(DFT):数字世界的“频率解码器”
快速傅里叶变换(FFT):从数学公式到5G信号,揭开数字世界的“频率密码”
8 点 FFT 计算的结构示意图如下:
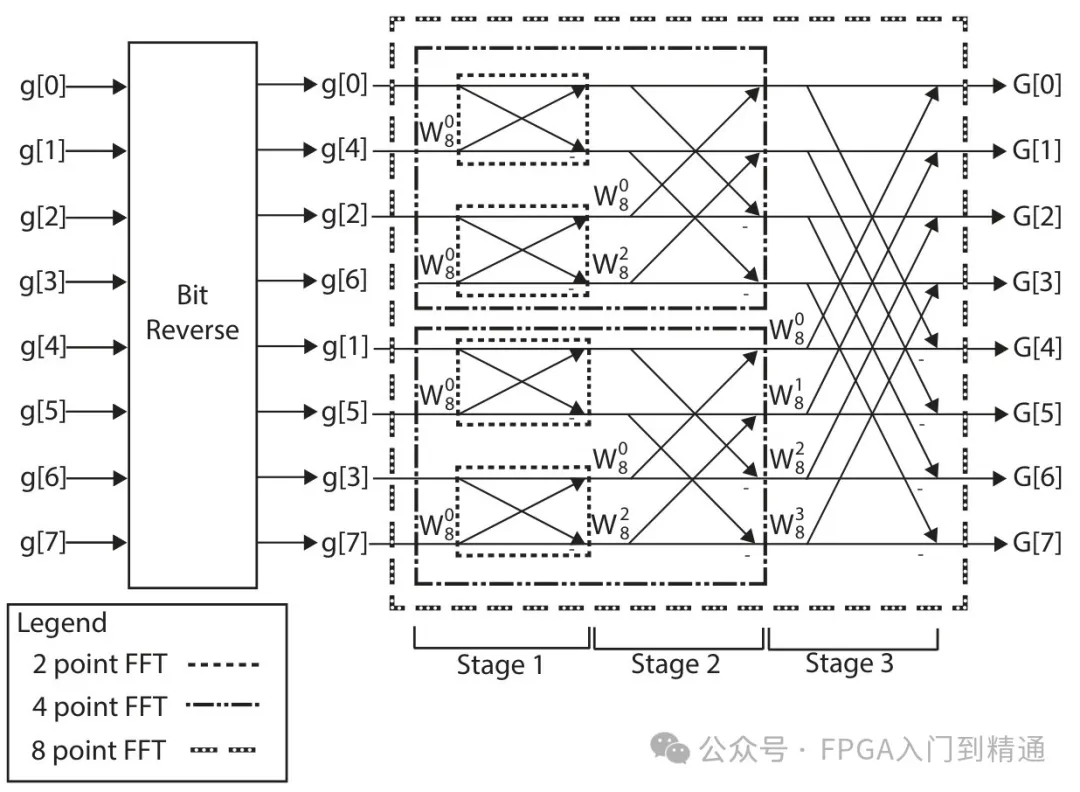
从图中可以看出8点FFT计算只需要几次乘法和乘法即可完成,比繁琐的DFT计算简单很多。
1、复数数据格式
每一级的数据输入都是复数,包含实部和虚部,对于第一级输入的时域信号数据是实数,只需将虚部设为0即可。
2、分级运算 “ 如何理解 ” ?
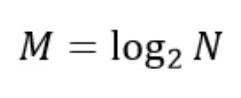
8点FFT运算可以分为Log28 = 3级运算。
每一级运算,一般用m表示第几级,m = 1, ..., M。
为了方便分割计算,N 一般为 2 的整数次幂。
3、蝶形运算单元
每一级运算可以分为多个蝶形运算单元。
单个蝶形运算示意图如下:
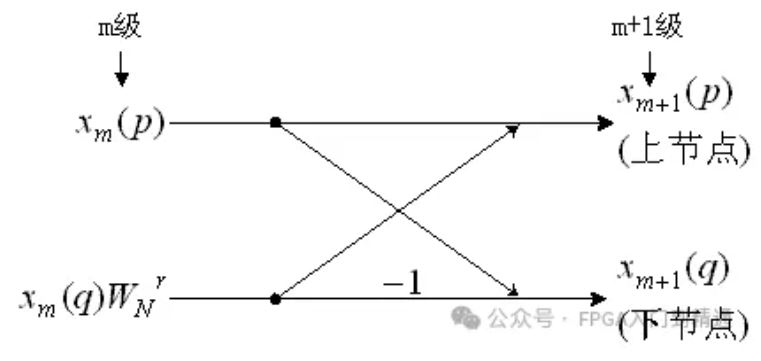
单个蝶形运算单元计算公式为:
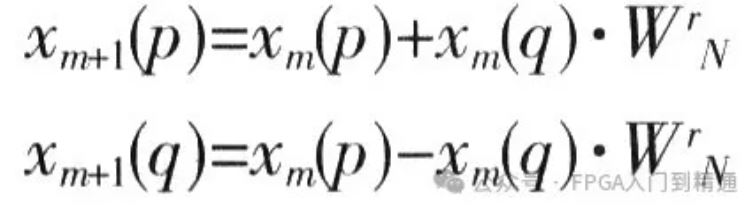
其中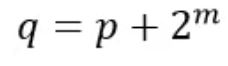 ,m表示第几级数。
,m表示第几级数。
从公式中可以看出,每个蝶形单元运算都包含了“1次乘法”和“2次加法”。
每一级运算中,都有 N/2 个蝶形单元。
4、每一级运算分组 “ 如何理解 ” ?
(1)分组的层级性
第 ( m ) 级的分组数:
对于 ( N = 2^M ) 点FFT,在第 ( m ) 级(( m=1,2,...,M ))时,数据被分为 2^m组。
每组内的数据通过蝶形运算合并结果,每组需要完成 ( 2^{m-1} ) 次蝶形运算。
(2)分组的物理意义
递归分解:每一级的分组将问题规模减半,直到分解为2点DFT(最底层蝶形运算)。
4、旋转因子与分级的关系

每一级的旋转因子指数按k = 0,△k,2△k,...,(N/2^m - 1)△k增长。
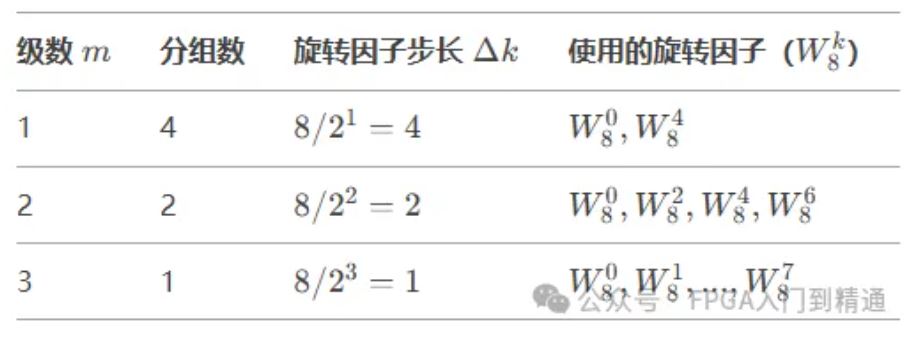
5、码位倒置
以8点FFT为例,X(0) ~ X(7) 位置对应的 2 进制码:
X(000), X(001), X(010), X(011), X(100), X(101), X(110), X(111)
进行翻转:
X(000), X(100), X(010), X(110), X(001), X(101), X(011), X(111)
此时每个位置对应的 10 进制:
X(0), X(4), X(2), X(6), X(1), X(5), X(3), X(7)
刚好对应 FFT 第一级输入数据的顺序。