作者:张海军,来源:傅里叶的猫
好久没写跟信号处理相关的内容了,我们这个公众号名字“傅里叶的猫”也是因为笔者是信号处理专业出身,刚工作的前几年一直在做跟信号处理相关的工作。
最近有小伙伴问我,有没有用Python做信号处理的入门教程,这位小伙伴本身的工作跟信号处理有关,又想学一下Python相关的东西。也许有同学会问,用Matlab多方便,为什么还要再用Python来做?其实现在Python的库非常丰富了,做信号处理仿真的能力也是非常强的,而且用Python仿真完后,如果需要再翻译成C++工程代码,也是要更方便的。再者,技多不压身,多学一门技能对我们日后跳槽或者职业发展都是有帮助的。
这篇文章我们介绍如何使用Python进行频率分析、噪声滤波和幅度谱提取。
1. 基础理论
我们先来回顾一下信号处理中的几个基础理论。
1.1 傅里叶变换
一个一维信号不过是一系列的时间数据点,这意味着有一个横轴,代表时间,以及一个纵轴,代表我们考虑的量(例如电压)。
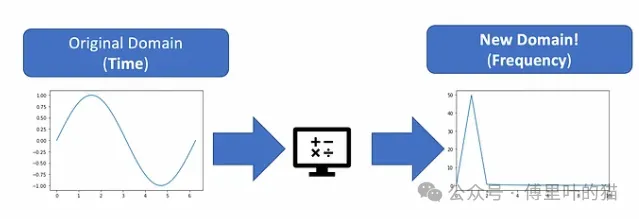
从直观的角度来看,对一个信号进行傅里叶变换意味着在这个信号的另一个域中观察它,其核心思想是从时间域转到频率域来观察信号。
在时间域中,信号是一系列随时间变化的值。然而,在频率域中,同一个信号被表示为其不同频率分量的组合。傅里叶变换帮助我们将信号分解成一系列不同频率的正弦波,每个正弦波都有自己的振幅和相位。
通过这种方式,我们可以更好地理解信号中包含的频率信息,这对于诸如滤波、去噪和特征提取等任务非常有用。在频率域中,某些信号处理任务会变得更加直观和简单。例如,去除噪声可以通过简单的滤波器实现,该滤波器会抑制或增强某些频率范围内的信号分量。
1.2 小波变换
下面我们看一个比正弦函数更复杂的信号,比如下面所示:

小波变换是一种局部化的变换,它允许我们在时间和频率两个维度上同时分析信号。与傅里叶变换相比,小波变换的一个关键优势在于它可以捕捉信号的局部特性,而不仅仅是全局特征。这意味着对于非平稳信号(即信号的统计属性随时间变化的情况),小波变换可以提供有价值的信息。
1.3 希尔伯特变换
有些信号虽然上下波动,但我们并不关心这些细节,只想获取信号的包络线。数学上,这一操作是通过卷积来完成的。我们下面会具体说明。
2. 实际例程
先导入我们需要的库:
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from scipy import signal
import pywt
2.1 数据预处理
data_fft = pd.read_csv('AEP_hourly.csv')
y = np.array(data_fft.AEP_MW)
x = data_fft.index
date_array = pd.to_datetime(data_fft.Datetime)
plt.plot(date_array,y)
plt.xlabel('Date',fontsize=20)
plt.ylabel('MW Energy Consumption',fontsize=20)
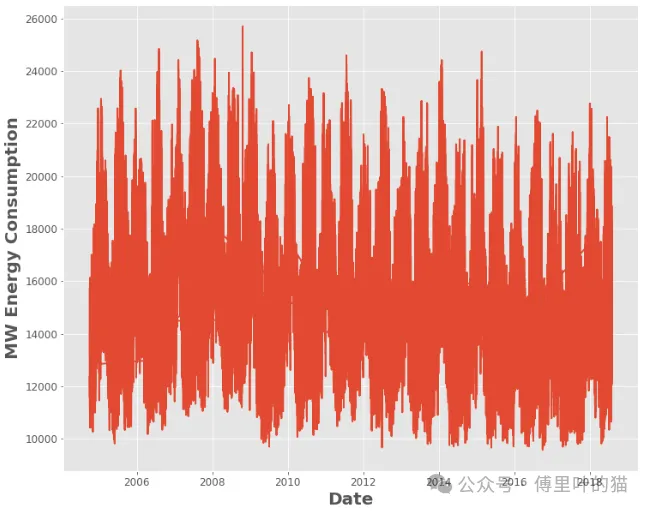
为了消除趋势并确保信号的均值接近于零,我们可以使用scipy库中的detrend函数来处理这个问题。detrend函数可以帮助我们去除信号中的线性或常数趋势,从而让我们专注于信号的其他特征。
y_detrend = signal.detrend(y)
plt.plot(date_array, y_detrend,color='firebrick',label='Detrended Signal')
plt.plot(date_array,y, color='navy',label='Raw Signal')
plt.legend()
plt.xlabel('Date',fontsize=20)
plt.ylabel('Temperature',fontsize=20)

2.2 频率分析
我们来看下FFT结果:
FFT =np.fft.fft(y_detrend)
new_N=int(len(FFT)/2)
f_nat=1
new_X = np.linspace(10**-12, f_nat/2, new_N, endpoint=True)
new_Xph=1.0/(new_X)
FFT_abs=np.abs(FFT)
plt.plot(new_Xph,2*FFT_abs[0:int(len(FFT)/2.)]/len(new_Xph),color='black')
plt.xlabel('Period ($h$)',fontsize=20)
plt.ylabel('Amplitude',fontsize=20)
plt.title('(Fast) Fourier Transform Method Algorithm',fontsize=20)
plt.grid(True)
plt.xlim(0,200)
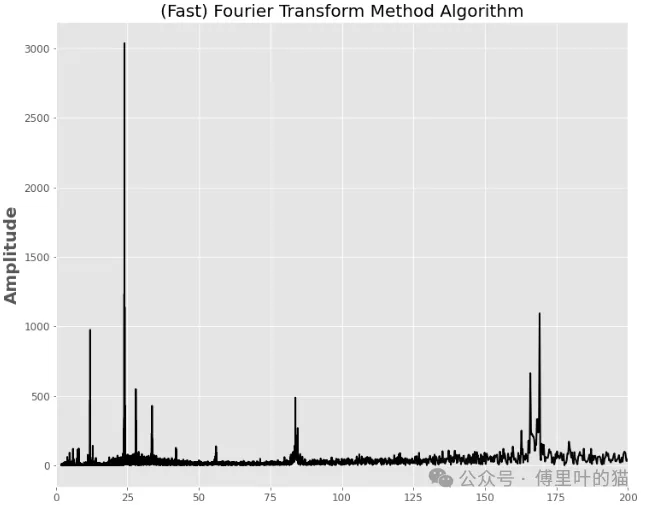
我们可以把峰值结果取出来:
fft_abs = 2*FFT_abs[0:int(len(FFT)/2.)]/len(new_Xph)
fft_abs = pd.DataFrame(fft_abs, columns = ['Amplitude'])
fft_sorted = fft_abs.sort_values(by='Amplitude',ascending=False).head(20)
2.3 噪声滤波
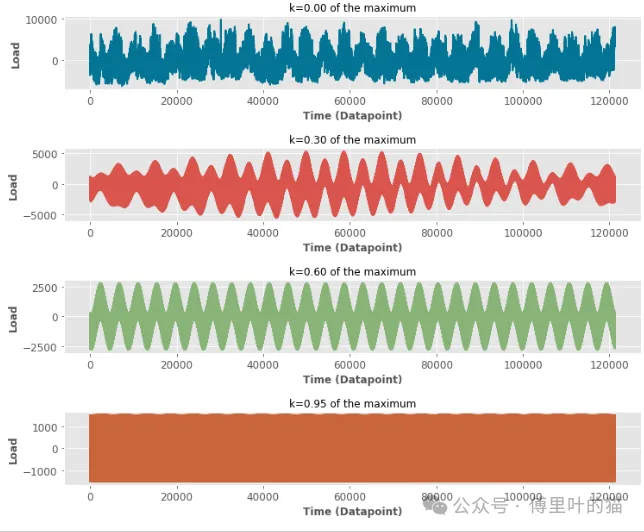
现在我们可以将最高的峰作为参考,并开始滤除低于最高峰0.1、0.2……0.9的峰。例如,我们可以将低于最高峰幅度0.5倍的所有值设为零。
如果设定的阈值太高,我们不仅会滤除噪声,还会滤除信号的重要特征。如果阈值太低,那么基本上不会滤除任何东西,仍然保留所有的噪声。
#Defining the filtering function
def fft_filter(th):
fft_tof=FFT.copy()
fft_tof_abs=np.abs(fft_tof)
fft_tof_abs=2*fft_tof_abs/len(new_Xph)
fft_tof[fft_tof_abs<=th]=0
return fft_tof
#Showing the plots at different thresholds values
#Defining the amplitude filtering function
def fft_filter_amp(th):
fft_tof=FFT.copy()
fft_tof_abs=np.abs(fft_tof)
fft_tof_abs=2*fft_tof_abs/len(new_Xph)
fft_tof_abs[fft_tof_abs<=th]=0
return fft_tof_abs[0:int(len(fft_tof_abs)/2.)]
K_plot=[10,200,700,1500]
j=0
for k in K_plot:
j=j+1
plt.subplot(2,2,j)
plt.title('k=%i'%(k))
plt.xlim(0,200)
plt.plot(new_Xph,2*FFT_abs[0:int(len(FFT)/2.)]/len(new_Xph),color='navy',alpha=0.5,label='Original')
plt.grid(True)
plt.plot(new_Xph,fft_filter_amp(k),'red',label='Filtered')
plt.xlabel('Time($h$)')
plt.ylabel('Amplitude')
plt.legend()
plt.subplots_adjust(hspace=0.5)
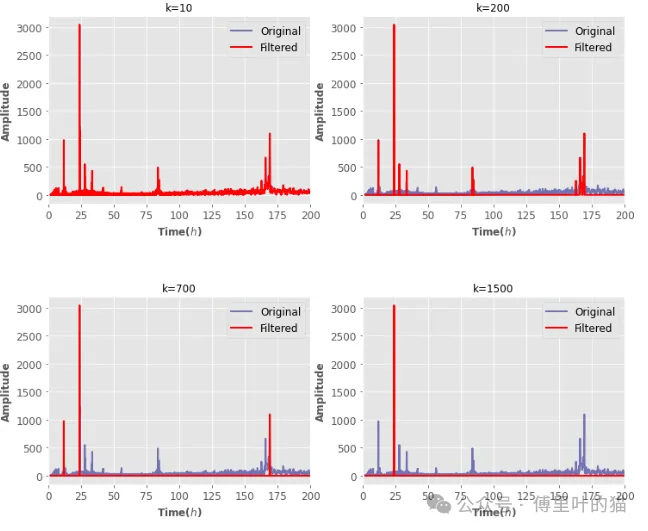
用下面代码看下结果:
def fft_filter(perc):
th=perc*(2*FFT_abs[0:int(len(FFT)/2.)]/len(new_Xph)).max()
fft_tof=FFT.copy()
fft_tof_abs=np.abs(fft_tof)
fft_tof_abs=2*fft_tof_abs/len(new_Xph)
fft_tof[fft_tof_abs<=th]=0
return fft_tof
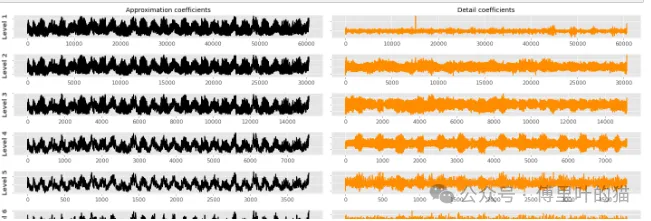
2.4 基于小波变换的滤波
我们也可以使用小波变换来进行噪声滤波。在这种情况下,我们有多级滤波,最初的几级只会滤除纯噪声,但它们会比较保守。深入得越多,残留的噪声就越少,但同时也会丢失信号的特征(残留信号将类似于原始信号)。
time=x.max()
sample_rate=1/900.
size= int(sample_rate*time)
t = np.linspace(0, time, num=size)
dataset = y_detrend
waveletname = 'sym2'
levels=8
fig, axarr = plt.subplots(nrows=levels, ncols=2, figsize=(20,10))
COEFF_D=[]
DATASET=[]
k=1
for ii in range(levels):
(dataset, coeff_d) = pywt.dwt(dataset, waveletname,mode='per')
axarr[ii, 0].plot(dataset, 'black')
axarr[ii, 1].plot(coeff_d, 'darkorange')
axarr[ii, 0].set_ylabel("Level {}".format(ii + 1), fontsize=14, rotation=90)
axarr[ii, 0].set_yticklabels([])
if ii == 0:
axarr[ii, 0].set_title("Approximation coefficients", fontsize=14)
axarr[ii, 1].set_title("Detail coefficients", fontsize=14)
axarr[ii, 1].set_yticklabels([])
#print(len(coeff_d))
COEFF_D.append(np.repeat(coeff_d,2**k))
DATASET.append(np.repeat(dataset,2**k))
k=k+1
plt.tight_layout()
plt.show()
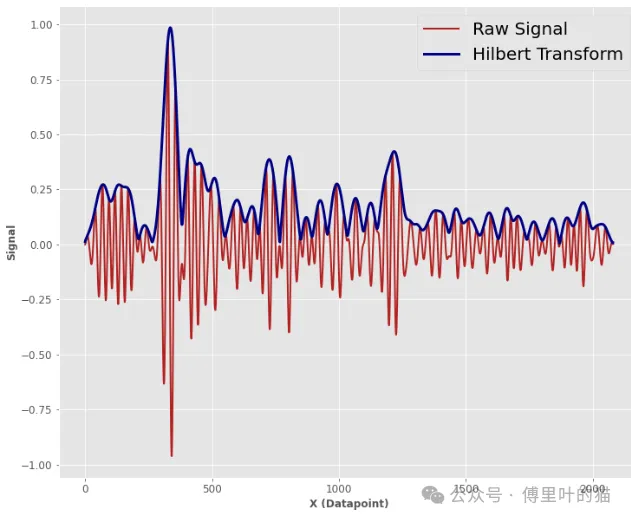
2.5 包络提取
在这个部分,我们只是构造了一个起伏的信号,要提取它的包络,只需应用scipy的希尔伯特变换并计算绝对值即可:
new_data = pd.read_csv('shiftedsignaltest20.csv').drop('Unnamed: 0',axis=1)
new_signal = np.array(new_data.loc[0])
plt.plot(new_signal,color='firebrick',label='Raw Signal')
plt.xlabel('X (Datapoint)')
plt.ylabel('Signal')
plt.plot(np.abs(hilbert(new_signal)),color='navy',lw=3,label='Hilbert Transform')
plt.legend(fontsize=20)
内容参考自:
